в каком квадрате находится особый объект то есть не такой как остальные
Логический квадрат в логике
Ежедневно каждый человек выполняет действия, направленные на решение логических задач. В простом понимании логика выражается в способностях мыслить и рассуждать последовательно, чтобы не противоречить самому себе. И такой навык необходим не только при проведении бизнес-переговоров с деловыми партнерами, а и для совершения покупки на рынке или в магазине.
Многие люди, логические навыки которых далеки от совершенства, часто совершают логические ошибки, не замечая этого. Большинство склонно к тому, что умение мыслить правильно основывается на жизненном опыте и здравом смысле, а не на базовом знании основ логики и ее приемов.
Конечно, для выполнения простых действий, доведенных до автоматизма, или простых умозаключений хватит и здравого смысла, но чтобы понять или объяснить что-то по-настоящему сложное и важное, одного здравого смысла мало. К тому же он нередко становится причиной неправильных высказываний.
Простые умозаключения в логике
Базой взаимоотношений суждений является общность их содержания. Данная схожесть проявляется в таких логических параметрах:
Поэтому логические взаимоотношения возникают не между всеми высказываниями, а исключительно между теми из них, смысл которых совпадает.
Сравнимыми называются такие простые высказывания, которые содержат одинаковую или смежную терминологию, но различные по качественным или количественным показателям.
Если в двух простых суждениях абсолютно разные субъекты и предикаты, их считают несравнимыми.
Группы простых высказываний
Все простые сравнимые умозаключения можно условно распределить на две подгруппы:
Выделяют три формы совместимости суждений.
Суждения, мысль в которых одинаковая, но преподнесена в разных формах.
«Малыш толкнул стол и разлил молоко»
«Молоко было разлито из-за того, что малыш толкнул стол»
Их характерной особенностью является одновременная истинность при невозможности одновременной ложности.
«Некоторые люди любят гулять»
«Некоторые люди не любят гулять»
Предложения с одним общим предикатом, а субъекты высказываний, выраженные в используемых понятиях, пребывают в логическом подчинении.
«Ни одна просьба ребенка не должна быть невыполненной»
«Некоторые просьбы детей не должны быть невыполненными» (Подчиняющее суждение – первое, а второе выступает в роли подчиненного)
Логический квадрат: история создания
В двадцатом веке В.Ф. Асмус в своей книге «Логика» охарактеризовал понятие «логический квадрат». Суждения и отношения между ними хорошо укладываются в графическую схему квадрата. С его помощью, по мнению ученого, просто и доступно рассмотреть и понять все виды отношений противоположения и подчинения между суждениями.
Г.И. Челпанов определяет метод логического квадрата как схему, наглядно обрисовывающую все возможные виды взаимоотношений между простейшими умозаключениями.
Таким образом, можно дать определение логическому квадрату в логике, как силлогистической диаграмме, которая является мнемонической основой фиксации отношений между категоричными рассуждениями.
Использование логического квадрата для установки отношений между простыми рассуждениями
Выделяют такие виды взаимоотношений для категоричных умозаключений:
Кратко охарактеризовать различные отношения можно в форме таблицы.
Логический квадрат: примеры видов отношений
Между высказываниями, отличающимися и по качественному, и по количественному признаку.
Между А (общим утвердительным высказыванием) и О (частным отрицательным)
Между І (частным утвердительным) и Е (общим отрицательным)
Между суждениями с одинаковым количеством, но разным качеством
Между А (общим утвердительным) и Е (общим отрицательным)
Между разными по качеству частными умозаключениями
Между І (частным утвердительным) и О (частным отрицательным)
В таком отношении состоят высказывания с одним качественным показателем, но разные по количеству, в котором общее становится подчиняющим, а частное подчиненным
Между А (общим утвердительным) и І (частным утвердительным)
Между Е (общим отрицательным) и О (частным отрицательным)
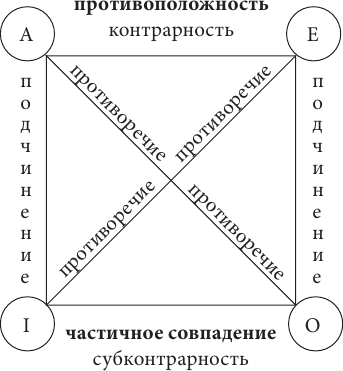
Определить наглядно и запомнить, какие именно отношения по логическому квадрату возможны, поможет его описание. Итак, углы квадрата соотносят с видами умозаключений, а его диагонали и стороны определяют их взаимоотношения.
Истинные зависимости заключений.
Отношения контрадикторности
Остановимся на самом главном вопросе – установлении истинной зависимости умозаключения по логическому квадрату.
Наиболее четко разграниченное и легко определяемое отношение между высказываниями – это отношение противоречия. Оба таких заключения не могут быть правдивыми или ложными одновременно. Правдивость одного исключает правдивость другого. Такие отношения подпадают под действие закона логики про исключение третьего:
Если умозаключение А, являющееся общим утвердительным, правдиво, то противоречащее ему частное отрицательное высказывание О обязательно неправдиво. То же правило проецируется и для отношений между общим отрицательным рассуждением Е и частным утвердительным І.
Отношения контрарности
Если внимательно рассмотреть логический квадрат, виды отношений между высказываниями в нем не всегда однозначны. Примером такой неопределенности служит отношение противоположности. То есть если взять за основу, что общее утвердительное высказывание А истинно, то противоположное ему общее отрицательное Е будет неправдивым. То же правило работает и наоборот.
Но если исходить из того, что исходное суждение А ложно, то умозаключение Е, противоположное ему, может быть как ложным, так и истинным. Все будет зависеть от формального содержания этих высказываний. Исходя из индивидуальной ситуации, можно составить мнение каким по значению – ложным или истинным – будет суждение, противопоставляющееся первому.
Противные умозаключения одновременно правдивыми не бывают, но оба из них могут быть неправдивыми»
Отношения субконтрарности
Отношения частичного совпадения обратно по истинным значениям отношениям противности.
Отношения подпротивоположности не бывают неправдивыми одновременно, хотя бы одно из высказываний обязательно истинно, а бывает и так, что истинны оба.
То есть если взять за первое частное утвердительное высказывание І и предположить, что оно ложно, то в соответствии с логическим квадратом частично совпадающее с ним частное отрицательное высказывание О в обязательном порядке будет правдивым.
Отношения подчинения
Характерной особенностью этих отношений является то, что истинность подчиненного высказывания зависит от истинности подчиняющего. Ложность общих умозаключений никак не соотносится с правдивостью частных, они могут быть как ложными, так и правдивыми в зависимости от ситуации.
Подводя итог, можно сказать, что знание отношений высказываний по логическому квадрату не только позволяет определить их правдивость или неправдивость, но и прийти к правильным выводам во время своих рассуждений или дискуссии с другими людьми.
2.9. Логический квадрат
2.9. Логический квадрат
Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.
Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так если суждение вида А является истинным или ложным, то три других (I, Е, О) сравнимых с ним суждения (т. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники является истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является ложным, и суждение вида О: Некоторые тигры – это не хищники также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.
1. Если суждение вида А является истинным, то суждение вида I также является истинным, а суждения вида Е и О являются ложными.
2. Если суждение вида А является ложным, то суждение вида I является неопределенным по истинности (т. е. может быть как истинным, так и ложным, в зависимости от того, о чем будет идти в нем речь), суждение вида Е является также неопределенным по истинности, а суждение вида О является истинным. (Далее будем применять сокращения, например, вместо выражения «суждение вида А» будем говорить «А», а вместо «является истинным» – просто «истинно»).
3. Если Е истинно, то А ложно, I ложно, О истинно.
4. Если Е ложно, то А неопределенно по истинности, I истинно, О неопределенно по истинности.
5. Если I истинно, то А неопределенно по истинности, Е ложно, О неопределенно по истинности.
6. Если I ложно, то А ложно, Е истинно, О истинно.
7. Если О истинно, то А ложно, Е неопределенно по истинности, I неопределенно по истинности.
8. Если О ложно, то А истинно, Е ложно, I истинно.
Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, – по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также ложно, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
IV. Квадрат коммуникации и генеративная матрица
Исторический и логический методы
Исторический и логический методы По большому счету эмпирический уровень научного познания сам по себе не достаточен для проникновения в сущность вещей, в том числе в закономерности функционирования и развития общества. На определенном этапе, когда накоплено уже более
Логический позитивизм Карнапа
Логический позитивизм Карнапа Логический позитивизм — это видоизмененная форма эмпиризма. Эмпиризм в чистом виде — это учение о том, что все знание мы получаем из чувственного опыта. Логический позитивизм выглядит слабее его в одном важном пункте, но зато сильнее в
Головоломный квадрат
Головоломный квадрат Изображенные на рисунке двадцать кругов образуют крест. Сколько квадратов можно найти в этом кресте, если считать, что любые четыре круга являются углами квадрата? Посмотрите на схему, и вы поймете, что имеется в виду. Четыре круга с буквой А
2. Логический позитивизм
2. Логический позитивизм В 1922 году на кафедре натуральной философии Венского университета, которую после смерти Э. Маха возглавил профессор М. Шлик, собралась группа молодых ученых, поставивших перед собой смелую цель — реформировать науку и философию. Эта группа вошла
Магический квадрат
Магический квадрат Предлагаем наимоднейший способ построить так называемый «магический квадрат». Из колоды игральных карт вытащите десять одной масти — от туза (примем его за единицу) до десятки — и сложите из них квадрат. Причем сложите так, чтобы сумма чисел на
Распили квадрат
Распили квадрат В один прекрасный день Пит Распил ввалился в кафе «Ложки и плошки» и сообщил всем о головоломке, которую только что услыхал от торговца древесиной. Тот показал Питу квадратную деревянную доску с маленьким отверстием в углу. «А теперь, — сказал торговец
2. Логический обвал
2. Логический обвал — То, что может быть продемонстрировано или что требуется доказать, есть конечное познание чего-то особенного. Экзистенция и трансценденция, в смысле этого бытия, не существуют. Если мы мыслим о них, то мысль принимает логические формы, которые
14. Тетрактис и квадрат четырех[119]
14. Тетрактис и квадрат четырех[119] В ходе наших исследований нам уже не раз случалось говорить о пифагорейском Тетрактисе, и мы тогда же привели его числовую формулу: 1+2+3+4=10, указав на связь, непосредственно соединяющую денер с кватернером. Известно совершенно особое
§ 4. Традиционный квадрат противопоставлений
§ 4. Традиционный квадрат противопоставлений Традиционное понимание противопоставления между суждениями отличается от предложенного нами понимания. Поскольку в традиционном подходе все суждения были разложимы на субъект и предикат, противопоставлялись только
ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС?
ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС? Никакого исчерпывающего перечня логических парадоксов не существует. Рассмотренные логические парадоксы – это только часть из всех обнаруженных к настоящему времени. Вполне вероятно, что в будущем будут открыты и многие другие
«Квадрат ресурсов»: ищите узел проблемы
«Квадрат ресурсов»: ищите узел проблемы Если вы затрудняетесь, какие пункты и этапы вам нужно обдумать, имеет смысл воспользоваться стандартной схемой «Четыре блока успеха: Люди, МТБ (материально-техническая база), Деньги и Время». Тут имеется в виду, что для любого
Логический позитивизм
Логический позитивизм В период между первой и второй мировыми войнами были выдвинуты новые философские идеи. Многие из них были стимулированы развитием неклассической физики и стали предметом серьезного эпистемологического анализа со стороны логического позитивизма.
15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb
15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb На этом мы закончим наше краткое сообщение о применении метода бесконечно–малых к логике. Вернее, это не сообщение, а только предложение, только скромный намек на ту область, которая не может не быть огромной. Логика и математика не
Возведение в квадрат и самоусиление
Возведение в квадрат и самоусиление Есть особенно интересный вид умножения, называемый возведением в квадрат, который дает нам подсказки относительно того, как работать с нашими собственными умами. Возведение в квадрат будет очень важно позднее, когда мы будем изучать
Перевоплощение и эксперимент возведения в квадрат
Перевоплощение и эксперимент возведения в квадрат Для начала вспомните недавнее сновидение. Затем выберите из этого сновидения какую-либо фигуру – человека, дерево или что угодно еще.Теперь представьте себе, что эта фигура – основа процесса, начало ее собственной
Логический квадрат (отношения между суждениями)



Сравнимые (идентичные по материалу) суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику являются сравнимыми, так как у них совпадают субъекты и предикаты, а кванторы и связки различаются.
Несравнимые суждения имеют разные субъекты и предикаты. Например, суждения: Все школьники изучают математику, Некоторые спортсмены – это олимпийские чемпионы являются несравнимыми, так как субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыми называются суждения, которые могут быть одновременно истинными. Например, суждения Некоторые люди – это спортсмены, Некоторые люди – это не спортсмены являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в отношениях равнозначности, подчинения или частичного совпадения.
Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения Москва является древним городом, Столица России является древним городом находятся в отношении равнозначности.
Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения Все растения являются живыми организмами, Все цветы (некоторые растения ) являются живыми организмами находятся в отношении подчинения.
Несовместимые суждения могут находиться в отношениях противоположности или противоречия.
Противоположность – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения Все люди являются правдивыми и Все люди не являются правдивыми находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные (Д) и общеотрицательные (Е ).
Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Вернемся к приведенным выше суждениям и убедимся в этом: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми. Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант.
Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями Все люди являются правдивыми и Все люди не являются правдивыми есть третий, средний вариант Некоторые люди являются правдивыми, а некоторые не являются таковыми, который, будучи истинным суждением, обусловливает одновременную ложность двух крайних противоположных суждений.
Противоречие – это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объемами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения Все люди являются правдивыми и Некоторые люди не являются правдивыми находятся в отношении противоречия.
Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот, ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы еще вернемся, когда речь пойдет о логических законах противоречия и исключенного третьего.
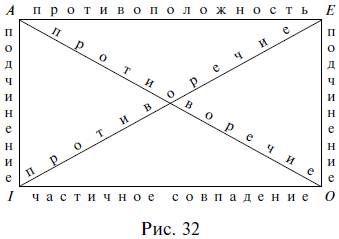
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан еще средневековыми логиками.
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия.
Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О.
Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А ), а второе частноотрицательным (О ), мы без труда устанавливаем отношение между ними с помощью логического квадрата – это противоречие.
Суждения Все люди изучали логику (А ) и Некоторые люди изучали логику (I ) находятся в отношении подчинения, а суждения Все люди изучали логику (А ) и Все люди не изучали логику (Е ) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений (в отличие от понятий) является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так, если суждение вида А является истинным или ложным, то три других (I, Е, О ), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида А ) тоже являются истинными или ложными.
Например, если суждение вида А: Все тигры – это хищники – истинно, то суждение вида I. Некоторые тигры – это хищники – также истинно (если все тигры – хищники, то и часть из них, т. е. некоторые тигры, – это тоже хищники); суждение вида Е Все тигры – это не хищники – ложно, и суждение вида О: Некоторые тигры – это не хищники – также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).