в квадрат вписали равнобедренный треугольник так как это показано на рисунке докажите что одна

Равнобедренный треугольник: свойства, признаки и формулы

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

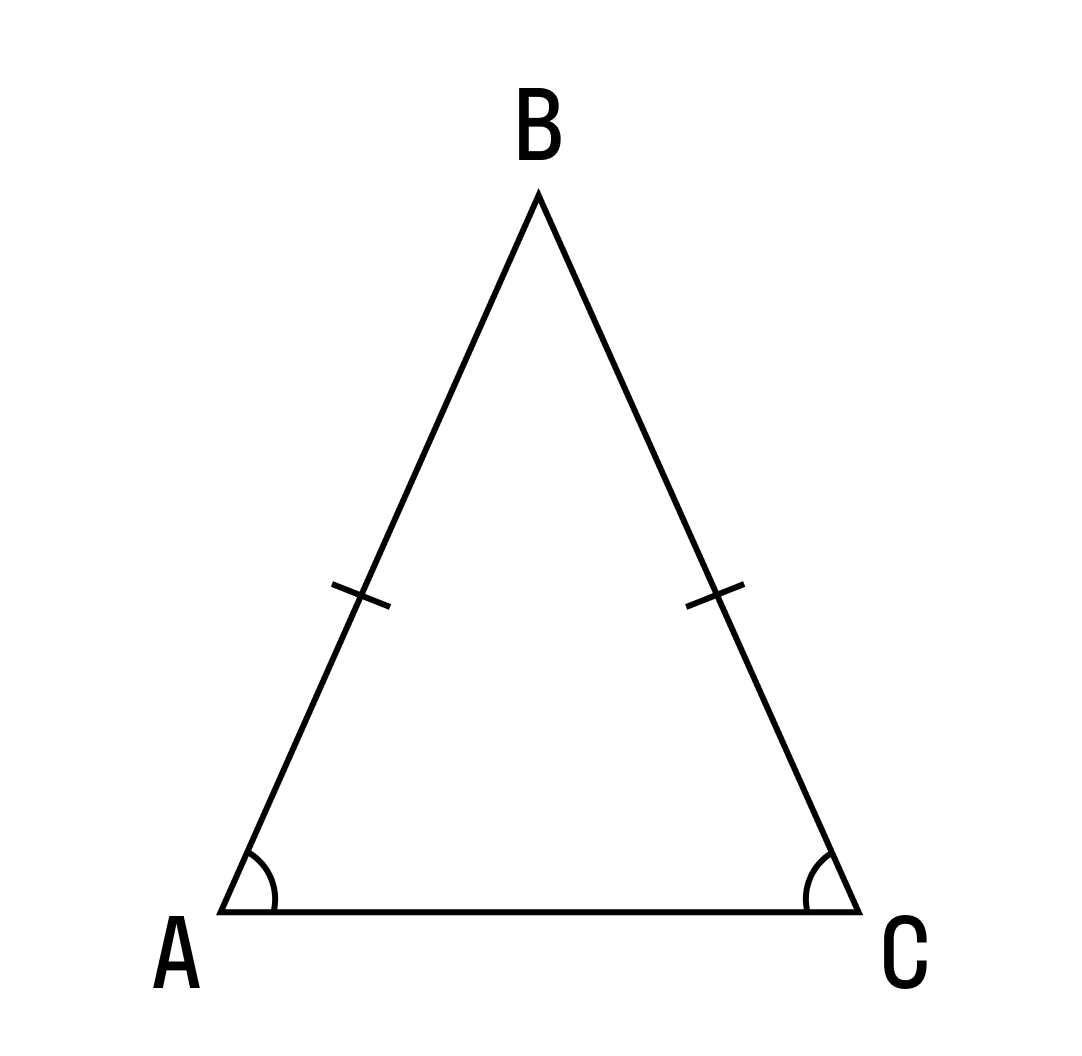
Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.

Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.

А вот и доказательство:

Вуаля, сразу три теоремы доказаны.

Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).

Дано два Δ ABC = Δ A1B1C1.

Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.

Если все стороны совпадают — треугольники равны, а теорема доказана.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

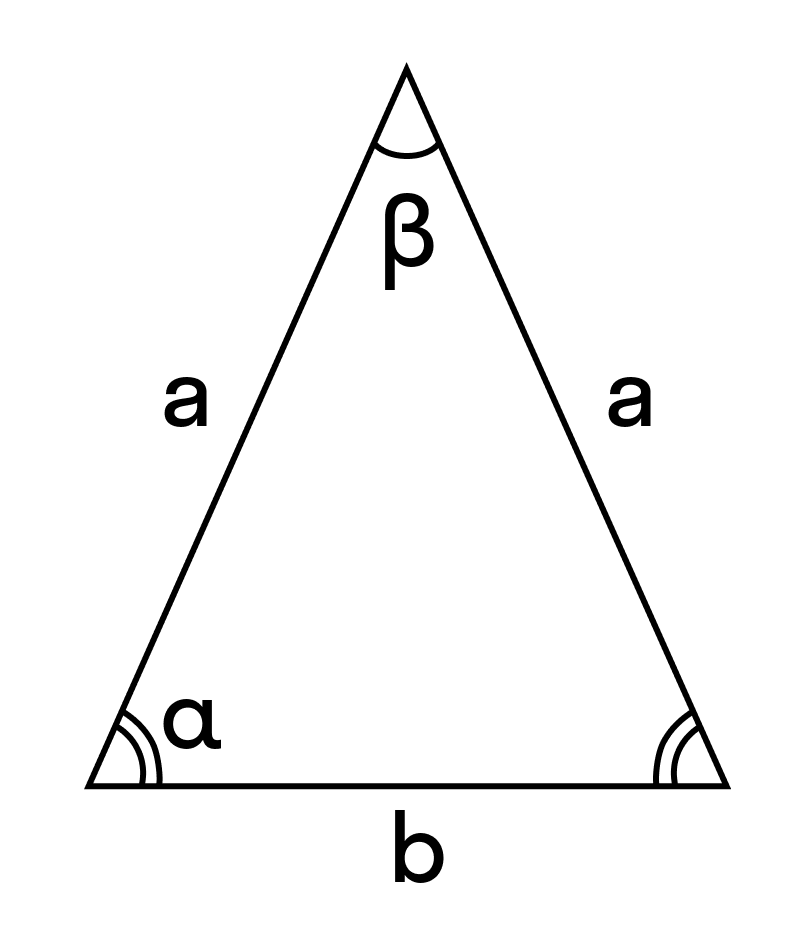
b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

Формулы длины стороны (основания b) равнобедренного треугольника

Формулы длины равных сторон равнобедренного треугольника (стороны a):

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

L — высота, биссектриса и медиана

Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)

Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘

Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.

Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘

Источник

Квадрат вписан равнобедренный треугольник так как это показано на рисунке докажите что одна сторона этого треугольника параллельно диагонали квадрата. ​

Ответы

радиус описаной окружноости = 2*r = 4 см

высота = 3*r = 6 см = а*корень3/2

ответ: ав = вс = 10см, s = 48 кв.см.

1) sполной поверхности = sоснования + sбоковой поверхности

sоснования = a в квадрате. (например а это сторона bc)

формула диагонали квадрата: а в квадрате = а корень из двух, значит сторона а = 6 (см) (т.к. ac=6√2 см) bc = 6 (см)

sосн = а в квадрате = 6*6 = 36(см в кв)

2) sбоковой поыерхности = 1/2*периметр основания*апофему. апофема обозначается буквой l. l это высота sh.

3) роснования = 4а = 4*6 = 24(см)

4) sh является как высотой так и медианой (т.к. треугольник bsc равнобедренный, т.к. пирамида правильная и всё её грани являются равнобедренными треугольниками)

bc = 6 (см), bh = ch = 3 (см)

ob = do = db/2 = 6√2/2 = 3√2 (cм)

5) рассмотрим треугольник obh. он является прямоугольным, т.к. он перпендикулярна к вс (по теореме о перпендикулярности прямой к наклонной в следствии чего прямая перпендикулярна и к проекции)

по теореме пифагора можно найти сторону он.

он = корень из (ов в квадрате минус вн в квадрате)

6) рассмотрим треугольник soh. он прямоугольный(он наклонная и so перпендикуляр). so=5см,он=3см

по теореме пифагора:

sh = корень из (он вквадрате плюс so в квадрате)

sh = корень из (3 в квадрате + 5 в квадрате)

7) sбоковой поверхности = 1/2*периметр основания*апофему

sбоковой поверхности = 1/2*24*корень из 34 = 12*корень из 34 (см в кв)

8) sполной поверхности = sоснования + sбоковой поверхности

sполной поверхности = 36(см в кв) + 12*корень из 34 (см в кв)

3.теорема о вписанном угле: вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°

4.углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.

также равны биссектрисы, медианы и высоты, проведённые из этих углов.

биссектриса, медиана и высота, проведенные к основанию между собой

центры вписанной и описанной окружностей лежат на этой линии

углы, противолежащие равным сторонам, всегда острые (следует из их равенства).

5.квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

6. если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

8. стороны треугольника пропорциональны синусам противолежащих углов

9.в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

11. если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

из второго признака равенства треугольников следует, что: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

13. диагонали ромба пересекаются под прямым углом. диагонали ромба являются биссектрисой его углов

15. серединные перпендикуляры к сторонам треугольника (или другого описываемого окружностью многоугольника) пересекаются в одной точке — центре описанной окружности.

любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Источник