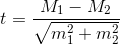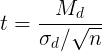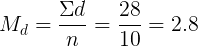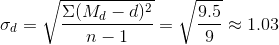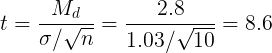Критерий стьюдента для чего используется

Библиотека постов MEDSTATISTIC об анализе медицинских данных

Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic

Критерии и методы

t-КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ НЕЗАВИСИМЫХ СОВОКУПНОСТЕЙ

– общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

Уильям Госсет

1. История разработки t-критерия

Данный критерий был разработан Уильямом Сили Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

2. Для чего используется t-критерий Стьюдента?

t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента

3. В каких случаях можно использовать t-критерий Стьюдента?

Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).

При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.

4. Как рассчитать t-критерий Стьюдента?

Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:

5. Как интерпретировать значение t-критерия Стьюдента?

Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n₁ и n₂). Находим число степеней свободы f по следующей формуле:

После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).

Сравниваем критическое и рассчитанное значения критерия:

6. Пример расчета t-критерия Стьюдента

Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:

Источник

Библиотека постов MEDSTATISTIC об анализе медицинских данных

Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic

Критерии и методы

ПАРНЫЙ t-КРИТЕРИЙ СТЬЮДЕНТА

– одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.

Уильям Госсет

1. История разработки t-критерия

t-критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

2. Для чего используется парный t-критерий Стьюдента?

3. В каких случаях можно использовать парный t-критерий Стьюдента?

Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.

Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.

Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.

4. Как рассчитать парный t-критерий Стьюдента?

Парный t-критерий Стьюдента рассчитывается по следующей формуле:

5. Как интерпретировать значение t-критерия Стьюдента?

Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:

После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p

3. Найдем среднее квадратическое отклонение разностей от средней по формуле:

4. Рассчитаем парный t-критерий Стьюдента:

Источник

6.1 Параметрические критерии

В группу параметрических критериев методов математической статистики входят методы для вычисления описательных статистик, построения графиков на нормальность распределения, проверка гипотез о при­надлежности двух выборок одной совокупности. Эти методы основыва­ются на предположении о том, что распределение выборок подчиняется нормальному (гауссовому) закону распределения. Среди параметрических критериев статистики нами будут рассмотрены критерий Стьюдента и Фишера.

6.1.1 Методы проверки выборки на нормальность

Чтобы определить, имеем ли мы дело с нормальным распределением, можно применять следующие методы:

1) в пределах осей можно нарисовать полигон частоты (эмпирическую функцию распределения) и кривую нормального распределения на основе данных исследования. Исследуя формы кривой нормального распределения и графика эмпирической функции распределения, можно выяснить те параметры, которыми последняя кривая отличается от первой;

2) вычисляется среднее, медиана и мода и на основе этого определяется отклонение от нормального распределения. Если мода, медиана и среднее арифметическое друг от друга значительно не отличаются, мы имеем дело с нормальным распределением. Если медиана значительно отличается от среднего, то мы имеем дело с асимметричной выборкой.

3) эксцесс кривой распределения должен быть равен 0. Кривые с положительным эксцессом значительно вертикальнее кривой нормального распределения. Кривые с отрицательным эксцессом являются более покатистыми по сравнению с кривой нормального распределения;

4) после определения среднего значения распределения частоты и стандартного oтклонения находят следующие четыре интервала распределения сравнивают их с действительными данными ряда:

а) — к интервалу должно относиться около 25% частоты совокупности,

б) — к интервалу должно относиться около 50% частоты совокупности,

в) — к интервалу должно относиться около 75% частоты совокупности,

г) — к интервалу должно относиться около 100% частоты совокупности.

6.1.2 Критерий Стьюдента ( t-критерий)

Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».

При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух неза­висимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.

Статистика критерия для случая несвязанных, независимых выборок равна:

(1)

где , — средние арифметические в эксперименталь­ной и контрольной группах,

— стан­дартная ошибка разности средних арифметических. Находится из формулы:

, (2)

где n ₁ и n ₂ соответственно величины первой и второй выборки.

Если n ₁= n ₂, то стандартная ошибка разности средних арифметических будет считаться по формуле:

(3)

где n величина выборки.

Подсчет числа степеней свободы осуществля­ется по формуле:

Далее необходимо срав­нить полученное значение t _эмп с теоретическим значением t—рас­пределения Стьюдента (см. приложение к учеб­никам статистики). Если t _эмп t _крит, то гипотеза H ₀ принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.

Таблица 1. Результаты эксперимента

Первая группа (экспериментальная) N ₁=11 человек

Вторая группа (контрольная)

12 14 13 16 11 9 13 15 15 18 14

13 9 11 10 7 6 8 10 11

Общее количество членов выборки: n ₁=11, n ₂=9.

Расчет средних арифметических: Х_ср=13,636; Y _ср=9,444

Стандартное отклонение: s _x=2,460; s _y =2,186

По формуле (2) рассчитываем стандартную ошибку разности арифметических средних:

Считаем статистику критерия:

Сравниваем полученное в эксперименте значение t с табличным значением с учетом степеней свободы, равных по формуле (4) числу испытуемых минус два (18).

Табличное значение t_крит равняется 2,1 при допущении возможности риска сделать ошибочное сужде­ние в пяти случаях из ста (уровень значимости=5 % или 0,05).

Если полученное в эксперименте эмпирическое значение t превы­шает табличное, то есть основания принять альтернативную гипотезу (H₁) о том, что учащиеся экспериментальной группы показывают в среднем более высокий уровень знаний. В эксперименте t=3,981, табличное t=2,10, 3,981>2,10, откуда следует вывод о преимуществе эксперимен­тального обучения.

Здесь могут возникнуть такие вопросы:

1. Что если полученное в опыте значение t окажется меньше табличного? Тогда надо принять нулевую гипотезу.

2. Доказано ли преимущество экспериментального метода? Не столько доказано, сколько показано, потому что с самого начала допускается риск ошибиться в пяти случаях из ста (р=0,05). Наш эксперимент мог быть одним из этих пяти случаев. Но 95% возможных случаев говорит в пользу альтернативной гипотезы, а это достаточно убедительный аргумент в статистическом доказательстве.

3. Что если в контрольной группе результаты окажутся выше, чем в экспериментальной? Поменяем, например, местами, сделав средней арифметической эксперимен­тальной группы, a — контрольной:

Отсюда следует вывод, что новый метод пока не про­явил себя с хорошей стороны по разным, возможно, при­чинам. Поскольку абсолютное значение 3,9811>2,1, принимается вторая альтернативная гипотеза (Н₂) о пре­имуществе традиционного метода.

В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле:

(5)

Sd вычисляется по следующей формуле:

(6)

Если t _эмп t _крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Пример 2. Изучался уровень ориентации учащихся на художественно-эстети­ческие ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились бе­седы, выставки детских рисунков, были организованы по­сещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. Закономерно встает вопрос: какова эффективность проведенной работы? С целью проверки эффективности этой работы до начала эксперимента и после давался тест. Из методических со­ображений в таблице 2 приводятся результаты небольшо­го числа испытуемых. [2]

Таблица 2. Результаты эксперимента

до начала экспери­мента (Х)

Вначале произведем расчет по формуле:

Затем применим формулу (6), получим:

И, наконец, следует применить формулу (5). Получим:

Число степеней свободы: k =10-1=9 и по таблице При­ложения 1 находим t_крит =2.262, экспериментальное t=6,678, откуда следует возможность принятия альтерна­тивной гипотезы (H₁) о достоверных различиях средних арифметических, т. е. делается вывод об эффективности экспериментального воздействия.

6.1.3 F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух независимых выборок. Для вычисления F_эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фи­шера такова:

(8)

где — дисперсии первой и второй выборки соответственно.

Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмп всегда будет больше или равно единице.

Чис­ло степеней свободы определяется также просто:

В Приложе­нии 1 критические значения критерия Фишера находятся по величинам k ₁ (верхняя строчка таблицы) и k ₂ (левый столбец таблицы).

Если t _эмп> t _крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. [3] Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.

Решение. Для критерия Фишера необходимо сравнить дис­персии тестовых оценок в обоих классах. Резуль­таты тестирования представлены в таблице:

Рассчитав дисперсии для переменных X и Y, получаем:

Тогда по формуле (8) для расчета по F критерию Фишера находим:

6.2 Непараметрические критерии

Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.

6.2.1 Критерий знаков ( G-критерий)

Критерий предназначен для срав­нения состояния некоторого свойства у членов двух зави­симых выборок на основе измерений, сделанных по шка­ле не ниже ранговой.

Нулевая гипотеза формулируются следующим обра­зом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно раз­личны в одной и той же совокупности при первичном и вторичном измерениях этого свойства.

Ста­тистика критерия (Т) определяется следую­щим образом:

Пример 4. Учащиеся выполняли контрольную ра­боту, направленную на проверку усвоения некоторого понятия. Пятнадцати учащимся затем предложили электронное пособие, составленное с целью фор­мирования данного понятия у учащихся с низким уров­нем обучаемости. После изучения пособия учащиеся снова выполняли ту же контрольного работу, которая оценивалась по пятибалльной системе.

Результаты двукратного выполнения ра­боты представляют измерения по шкале по­рядка (пятибалльная шкала). В этих условиях возмож­но применение знакового критерия для выявления тенденции изменения состояния знаний учащихся после изучения пособия, так как выполняются все допуще­ния этого критерия.

Результаты двукратного выполнения работы (в бал­лах) 15 учащимися запишем в форме таблицы (см. табл. 1). [4]

Источник

Основные статистические критерии. t-критерий Стьюдента

В целях проведения качественного исследования и получения достоверных результатов для дальнейшего анализа и принятия окончательного решения используют различные способы, методы и инструменты. Порой бывает неважно, в какой научной области или отрасли действует автор. Важно лишь грамотно подобрать и использовать необходимые критерии. Одними из таких универсальных параметров являются так называемые статистические критерии, среди которых особое внимание следует уделить t-критерию Стьюдента.

В целях проведения качественного исследования и получения достоверных результатов для дальнейшего анализа и принятия окончательного решения используют различные способы, методы и инструменты. Порой бывает неважно, в какой научной области или отрасли действует автор. Важно лишь грамотно подобрать и использовать необходимые критерии. Одними из таких универсальных параметров являются так называемые статистические критерии, среди которых особое внимание следует уделить t-критерию Стьюдента.

Что это такое?

Этапы проведения исследования

t-критерий Стьюдента – это статистический метод исследования, позволяющий производить сравнение параметров из двух разных выборок, областей. По результатам такого анализа исследователь может делать вывод о сходстве или различии анализируемых объектов. Данный метод успешно используется как в повседневной жизни, так и в различных областях науки (психология, математика, экономика и пр.) и отраслях.

t-критерий Стьюдента чаще всего используется в целях установления взаимосвязи между элементами разных групп. Например, исследователь может анализировать поведение и состояние пациентов с хроническим заболеванием (например, сахарный диабет второго типа) и здоровых людей или имеющих сахарный диабет первого типа и пр.

Нужна помощь преподавателя?

Мы всегда рады Вам помочь!

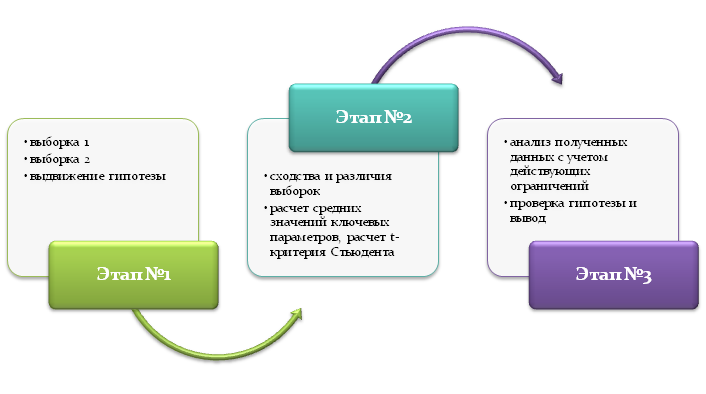
Этапы применения t-критерия Стьюдента

При использовании t-критерия Стьюдента важно, чтобы объекты исследования или анализируемые выборки были распределены равномерно и имели хотя бы минимальное взаимодействие: относились к одной и той же среде, выполняли одно и то же задание и пр. Данное правило называется принципом нормального распределения, когда изучаемые явления/процессы:

t-критерий Стьюдента лучше всего использовать в случаях, когда известны средние значения выборки. Например, эксперт намерен проанализировать средний возраст жителей Сибири и средний возраст россиян по стране. При использовании указанной статистической методики он сможет проверить гипотезу: продолжительность жизни в Сибири дольше, чем в среднем по стране. Для этого достаточно сравнить средние показатели по указанному региону и России. Если отклонений в возрасте не будет, то гипотеза считается верной. Если же будет выявлено некое различие, то важно рассчитать это отклонение.

Схема применения t-критерия Стьюдента выглядит следующим образом:

Чаще всего сравнивают средние показатели конкретного явления, процесса и пр. Для расчета этого критерия можно воспользоваться следующей формулой:

Как используется t-критерий Стьюдента в разных областях науки?

t-критерий Стьюдента – универсальное средство для анализа ситуации, позволяющее установить наличие связей между разными группами элементов. В частности, он успешно применяется в психологии и медицине при проведении различных экспериментов и наблюдений. Исследователи могут сравнивать две группы людей с одним и тем же заболеванием на разных стадиях. Например, первая группа – лица с первичным инсультом, вторая группа – лица со вторичным (неоднократным) инсультом. Гипотеза может быть любой: продолжительность жизни и после первичного инсульта выше чем после вторичного или физическая активность лиц с первичным заболеванием лучше, чем со вторичным и пр.

Применение t-критерия Стьюдента в различных науках

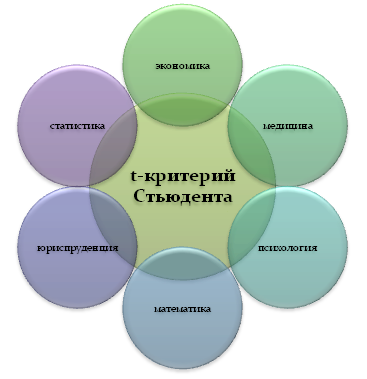
Также t-критерий Стьюдента часто используется в экономике, когда требуется апробировать полученные исследователем результаты. Например, он может сравнивать показатели разных лет, выявлять их динамику и прогнозировать дальнейшее развитие событий (этих же показателей). Здесь автор эксперимента выдвигает гипотезу: анализируемые показатели увеличатся или наоборот уменьшатся.

Ярким примером применения t-критерия Стьюдента является следующая ситуация:

Решение ситуации с помощью t-критерия Стьюдента

Трудности с учебой?

Помощь в написании студенческих и
аспирантских работ!

Источник

t-критерий Стьюдента для проверки гипотезы о средней и расчета доверительного интервала в Excel

Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).

Распределение Стьюдента

Тогда случайная величина

имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.

Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:

Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96s_x̅. Другими словами, являются ли распределения случайных величин

Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.

Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.

Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.

Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:

Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.

Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.

Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.

Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.

Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».

У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина

зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.

Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:

1. средняя X̅ и выборочная дисперсия s 2 являются независимыми величинами;

2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ 2 (хи-квадрат) с таким же количеством степеней свободы, т.е.

где k – количество степеней свободы (на английском degrees of freedom (d.f.))

Вернемся к распределению средней. Разделим числитель и знаменатель выражения

Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.

Тогда исходное выражение примет вид

Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.

Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.

Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин

где ξ распределена по стандартному нормальному закону, а χ 2 _k подчиняется распределению χ 2 c k степенями свободы.

Таким образом, формула критерия Стьюдента для средней арифметической

есть частный случай стьюдентова отношения

Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.

При k > 30 t-критерий практически не отличается от стандартного нормального распределения.

В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.

Условия применения t-критерия Стьюдента

Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.

Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.

Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.

Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.

Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel

В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.

СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.

СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).

СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.

СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.

СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058

СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.

ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.

Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.

Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.

Краткое условие в обще принятых обозначениях выглядит так.

Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.

Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:

Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).

По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.

Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H₀ о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.

Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.

Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.

Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.

Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.

P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.

Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.

Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.

Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.

Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Источник