Корреляционная обработка сигналов что это
Корреляция
Корреляция называют меру схожести двух процессов, в нашем случае — двух сигналов. Такой подход применяется при анализе радиолокационных сигналов во временной области. Он, в частности, полезен для обнаружения периодических сигналов на фоне шума, для установления когерентности между двумя случайными сигналами, а также для определения источников сигналов и времени их излучения.
При обработке радиолокационных сигналов под термином «корреляция» понимают сравнение неизвестного сигнала (сигнала с неизвестными параметрами) с известным эталонным сигналом для определения степени их схожести в зависимости от рассогласования (смещения) одного относительно другого. Получаемая функция имеет аргументом относительное расстояние между сигналами на оси времени, а ее математическое выражение имеет различный вид для случаев аналоговой и цифровой обработки сигналов.
Для аналоговых сигналов эта функция представляет собой непрерывную сумму (интеграл) произведений совпадающих (перекрывающих друг друга) частей двух сигналов:
Для дискретных или цифровых сигналов — это сумма произведений совпадающих (перекрывающих друг друга) субимпульсов:
Эталонный сигнал, как правило, нормирован или представляет собой идеализированную модель. Численные значения корреляции (коэффициент корреляции) на выходе вычислительного устройства будут не полностью нормированы, поскольку максимальная корреляция будет меньше 1. Только в случае, когда неизвестный сигнал идентичен эталонному, значение корреляции будет равным 1. Такой важный частный случай называют автокорреляцией. Автокорреляцию используют в поиске периодичностей.
Примеры практического применения корреляционной обработки — согласованный фильтр, измерение дальности в шумовом радиолокаторе.
Что такое корреляционная обработка сигнала и как она работает
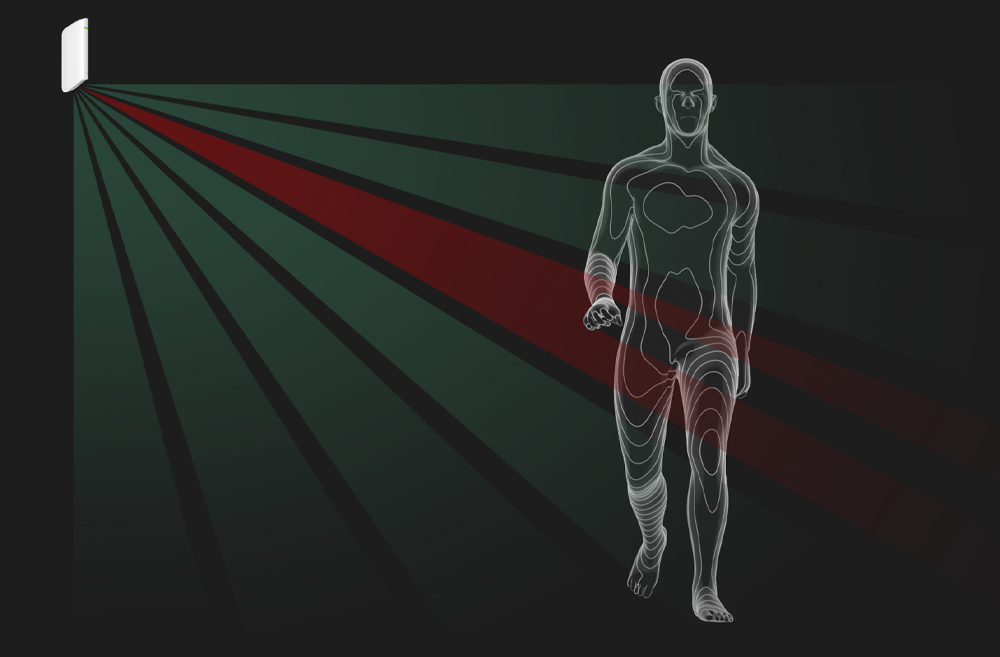
Корреляционная обработка сигнала — это метод защиты от ложных срабатываний, который используется в датчиках движения типа “штора” MotionProtect Curtain.
Датчики движения на основе PIR-сенсоров улавливают инфракрасное излучение, иначе говоря, тепло.
Иногда говорят: «Датчик движения увидел человека». На самом деле эти устройства не видят предметов, животных или людей, они только обрабатывают данные.
Оптическая система датчика фокусирует инфракрасное излучение на PIR-сенсор датчика. Затем сигналы сенсора направляются в микропроцессор, где преобразовываются в числовые данные. А дальше происходит анализ и оценка. Зная интенсивность инфракрасного излучения и динамику перемещения источника, программные алгоритмы определяют характер угрозы, и датчик принимает решение: проигнорировать сигнал или поднять тревогу.
Как работает корреляционная обработка сигнала
Корреляционная обработка сигнала опциональна и активируется в настройках датчика. Когда опция активна, MotionProtect Curtain анализирует сигналы с двух PIR-сенсоров в три этапа:
Оранжевый — зоны видимости первого PIR-сенсора, зелёный — зоны видимости второго PIR-сенсора
Как работает датчик, если корреляционная обработка сигнала отключена
Когда опция корреляционной обработки сигнала не активна, MotionProtect Curtain передает тревогу хабу при регистрации характерного для движения инфракрасного излучения даже одним из PIR-сенсоров.
Когда рекомендуется использовать корреляционную обработку сигнала
Корреляционную обработку сигнала стоит включить в таких ситуациях:
Учитывайте, что при включенной корреляционной обработке сигналов уменьшается дальность обнаружения движения. Итоговая дальность зависит от чувствительности датчика:
Корреляция (обработка сигналов)
Содержание
Обработка сигналов
Обработка изображения
Одним из применений корреляции изображений является, например, распознавание определенных объектов или структур. Структуры могут быть: узор объемного материала (размер или форма), проверенный узор скатерти, раковые клетки, функциональные или нефункциональные клетки крови. Это приложение очень интересно, если задача состоит в том, чтобы распознать или отсортировать объекты (хорошие или плохие или расположение по размеру). Пример: определение подлинности банкноты или подделки.
Кроме того, сами изображения могут быть изменены с помощью корреляции путем фильтрации определенных структур (гармоник). Пример: удаление элементов изображения с экрана телевизора для получения гладкого изображения. Чтобы удалить информацию об изображении из маски экрана, все частотные компоненты, составляющие пиксели, отфильтровываются. Остается изображение без пикселей. Последующий анализ дает информацию о том, какие частотные компоненты отсутствуют.
Количественное описание
Здесь должны быть описаны соединения с точки зрения обработки сигналов и анализа сигналов с непрерывными сигналами.
Корреляционный интеграл
Математически корреляция описывается корреляционным интегралом для функций времени:
Следующее относится к сложным функциям времени:
Значение K и пределы интеграла должны быть адаптированы к соответствующим функциям:
Функция шаблона m ( t )
m (t) может быть любой функцией шаблона. Однако его следует разумно адаптировать.
Коэффициент корреляции как мера подобия двух сигналов
Энергия сигнала E s действительного сигнала s вычисляется следующим образом
Полезно рассчитать энергию пересечения с энергиями сигнала с помощью уравнения
Как видно из примеров, коэффициент корреляции является мерой того, насколько похожи два сигнала.
Здесь коэффициент перекрестной мощности определяет степень соответствия двух сигналов. Для одного называет оба сигнала ортогональными. Чем он больше, тем больше вероятность того, что оба сигнала как-то связаны друг с другом. ρ ¯ знак равно п Икс y п Икс п y <\ Displaystyle <\ overline <\ rho>> = <\ tfrac 

Автокорреляционная функция
Он рассчитывается для сигнала мощности с действительным знаком.
В случае энергетических сигналов результат аналогичен
Для комплексных сигналов следующие результаты:
Приложения
Применение в обработке изображений
На фотографиях в последовательности слева изображена молодая женщина, ее негативный образ, Ницше и случайный рисунок шума.
Чтобы проверить, можно ли найти фотографию молодой женщины в зашумленных изображениях, все четыре изображения были сначала наложены с белым гауссовым шумом, а затем коррелированы с ее фотографией (первая фотография в последовательности изображений).
Картина корреляции Ницше мало согласуется с картиной молодой женщины, диаграмма шума почти отсутствует. Хорошо видна положительная и отрицательная корреляция с изображениями женщины и ее отрицательными.
В более широком смысле так называемые оптические компьютеры (оптика Фурье, 4f) основаны на корреляции. Системы, также известные как корреляторы Фурье, коррелируют изображения с помощью голограмм. С оптикой 4f корреляция в частотной области может быть достигнута с помощью чисто физического процесса почти со скоростью света. Требуется оптическая скамья с соответствующей системой линз и линзами Фурье.
Применение в обработке глины
В стереофонии корреляция описывает подобие сигналов. Нормализованный коэффициент корреляции или коэффициент корреляции является мерой подобия двух сигналов и вычисляется упрощенным способом из наибольшего возможного интеграла по времени разности амплитуд между этими двумя сигналами. Это приблизительно указывается измерителями степени корреляции, хотя на практике они проверяют только эталон фазы с очень коротким временем интегрирования, составляющим менее одной секунды.
Применение в многоканальной передаче сигнала
Применение при приеме сигнала
КОРРЕЛЯЦИЯ СИГНАЛОВ
Предельный страх и предельный пыл храбрости одинаково расстраивают желудок и вызывают понос.
Мишель Монтень. Французский юрист-мыслитель, XVI в.
Вот это номер! Две функции имеют стопроцентную корреляцию с третьей и ортогональны друг другу. Ну и шуточки были у Всевышнего при сотворении Мира.
Анатолий Пышминцев. Новосибирский геофизик Уральской школы, ХХ в.
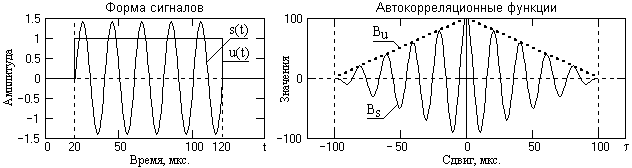
8.2. Взаимнокорреляционные функции сигналов (ВКФ).
Корреляция (correlation), и ее частный случай для центрированных сигналов – ковариация, является методом анализа сигналов. Приведем один из вариантов использования метода. Допустим, что имеется сигнал s(t), в котором может быть (а может и не быть) некоторая последовательность x(t) конечной длины Т, временное положение которой нас интересует. Для поиска этой последовательности в скользящем по сигналу s(t) временном окне длиной Т вычисляются скалярные произведения сигналов s(t) и x(t). Тем самым мы «прикладываем» искомый сигнал x(t) к сигналу s(t), скользя по его аргументу, и по величине скалярного произведения оцениваем степень сходства сигналов в точках сравнения.
Корреляционный анализ дает возможность установить в сигналах (или в рядах цифровых данных сигналов) наличие определенной связи изменения значений сигналов по независимой переменной, то есть, когда большие значения одного сигнала (относительно средних значений сигнала) связаны с большими значениями другого сигнала (положительная корреляция), или, наоборот, малые значения одного сигнала связаны с большими значениями другого (отрицательная корреляция), или данные двух сигналов никак не связаны (нулевая корреляция).
В варианте автокорреляции (autocorrelation) по аналогичной методике производится определение скалярного произведения сигнала s(t) с собственной копией, скользящей по аргументу. Автокорреляция позволяет оценить среднестатистическую зависимость текущих отсчетов сигнала от своих предыдущих и последующих значений (так называемый радиус корреляции значений сигнала), а также выявить в сигнале наличие периодически повторяющихся элементов.
Особое значение методы корреляции имеют при анализе случайных процессов для выявления неслучайных составляющих и оценки неслучайных параметров этих процессов.
Заметим, что в терминах «корреляция» и «ковариация» в настоящее время существует изрядная путаница. В иностранной литературе термин «ковариация» применяется к центрированным функциям, а «корреляция» – к произвольным. В отечественной литературе, и особенно в литературе по сигналам и их обработке, довольно часто применяется прямо противоположная терминология. Однако при переводах иностранной литературы терминология, как правило, не изменяется, и начинает все шире проникать в отечественную литературу. Принципиального значения это не имеет, но при знакомстве с литературными источниками стоит обращать внимание на принятое назначение данных терминов.
При разработке настоящих лекций было принято решение использовать общепринятую международную терминологию, как согласованную по понятиям с основными положениями теории вероятностей и математической статистики.
8.1. Автокорреляционные функции сигналов [1,25].
Понятие автокорреляционных функций (АКФ) сигналов. АКФ (correlation function, CF) сигнала s(t), конечного по энергии, является количественной интегральной характеристикой формы сигнала, и определяется интегралом от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время t :
B s ( t ) =
АКФ относится к четным функциям, в чем нетрудно убедиться заменой переменной t = t- t в выражении (8.1.1):
B s ( t ) = 

Максимум АКФ, равный энергии сигнала при t =0, всегда положителен, а модуль АКФ при любом значении временного сдвига не превосходит энергии сигнала. Последнее прямо вытекает из свойств скалярного произведения (как и неравенство Коши-Буняковского):
б s(t), s(t+ t ) с = ||s(t)|| Ч ||s(t+ t) || Ч cos j ( t ),
B s ( t ) = 
По мере увеличения значения величины сдвига t для финитных сигналов временное перекрытие сигнала с его копией уменьшается, а, соответственно, косинус угла взаимодействия и скалярное произведение в целом стремятся к нулю:
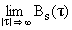
АКФ, вычисленная по центрированному значению сигнала s(t), представляет собой автоковариационную функцию сигнала:
C s ( t ) =
где m s – среднее значение сигнала. Ковариационные функции связаны с корреляционным функциями достаточно простым соотношением:
B s ( t ) =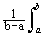
АКФ может быть вычислена и для слабозатухающих сигналов с бесконечной энергией, как среднее значение скалярного произведения сигнала и его копии при устремлении интервала задания сигнала к бесконечности:
B s ( t ) = 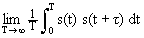
АКФ по данным выражениям имеет физическую размерность мощности, и равна средней взаимной мощности сигнала и его копии в функциональной зависимости от сдвига копии.
Иногда эту функцию называют «истинной» автокорреляционной функцией. В силу нормировки ее значения не зависят от единиц (масштаба) представления значений сигнала s(t) и характеризуют степень линейной связи между значениями сигнала в зависимости от величины сдвига t между отсчетами сигнала. Так, например, для шумовых сигналов при полной статистической независимости отсчетов по независимой переменной, значение r s ( t ) стремится к нулю при t ≠ 0, и стремится к 1 при t ® 0.
АКФ периодических сигналов. Энергия периодических сигналов бесконечна, поэтому АКФ периодических сигналов вычисляется по одному периоду Т, с усреднением скалярного произведения сигнала и его сдвинутой копии в пределах этого периода:
B s ( t ) = (1/Т) 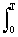
Математически более строгое выражение:
B s ( t ) = 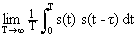
При t =0 значение нормированной на период АКФ равно средней мощности сигналов в пределах периода. При этом АКФ периодических сигналов является периодической функцией с тем же периодом Т. Так, для сигнала s(t) = A cos( w 0 t+ j 0 ) при T=2 p / w 0 имеем:
B s ( t ) = 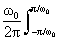
Полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств АКФ. С помощью функций автокорреляции можно проверять наличие периодических свойств в любых произвольных сигналах.
АКФ дискретных сигналов. При интервале дискретизации данных D t = const вычисление АКФ выполняется по интервалам Dt = D t и обычно записывается, как дискретная функция номеров n сдвига отсчетов n Dt :
Дискретные сигналы обычно задаются в виде числовых массивов определенной длины с нумерацией отсчетов к = 0,1,…N, а вычисление дискретной АКФ выполняется в одностороннем варианте с учетом длины массивов по формуле:
Множитель N/(N+1-n) в данной функции является поправочным коэффициентом на постепенное уменьшение числа перемножаемых и суммируемых значений (от N до N-n) по мере увеличения сдвига n. Без этой поправки для нецентрированных сигналов в значениях АКФ появляется тренд суммирования средних значений.
Практически, дискретная АКФ имеет такие же свойства, как и непрерывная АКФ. Она также является четной, а ее значение при n = 0 равно мощности дискретного сигнала.
Кодовые сигналы являются разновидностью дискретных сигналов. На определенном интервале кодового слова М Ч D t они могут иметь только два амплитудных значения: 0 и 1 или 1 и –1. При выделении кодов на существенном уровне шумов форма АКФ кодового слова имеет особое значение. С этой позиции наилучшими считаются такие коды, значения боковых лепестков АКФ которых минимальны по всей длине интервала кодового слова при максимальном значении центрального пика. К числу таких кодов относится код Баркера, приведенный в таблице 8.1. Как видно из таблицы, амплитуда центрального пика кода численно равна значению М, при этом амплитуда боковых осцилляций при n № 0 не превышает 1.
Курс лекций «Основы цифровой обработки сигналов»
Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.
Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.
Список лекций
Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в Центре Современной Электроники, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.
Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.
Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:
Список лекций — достаточный но, разумеется, неполный для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.
Где найти?
Все материалы — абсолютно бесплатны и доступны в виде открытого репозитория на моем гитхабе как opensource проект. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).
Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!
Сигналы. Z-преобразование
Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).
Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.
Такая трактовка справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты. Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.
Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.
Пример конечной дискретной последовательности:
.
Пример этой же последовательности в Z-форме:
Преобразование Фурье. Свойства. ДПФ и БПФ
В этом разделе описывается понятие временной и частотной области сигнала. Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.
В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).
Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.
Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.
Спектр гармонического сигнала:
Сравнение эффективности ДПФ и БПФ
Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:
| N | ДПФ | БПФ | Отношение числа комплексных сложений | Отношение числа комплексных умножений | ||
|---|---|---|---|---|---|---|
| Число операций умножения | Число операций сложения | Число операций умножения | Число операций сложения | |||
| 2 | 4 | 2 | 1 | 2 | 4 | 1 |
| 4 | 16 | 12 | 4 | 8 | 4 | 1.5 |
| 8 | 64 | 56 | 12 | 24 | 5.3 | 2.3 |
| 16 | 256 | 240 | 32 | 64 | 8 | 3.75 |
| 32 | 1024 | 992 | 80 | 160 | 12.8 | 6.2 |
| 64 | 4096 | 4032 | 192 | 384 | 21.3 | 10.5 |
| 128 | 16384 | 16256 | 448 | 896 | 36.6 | 18.1 |
| . | . | . | . | . | . | . |
| 4096 | 16777216 | 16773120 | 24576 | 49152 | 683 | 341 |
| 8192 | 67108864 | 67100672 | 53248 | 106496 | 1260 | 630 |
Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!
Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.
Свертка и корреляция
В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.
В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.
Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.
Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).
В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).
Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.
| N | Свертка | Быстрая свертка | Отношение |
|---|---|---|---|
| 8 | 64 | 448 | 0.14 |
| 16 | 256 | 1088 | 0.24 |
| 32 | 1024 | 2560 | 0.4 |
| 64 | 4096 | 5888 | 0.7 |
| 128 | 16K | 13312 | 1.23 |
| . | . | .. | . |
| 2048 | 4M | 311296 | 13.5 |
Случайные сигналы и шум
В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (или корень этой величины — среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие белого шума, как основного источника шумов (помех) при обработке сигналов.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:
В задачах ЦОС случайные сигналы делятся на два класса:
С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).
Сигналы, модуляция и манипуляция
В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.
Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:
Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).
Цифровые фильтры — БИХ и КИХ
Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются фильтрами. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.
В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.
Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.
Оконные функции в задачах фильтрации
Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.
Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).
Ресемплинг. Децимация и интерполяция
В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.
Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.
Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.
График АЧХ фильтра в зависимости от коэффициента децимации:
Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.
Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.
Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.
Заключение
Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!
Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).