Корень что это математика
Арифметический корень.
Длина стороны квадрата не может быть отрицательным числом, поэтому искомая стороны квадрата 3 см.
Корнем n -й степени из числа α является такое число b, где b n = α.
Здесь n—натуральное число принято называть показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай n = 1 банально.
Мы получили положительное и отрицательное значение корня. Эта особенность усложняет расчеты. Чтобы добиться однозначность, было введено понятие арифметического корня, значение которого всегда со знаком плюс, то есть только положительное.
Корень называется арифметическим, если он извлекается из положительного числа и сам является положительным числом.
Арифметический корень заданной степени из заданного числа существует только один.
Операцию расчетов принято называть «извлечением корня n-й степени» из числа α. По сути мы выполняем операцию обратную к возведению в степень, а именно — нахождение основания степени b по известному показателю n и результату возведения в степень
Корни второй и третьей степени используются на практике чаще остальных и поэтому им были даны специальные названия.
Квадратный корень: В этом случае показатель степени 2 принято не писать, а термин «корень» без указания степени чаще всего означает квадратный корень. Геометрически толкование, является длина стороны квадрата, площадь которого равна α.
Кубический корень: Геометрически толкованием, выступает длина ребра куба, объём которого равен α.
Свойства арифметических корней.
1) При вычислении арифметического корня из произведения, необходимо извлечь его из каждого сомножителя отдельно
2) Для расчета корня из дроби, необходимо извлечь его из числителя и знаменателя данной дроби
3) При расчете корня из степени, необходимо разделить показатель степени на показатель корня
Первые расчеты, связанные с извлечением квадратного корня, обнаружены в работах математиков древнего Вавилона и Китая, Индии, Греции (о достижениях древнего Египта в этом отношении в источниках информация отсутствует).
Математики древнего Вавилона (II тысячелетие до н. э.) применяли для извлечения квадратного корня особый численный метод. Начальное приближение для квадратного корня находили исходя из ближайшего к корню (в меньшую сторону) натурального числа n. Представив подкоренное выражение в виде: α=n 2 +r, получаем: x0=n+r/2n, затем применялся итеративный процесс уточнения:
Итерации в этом методе очень быстро сходятся. Для ,
Например, α=5; n=2; r=1; x0=9/4=2,25 и мы получаем последовательность приближений:
В заключительном значении верны все цифры, кроме последней.
Греки сформулировали проблему удвоения куба, которая сводилась к построению кубического корня с помощью циркуля и линейки. Правила вычисления любой степени из целого числа, изучены математиками Индии и арабских государств. Далее они получили широкое развитие в средневековой Европе.
Сегодня для удобства расчетов квадратных и кубических корней широко используются калькуляторы.
Корень что это математика
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )
Сам значок называется красивым словом «радикал«.
Как извлечь корень? Это лучше рассмотреть на примерах.
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры:


Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но. Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек. Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень.
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах.
Пунктик первый. Корни надо узнавать в лицо!
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.
Попробуем вычислить вот такой корень:
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Квадратные корни из отрицательных чисел извлечь нельзя!
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить. Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками



и так далее, скрываются просто числа! Неровные, лохматые, иррациональные, но числа!
Конечно, если корень из числа извлекается ровно, вы обязаны это сделать. Ответ задания в виде, например
никто не оценит. Надо корень посчитать и написать
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах. Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Верно. Два. Но ведь и минус два даст в квадрате 4. А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит. Это тоже корень квадратный из четырёх.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
Но если вы решаете какое-нибудь квадратное уравнение, типа:
то всегда получается два ответа (с плюсом и минусом):
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор. извините, камни!)
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
А вот здесь можно познакомиться с функциями и производными.
Свойства корней.
Свойства квадратных корней.
Обратно, чтобы извлечь корень из степени, достаточно возвести в эту степень корень из основания степени:
Обратно, произведение корней одной и той же степени равно корню той же степени из произведения подкоренных значений:
Квадратный корень как элементарная функция.
Квадратный корень – это элементарная функция и частный случай степенной функции 


Как функция комплексный переменный корень — двузначная функция, у которой листы сходятся в нуле.
Свойство корня как функции.
На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.
То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:
Теперь определим свойства функции корня и построим ее график.
Основные свойства корня как функции:
Промежуток [0; +∞) – является областью определения.
Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.
Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.
Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.
Значит можно утверждать, что:
Теперь можно построить график функции корня.
Пользуясь графиком, можно записать оставшиеся свойства функции.
На промежутке [0; +∞) функция возрастает.
На всей области определения функция выпукла вверх.
У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.
Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.
В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0.
Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.
Извлечение корней: методы, способы, решения
Из этой статьи вы узнаете:
Что такое «извлечение корня»
Для начала введем определение «извлечение корня».
Извлечение корня — процесс нахождения значения корня.
Выражения «извлечение корня» и «нахождение значения корня» равнозначны.
В каких случаях извлекается корень?
Принципы нахождения значения корня и способы их извлечения
Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.
Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.
Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).
Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.
Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.
И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.
Использование таблицы квадратов, кубов и т.д.
Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.
Таблица квадратов
| Таблица квадратов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2041 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.
Таблица кубов
| Таблица кубов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 | |
| 2 | 8000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 | |
| 3 | 27000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 | |
| 4 | 64000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 | |
| 5 | 125000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 | |
| 6 | 216000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 | |
| 7 | 343000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 | |
| 8 | 512000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 | |
| 729000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 | ||
Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.
Разложение подкоренного числа на простые множители
Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.
Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.
Разложим 144 на простые множители:
Также при использовании свойств степени и корней можно записать преобразование немного по-другому:
144 = 2 × 2 × 2 × 2 × 3 × 3 = 2 4 × 3 2 = 2 4 × 3 2 = 2 2 × 3 = 12
Извлечение корней из дробных чисел
Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.
Следуя свойству корня из частного, справедливым является следующее равенство:
Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.
Извлечение корня из отрицательных чисел
Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.
Затем следует заменить смешанное число обыкновенной дробью:
Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:
Вычисляем корни в числителе и знаменателе:
Краткая запись решения:
Поразрядное нахождение значения корня
В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.
| Возможное значение корня | 2,0 | 2,1 | 2,2 | 2,3 |
| Это значение в степени | 4 | 4,41 | 4,84 | 5,29 |
| Возможное значение корня | 2.20 | 2,21 | 2,22 | 2,23 | 2,24 |
| Это значение в степени | 4,84 | 4,8841 | 4,8294 | 4,9729 | 5,0176 |
Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.
Вычислить квадратный корень из числа

Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
| Число знаков после запятой: |
| √ |
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
25, 36, 49 — квадратные числа, поскольку:
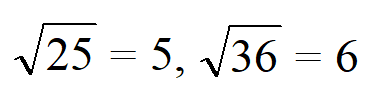
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 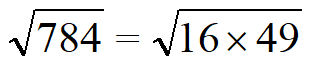 |
| Применим правило Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. | 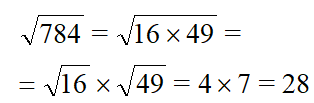 Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 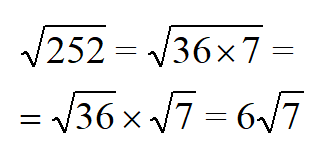 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76 7. |
| Вычисляем корень | 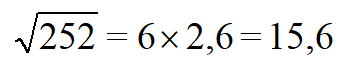 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. | 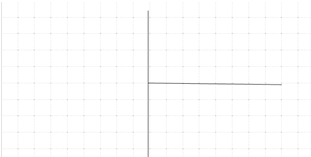 |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так: — целую часть справа налево; — число после запятой слева направо. | Пример: 3459842,825694 → 3 45 98 42, 82 56 94 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = | 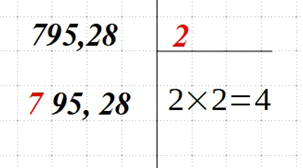 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. | 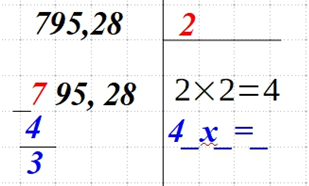 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 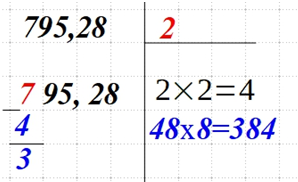 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева. | 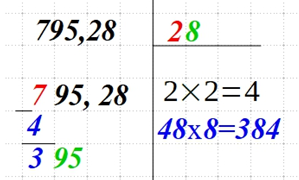 |
| Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. | 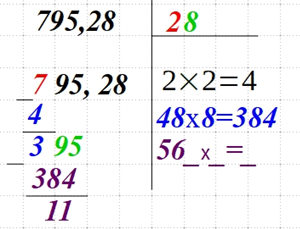 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. | 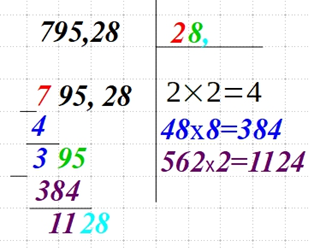 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 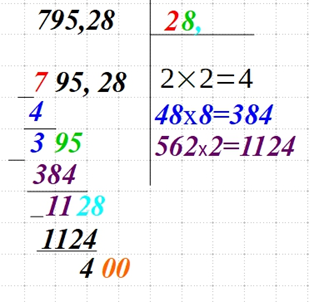 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.































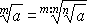
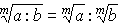

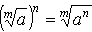
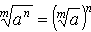
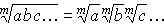







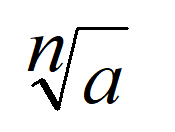
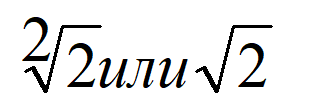
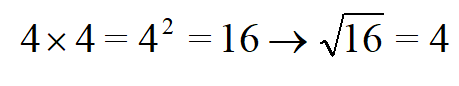
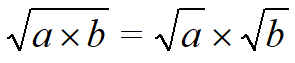
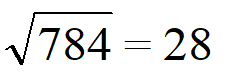
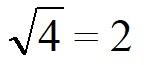
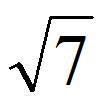 между 2 и 4.
между 2 и 4.