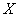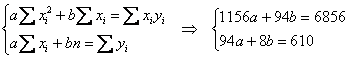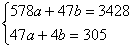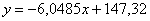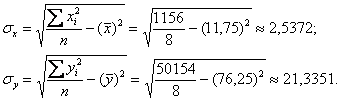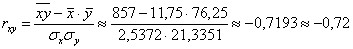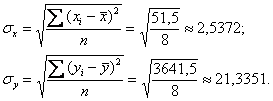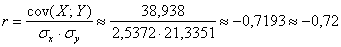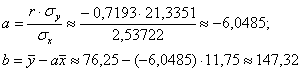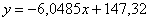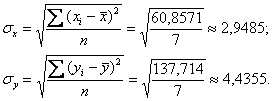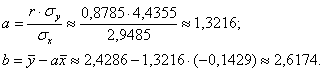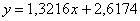Коэффициент корреляции характеризует что
Корреляция и коэффициент корреляции
Корреляция — степень связи между 2-мя или несколькими независимыми явлениями.
Корреляция бывает положительной и отрицательной.
Положительная корреляция (прямая) возникает при одновременном изменении 2-х переменных величин в одинаковых направлениях (в положительном или отрицательном). Например, взаимосвязь между количеством пользователей, приходящих на сайт из поисковой выдачи и нагрузкой на сервер: чем больше пользователей, тем больше нагрузка.
Корреляция отрицательна (обратная), если изменение одной величины приводит противоположному изменению другой. Например, с увеличением налоговой нагрузки на компании уменьшается их прибыль. Чем больше налогов, тем меньше денег на развитие.

Эффективность корреляции как статистического инструмента заключается в возможности выражения связи между двумя переменными при помощи коэффициента корреляции.
При значении КК равным 1, следует понимать, что при каждом изменении 1-й переменной происходит эквивалентное изменение 2-й переменной в том же направлении.


| Значение | Интерпретация |
| до 0,2 | Очень слабая |
| до 0,5 | Слабая |
| до 0,7 | Средняя |
| до 0,9 | Высокая |
| свыше 0,9 | Очень высокая корреляция |
Данный метод обработки статистической информации популярен в экономических, технических, социальных и других науках в виду простоты подсчета КК, простотой интерпретации результатов и отсутствия необходимости владения математикой на высоком уровне.
Корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях: положительная или отрицательная корреляция между 2-мя переменными не обязательно означает, что изменение одной переменной вызывает изменение другой.
Например, есть положительная корреляция между увеличением зарплаты менеджеров по продажам и качеством работы с клиентами (повышения качества обслуживания, работа с возражениями, знание положительных качеств продукта в сравнении с конкурентами) при соответствующей мотивации персонала. Увеличившийся объем продаж, а следовательно и зарплата менеджеров, вовсе не означает что менеджеры улучшили качество работы с клиентами. Вполне вероятно, что случайно поступили крупные заказы и были отгружены или отдел маркетинга увеличил рекламный бюджет или произошло еще что-то.
Возможно существует некая третья переменная, влияющая на причину наличия или отсутствия корреляции.
Коэффициент корреляции не рассчитывается:
Коэффициент корреляции
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Содержание
Коэффициент корреляции
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
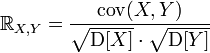
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
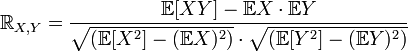
где символ 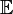
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов ( корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.
Ограничения корреляционного анализа
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
Полезное
Смотреть что такое «Коэффициент корреляции» в других словарях:
Коэффициент корреляции — Математическое представление о степени связи между двумя сериями измерений. Коэффициент +1 обозначает четкую позитивную корреляцию: высокие показатели по одному параметру (например, рост) точно соотносятся с высокими показателями по другому… … Большая психологическая энциклопедия
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ — англ. coefficient, correlation; нем. Korrelationskoeffizient. Мера тесноты связи двух или более переменных. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
коэффициент корреляции — — [http://www.dunwoodypress.com/148/PDF/Biotech Eng Rus.pdf] Тематики биотехнологии EN correlation coefficient … Справочник технического переводчика
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
коэффициент корреляции — 1.33. коэффициент корреляции Отношение ковариации двух случайных величин к произведению их стандартных отклонений: Примечания 1. Эта величина всегда будет принимать значения от минус 1 до плюс 1, включая крайние значения. 2. Если две случайные… … Словарь-справочник терминов нормативно-технической документации
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ — (correlation coefficient) мера ассоциации одной переменной с другой. См. Корреляция; Коэффициент корреляции производного значения Пирсона; Коэффициент ранговой корреляции спирмена … Большой толковый социологический словарь
Коэффициент корреляции — CORRELATION COEFFICIENT Показатель степени линейной зависимости между двумя переменными величинами: Коэффициент корреляции может изменяться в пределах от 1 до 1. Если большим значениям одной величины соответствуют большие значения другой (и… … Словарь-справочник по экономике
коэффициент корреляции — koreliacijos koeficientas statusas T sritis automatika atitikmenys: angl. correlation coefficient vok. Korrelationskoeffizient, m rus. коэффициент корреляции, m pranc. coefficient de corrélation, m … Automatikos terminų žodynas
коэффициент корреляции — koreliacijos koeficientas statusas T sritis fizika atitikmenys: angl. correlation coefficient vok. Korrelationskoeffizient, m rus. коэффициент корреляции, m pranc. coefficient de corrélation, m … Fizikos terminų žodynas
Корреляция, корреляционная зависимость
Корреляция (от лат. correlatio), корреляционная зависимость — взаимозависимость двух или нескольких случайных величин. Суть ее заключается в том, что при изменении значения одной переменной происходит закономерное изменение (уменьшению или увеличению) другой(-их) переменной(-ых).
При расчете корреляций пытаются определить, существует ли статистически достоверная связь между двумя или несколькими переменными в одной или нескольких выборках. Например, взаимосвязь между ростом и весом детей, взаимосвязь между успеваемостью и результатами выполнения теста IQ, между стажем работы и производительностью труда.
Важно понимать, что корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях. Например, если бы исследуемой выборке между ростом и весом человека существовала корреляционная зависимость то, это не значило бы, что вес является причиной роста человека, иначе сбрасывая лишние килограммы рост человека также уменьшался. Корреляционная связь лишь говорит о взаимосвязанности данных параметров, причем в данной конкретной выборке, в другой выборке мы можем не наблюдать полученные корреляции.
При положительной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному увеличению (или уменьшению) другой переменной т.е. взаимосвязи типа увеличение-увеличение (уменьшение-уменьшение).
При отрицательной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному уменьшению (или увеличению) другой переменной т.е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).
Корреляция (синонимы): соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие.
19. Линейный коэффициент корреляции
Эта тема планировалась более 10 лет назад и вот, наконец, я здесь…. И вы здесь! И это замечательно! Даже не то слово. Это корреляционно.
О корреляции речь зашла в статьях в статьях об аналитической и комбинационной группировке, в результате чего перед нами нарисовались некоторые эмпирические показателями корреляции (прочитайте хотя бы «по диагонали»!). И сейчас на очереди линейный коэффициент корреляции, популярный настолько, что по умолчанию под коэффициентом корреляции понимают именно его. …Да, всё верно – существует довольно много разных коэффициентов корреляции. Однако всему своё время.
Материал данной темы состоит из двух уровней:
– начального, для всех – вплоть до студенток психологических и социологических факультетов, школьников, бабушек, дедушек, etc и
– продвинутого, где я разберу более редкие задачи, а некоторые даже не буду разбирать 🙂
В результате вы научитесь БЫСТРО решать типовые задачи (видео прилагается) и для самых ленивых есть калькуляторы. И пока не запамятовал, хочу порекомендовать корреляционно-регрессионный анализ для ваших научных работ и практических исследований – наряду со статистическими гипотезами, это самая настоящая находка в плане новизны и творческих изысканий.
Оглавление:
то было для «чайников», для начала достаточно…
…и в этот момент я благоговейно улыбаюсь – как здорово, что все мы здесь сегодня собрались:
Имеются выборочные данные по 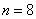
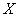
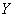
И сразу обращаю внимание, что в условии приведены несгруппированные данные. Помимо этого варианта, есть задачи, где изначально дана комбинационная таблица, и их мы тоже разберём. Сначала одно, затем другое.
1) высказать предположение о наличии и направлении корреляционной зависимости признака-результата 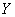
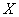
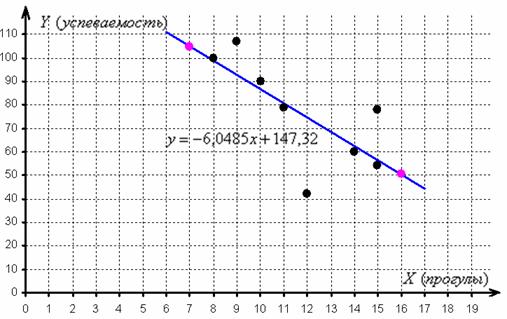
2) анализируя диаграмму рассеяния, сделать вывод о форме зависимости;
3) найти уравнение линейной регрессии 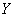
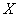
4) вычислить линейный коэффициент корреляции, сделать вывод;
5) вычислить коэффициент детерминации, сделать вывод,
и позже будет ещё 5-6 пунктов для продвинутых читателей (см. конец урока).
Решение:
1) Прежде всего, повторим, что такое корреляционная зависимость. Очевидно, что чем больше студент прогуливает, тем более вероятно, что у него плохая успеваемость. Но всегда ли это так? Нет, не всегда. Успеваемость зависит от многих факторов. Один студент может посещать все пары, но все равно учиться посредственно, а другой – учиться неплохо даже при достаточно большом количестве прогулов. Однако общая тенденция состоит в том, что с увеличением количества прогулов средняя успеваемость студентов будет падать. Такая нежёсткая зависимость и называется корреляционной.
По своему направлению зависимость бывает прямой («чем больше, тем больше») и обратной («чем больше, тем меньше»). В данной задаче мы высказали предположение о наличии обратной корреляционной зависимости 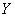
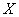
Проверить выдвинутое предположение проще всего графически, и в этом нам поможет:
диаграмма рассеяния
– это множество точек 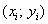
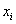
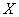
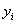
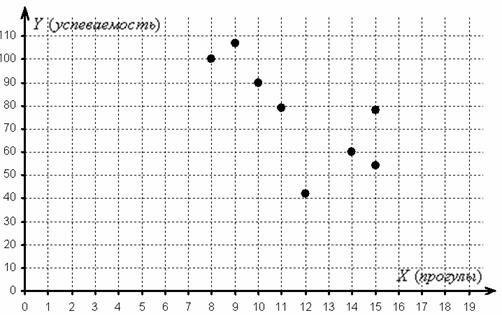
Обратите, кстати, внимание как раз на тот момент, что при одном и том же количестве прогулов (15) двое студентов имеют существенно разные результаты.
2) По диаграмме рассеяния хорошо видно, что с увеличением числа прогулов успеваемость преимущественно падает, что подтверждает наличие обратной корреляционной зависимости успеваемости от количества прогулов. Более того, почти все точки «выстроились» примерно по прямой, что даёт основание предположить, что данная зависимость близкА к линейной.
И здесь я анонсирую дальнейшие действия: сейчас нам предстоит найти уравнение прямой, ТАКОЙ, которая проходит максимально близко сразу ко всем эмпирическим точкам, а также оценить тесноту линейной корреляционной зависимости – насколько близко расположены эти точки к построенной прямой.
Технически существует два пути решения:
– сначала найти уравнение прямой и затем оценить тесноту зависимости;
– сначала найти тесноту и затем составить уравнение.
В практически задачах чаще встречается второй вариант, но я начну с первого, он более последователен. Построим:
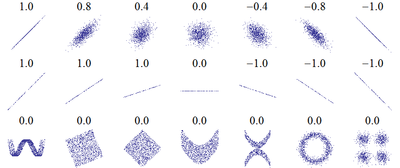
3) уравнение линейной регрессии  на
на 
Это и есть та самая оптимальная прямая 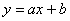
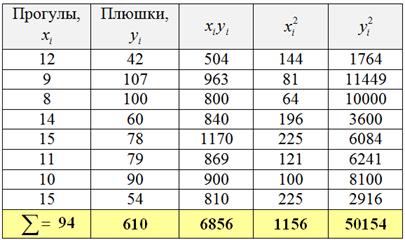
Обратите внимание, что в отличие от задач урока МНК у нас появился дополнительный столбец 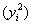
Коэффициенты функции 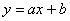
Сократим оба уравнения на 2, всё попроще будет:
Систему решим по формулам Крамера: 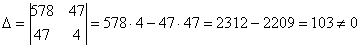
И проверка forever, подставим полученные значения 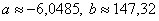
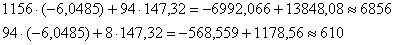
в результате получены соответствующие правые части, значит, система решена верно.
Таким образом, искомое уравнение регрессии:
Данное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а». И обратите особое внимание, что эта функция возвращает нам средние (среднеожидаемые) значения «игрек» для различных значений «икс».
Почему это регрессия именно « 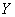
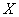
Найдём пару удобных точек для построения прямой: 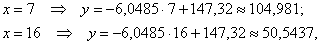
отметим их на чертеже (малиновый цвет) и проведём линию регрессии:
Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью него можно интерполировать (восстановить) неизвестные промежуточные значения, так при количестве прогулов 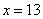
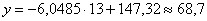
И, конечно, осуществимо прогнозирование, так при 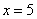
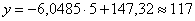
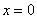
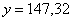
Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе эмпирические точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак 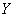
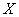
Прояснить данный вопрос нам поможет:
4) линейный коэффициент корреляции
Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной корреляции Пирсона 🙂
– «выборочный» – потому что мы рассматриваем выборочную совокупность;
– «линейный» – потому что он оценивает тесноту линейной корреляционной зависимости;
– «пАрной» – потому что у нас два признака (бывает хуже);
– и «Пирсона» – в честь английского статистика Карла Пирсона, это он автор понятия «корреляция».
И в зависимости от фантазии автора задачи вам может встретиться любая комбинация этих слов. Теперь нас не застанешь врасплох, Карл.
Линейный коэффициент корреляции вычислим по формуле: 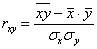
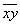
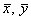
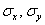
Осталось разгрести всё это добро 🙂 Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние значения:
Стандартные отклонения найдём как корни из соответствующих дисперсий, вычисленных по формуле:
Таким образом, коэффициент корреляции:
И расшифровка: коэффициент корреляции может изменяться в пределах 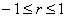
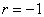
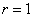
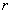
Для оценки тесноты связи будем использовать уже знакомую шкалу Чеддока: 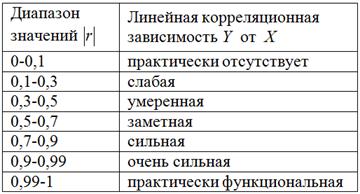
При этом если 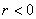
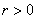
В нашем случае 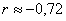
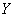
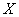
Линейный коэффициент корреляции – это частный аналог эмпирического корреляционного отношения. Но в отличие от отношения, он показывает не только тесноту, но ещё и направление зависимости, ну и, конечно, здесь определена её форма (линейная).
5) Коэффициент детерминации
– это частный аналог эмпирического коэффициента детерминации – есть квадрат коэффициента корреляции:
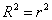
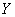
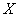
В нашей задаче:
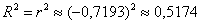
! Примечание: но это не является какой-то «абсолютной истиной», это всего лишь оценка в рамках построенной модели.
Задание выполнено
Но точку ставить рано. Теперь второй способ решения, в котором мы сначала находим коэффициент корреляции, а затем уравнение регрессии.
Линейный коэффициент корреляции вычислим по формуле: 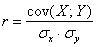
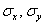
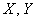
Член в числителе называют корреляционным моментом или коэффициентом ковариации (совместной вариации) признаков, он рассчитывается следующим образом: 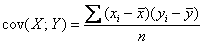
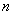
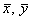
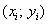
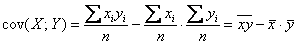
Заполним расчётную таблицу: 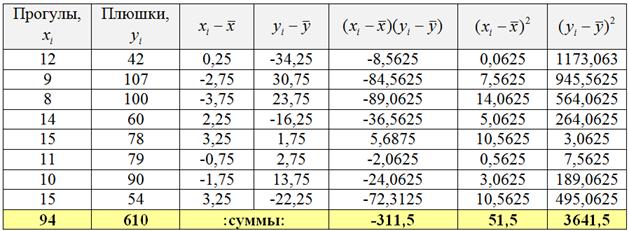
При этом сначала рассчитываем левые нижние суммы и средние значения признаков:
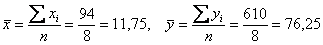
Вычислим коэффициент ковариации: 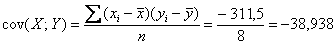
Стандартные отклонения вычислим как квадратные корни из дисперсий:
Таким образом, коэффициент корреляции:
И если нам известны значения 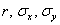
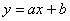
Таким образом, искомое уравнение:
Теперь смотрим ролик о том, как это всё быстро подсчитать и построить:

Если под рукой нет Экселя, ничего страшного, разобранную задачу не так трудно решить в обычной клетчатой тетради. А если Эксель есть и времени нет, то можно воспользоваться моим калькулятором. Да, вы можете найти аналоги в Сети, но, скорее всего, это будет не совсем то, что нужно 😉
Какой способ решения выбрать? Ориентируйтесь на свой учебный план и методичку. По умолчанию лучше использовать 2-й способ, он несколько короче, и, вероятно, потому и встречается чаще. Кстати, если вам нужно построить ТОЛЬКО уравнение регрессии, то уместен 1-й способ, ибо там мы находим это уравнение в первую очередь.
Следующая задача много-много лет назад была предложена курсантам местной школы милиции (тогда ещё милиции), и это чуть ли не первая задача по теме, которая встретилась в моей профессиональной карьере. И я безмерно рад предложить её вам сейчас, разумеется, с дополнительными пунктами:)
В результате 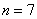

…да, числа могут быть и отрицательными.
По данным наблюдений вычислить линейный коэффициент корреляции и детерминации, сделать выводы. Найти параметры линейной регрессии 
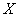
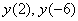
Из условия следует, что признак 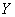
Все данные уже забиты в Эксель, и вам осталось аккуратно выполнить расчёты. В образце я решил задачу вторым, более распространённым способом. И, конечно же, выполните проверку первым путём.
Следует отметить, что в целях экономии места я специально подобрал задачи с малым объёмом выборки. На практике обычно предлагают 10 или 20 пар чисел, реже 30, и максимальная выборка, которая мне встречалась в студенческих работах – 100. …Соврал малость, 80.
И сейчас я вас приглашаю на следующий урок, назову его Уравнение линейной регрессии, где мы рассчитаем и найдём всё то же самое – только для комбинационной группировки. Плюс немного глубже копнём уравнения регрессии (их два).
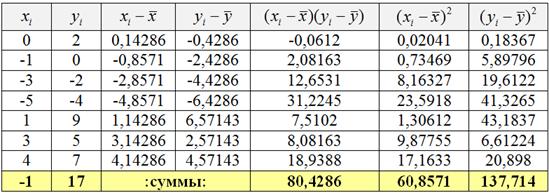
Пример 68. Решение: вычислим суммы и средние значения признаков 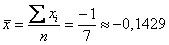
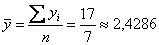
Вычислим коэффициент ковариации: 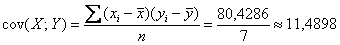
Вычислим средние квадратические отклонения:
Вычислим коэффициент корреляции: 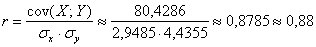
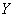
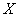
Вычислим коэффициент детерминации:
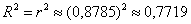
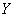
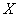
Вычислим коэффициенты линейной регрессии 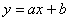
Таким образом, искомое уравнение регрессии:
Данное уравнение показывает, что с увеличением значения «икс» на одну единицу «игрек» увеличивается в среднем примерно на 1,32 единицы (смысл коэффициента «а»).
При 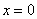
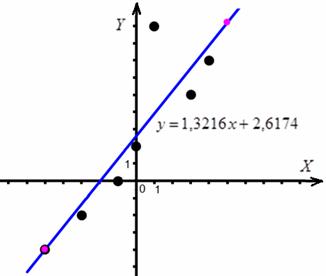
Найдём пару точек для построения прямой: 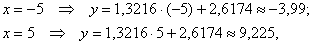
и выполним чертёж:
Вычислим:
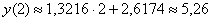
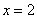
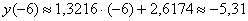
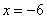
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5


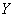 на
на