гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке
Гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке
Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.
1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.
2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.
3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.
5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.
Переведем скорость
Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.
1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).
2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.
3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно
Значит, Р = 15 кН.
4. Верно. (см. пункт 3).
5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).
Скорость гоночной машины
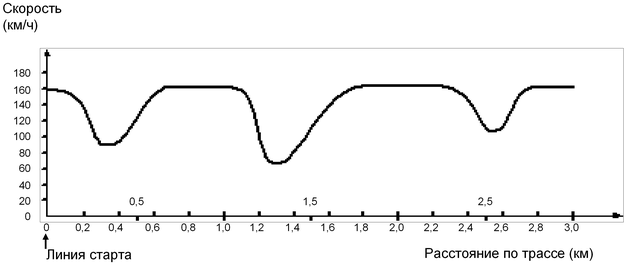
На графике показано, как изменялась скорость гоночной машины, когда она проходила второй круг по трехкилометровой кольцевой трассе без подъемов и спусков.
Вопрос 1. Чему примерно равно расстояние от линии старта до начала самого длинного прямолинейного участка трассы?
| A. | 0,5 км | B. | 1,5 км | C. | 2,3 км | D. | 2,6 км |
Решение. При выезде на прямолинейный участок трассы машина сначала разгоняется до максимальной скорости, затем продолжает движение с набранной скоростью и в конце участка машина притормаживает, чтобы вписаться в поворот. Причем, чем длиннее прямолинейный участок, тем больше продолжается движение с максимальной скоростью.
Из графика видно, что дольше всего максимальная скорость сохранялась между 1,8 и 2,3 км. Значит, эта часть графика соответствует самому длинному прямолинейному участку трассы, начало которого, выбирая из предложенных вариантов, находится в 1,5 км от линии старта.
Правильный ответ: B.
Вопрос 2. В каком месте трассы скорость машины была наименьшей при прохождении второго круга?
| A. | На линии старта. | B. | Примерно на отметке 0,8 км. |
| C. | Примерно на отметке 1,3 км. | D. | Примерно посередине трассы. |
Решение. Из графика видно, что наименьшая скорость машины при прохождении второго круга, равная 70 км/ч, была примерно на отметке 1,3 км.
Правильный ответ: C.
Вопрос 3. Что можно сказать о скорости машины при прохождении трассы между отметками 2,6 км и 2,8 км?
| A. | Скорость машины оставалась постоянной. |
| B. | Скорость машины увеличивалась. |
| C. | Скорость машины уменьшалась. |
| D. | По данному графику невозможно определить изменение скорости машины. |
Решение. Из Из графика видно, что скорость машины на этом участке увеличивалась со 110 до 160 км/ч.
Правильный ответ: B.
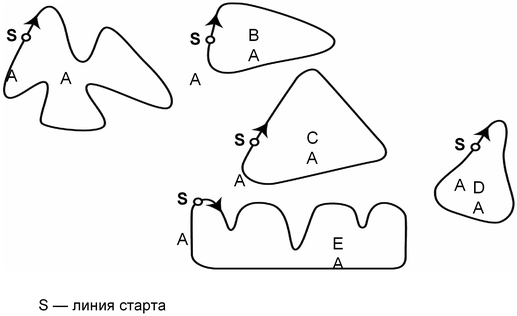
Вопрос 4. Ниже изображены пять различных по форме гоночных трасс:
По какой из этих трасс ехала гоночная машина, график скорости которой приведен ранее?
Решение. Судя по графику скорости, трасса содержит три прямолинейных участка: точка старта находится на самом коротком из них, далее идет средний по длине участок и затем самый длинный. Минимальная скорость у машины между средним и длинным участками, значит, между ними должен быть самый крутой поворот. Данным требованиям удовлетворяет форма трассы B.
Правильный ответ: B.
Гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке
На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из автомобилей за первые 15 с движения проехал наибольший путь. Найдите этот путь. Ответ выразите в метрах.
Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). Из приведенного рисунка видно, что максимальная площадь под графиком за первые 15 с, а значит, и максимальный путь на этом интервале времени, у автомобиля 3.
Найдём его путь, используя формулу для площади трапеции:
Извините, а как определить площадь под графиком 4?
В данной задаче нет необходимости ее подсчитывать, поскольку нас просят только сравнить пути (площади). Ясно, что для 4 площадь минимальна. Ежели поставить целью посчитать площадь, то это можно сделать приблизительно, посчитав по клеточкам (даже можно оценить погрешность такого подсчета).
То есть тут в принципе только визуальная составляющая работает?как то в точных науках так на глаз оценивать достаточно не привычно, но в тоже время легче.
В некотором роде любой эксперимент — это оценивание величин «на глаз». Когда Вы что-то измеряете линейкой, Вы смотрите, какое из делений ближе всего 🙂
Ускорение каждого можно найти по формуле a=(V1-V0)/t
Задачи
1. Средняя скорость из А в В.
Расстояние от пункта А до пункта В равно 45 км. Первую часть пути автомобиль ехал со скоростью в два раза меньше средней, а вторую часть пути – со скоростью в два раза больше средней. Найдите длину первой части пути.
2.Опять средняя скорость
Треть всего пути автомобиль проехал с постоянной скоростью V1, затем треть всего времени он ехал с постоянной скоростью V2. Найдите среднюю скорость на всем пути, если она оказалась равна скорости на оставшемся участке.
Ответ: 
На рисунке приведен план гоночной трассы гонок. Длины участков трассы: L1 = 1,8 км, L2 = 1,0 км, L3 = 1,4 км, L4 = 1,2 км. Каждый гоночный автомобиль (болид) движется на соответствующих участках трассы со скоростями: V1 = 60 м/с, V2 = 50 м/с, V3 = 20 м/с, V4 = 40 м/с. При переходе машины с одного участка на другой ее скорость изменяется практически мгновенно. По правилам заезда расстояние вдоль трассы между болидами не должно быть меньше L0 = 200 м. Какое максимальное число n автомобилей может одновременно участвовать в гонке?
Два электромеханических зайца соревнуются в беге. Один из них питается от обычной батарейки, а другой от «Duraell». Заяц с обычной батарейкой прибежал к финишу на t1 = 6 с позже своего соперника. Тогда ему заменили обычную батарейку на «Energizer». Во втором забеге зайцы побежали по той же трассе. С новой батарейкой скорость зайца возросла в полтора раза, и он прибежал к финишу на t2 = 8 с раньше соперника. Найдите отношение скорости V2 второго зайца к скорости V1 первого зайца во время первого забега.
Ответ:
5. Встречные поезда
Поезд-экспресс прошел за время t1 = 9 с мимо встречной электрички, двигавшейся с такой же скоростью и имевшей в два раза большую длину. За какое время t2 экспресс пройдет мимо встречного пассажирского поезда, который в два раза длиннее электрички и едет вдвое быстрее?
6. Две радиоуправляемые машинки ездят по прямолинейному полигону. Их скорости зависят от времени периодически (рис.). В момент времени t = 0 машины находились рядом. На какое максимальное расстояние S они удалятся друг от друга в процессе движения?
7.Средняя скорость из А в В и обратно
Из города А в город В автомобилист ехал с постоянной скоростью 80 км/ч. На обратном пути трасса была загружена, и он двигался со скоростью 30 км/ч столько же времени, сколько он затратил на движение в первой поездке, а вот отставшийся участок пути оказался свободным, и автомобиль двигался со скоростью 100 км/ч. Определите среднюю скорость автомобиля на всем пути от города А до В и обратно.
8. Звуковые сигналы
Два гоночных автомобиля мчатся навстречу друг другу с одинаковой скоростью. Один из водителей начинает подавать звуковые сигналы длительностью V1, при этом другой водитель определил их длительностью V2 = 0,8V1. Скорость звука c в воздухе постоянна и равна 333 м/с. С какой скоростью едут автомобили?
9.Встреча поезда с электричкой
Длинный поезд едет со скоростью V. По соседним путям его обгоняет электричка, скорость которой 72 км/ч. Машиниста электрички заметил, что он проехал мимл поезда за 100 с. На обратном пути электричка и поезд снова встретились. На этот раз оказалось, что время прохождения электрички мимо поезда равно 20 с. Какова скорость поезда?
10. Средняя скорость.
Автомобиль первую половину времени ехал со скоростью V1 = 80 км/ч, оставшееся время – со скоростью V2 = 40 км/ч. Найдите среднюю скорость автомобиля на второй половине его пути.
Две машины едут по прямому участку дороги навстречу друг другу. Графики зависимости ско-ростей машин от времени приве-дены на рисунках 1 и 2. Чему равна средняя скорость сближения машин за первые 10 минут? Считайте, что машины сначала были на очень большом расстоянии и не успели встретиться. Указание: средняя скорость сближения – это отношение изменения расстояния между машинами ко времени движения машин.
Мальчик смог переплыть реку за минимальное время. Ширина реки равна 100 м. Скорость мальчика относительно воды постоянна и равна 1 м/с. Зависимость скорости течения V от расстояния х до берега приведена на графике. На какое расстояние вниз по реке его снесло течением? Считать, что в любом месте реки скорость течения направлена вдоль берегов.
13.Среднее сближение – 2.
Две машины едут по прямолинейному участку дорогу навстречу друг другу. Графики зависимости скоростей машин от пройденного расстяония приведены на рисунках. Вначале расстояние между машинами было равно 20 км.
Чему равна средняя скорость машин до их встречи? С какой максимальной скоростью сближались машины? Сколько времени длилось сближение с максимальной скоростью?
Указание: средняя скорость сближения – это отношение изменения расстояния между машинами ко времени движения машин.
Ответ: 22,2 м/с, 40 м/с, 900 с.
Первую часть пути машина проехала со скоростью 2V, а вторую – со скоростью 
Ответ: 
Крокодил Гена развивает скорость 5 м/с, но пробежать с таком скоростью он может не более 100 метров. После этого у него остаются силы только на последний рывок длиной 10 метров со скоротью 10 м/с. Чебурашка умеет бегать со скоростью V. Какую минимальную дистанцию от крокодила должен соблюдать Чебурашка, чтобы Гена не смог его догнать? Рассмотреть случаи, когда 
16. Время относительно
Поезд проехал мост длиной l = 450 м за t1 = 45 с. Охранник, стоящий на мосту, заметил, что поезд двигался мимо него в течение t2 = 30 с. Какое время ехал по мосту пассажир, сидящий в вагоне поезда? Найдите длину поезда, скорость его движения, и определите во сколько раз длина поезда больше длины моста.
Внедорожник «Нива» может проехать расстояние l = 39 км, имея скорость на асфальте х1 = 100 км/ч, а на грунтовом участке х2 = 25 км/ч. Автомобиль BMW на той же дороге по асфальту разгоняется до х3 = 160 км/ч, но по грунтовке едет только со скоростью х4 = 10 км/ч. При какой длине грунтового участка время движения машин окажется одинаковым?
Гоночный автомобиль проехал трассу так что скорость менялась таким образом как показано на рисунке
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути
км:
Найдём, при каком ускорении автомобиль достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути
км:
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,7 километра. Задача сводится к решению уравнения при известном значении длины пути
км:
Я не понял! Этот гонщик у вас на космическом корабле что ли гоняет?
Все в порядке с ним. Выразите ускорение в метрах в секунду в квадрате, сами убедитесь.
Выразим ускорение из формулы для скорости и найдём его:
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 1,1 км. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км: