гмт что это такое
Газомоторное топливо ГМТ
Природный газ является наиболее универсальным и доступным топливом, способным заменить нефтепродукты. К тому же он имеет целый ряд преиму
ИА Neftegaz.RU. Природный газ является наиболее универсальным и доступным топливом, способным заменить нефтепродукты.
По состоянию на конец 2010 г. в мире действовало более 18 тыс АГНКС; спрос на КПГ за 2010 г. вырос на 20%.
Газпром, являясь лидером газомоторного рынка России:
В настоящее время российский парк автомобилей, работающих на природном газе, оценивается более чем в 86 тыс единиц.
Одной из основных задач, связанных с развитием рынка СПГ для транспортного сектора является увеличение числа автомобилей и судов, использующих СПГ в качестве топлива.
Главные технические вопросы в данной области связаны с разработкой и совершенствованием различных типов двигателей, работающих на СПГ.
Судовые двигатели на СПГ.
Можно выделить 3 технологии СПГ-двигателей:
Двигатели с искровым зажиганием работают только на природном газе, в то время как 2-топливные дизельно-газовые двигатели могут работать на дизельном топливе, СПГ и мазуте.
На сегодняшний день можно выделить 3 основных производителя на данном рынке: Wärtsila, Rolls-Royce и Mitsubishi Heavy Industries.
Во многих случаях существующие дизельные двигатели могут быть преобразованы в 2-топливные дизельно-газовые двигатели.
Подобное преобразование существующих двигателей может быть экономически целесообразным решением перевода морских судов на СПГ.
Автомобильные двигатели для СПГ,
Геометрическое место точек
Геометри́ческое ме́сто то́чек (ГМТ) — фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.
Примеры
Формальное определение
В общем случае, геометрическое место точек формулируется параметрическим предикатом, аргументом которого является точка данного линейного пространства. Параметры предиката могут носить различный тип. Предикат называется детерминантом геометрического места точек. Параметры предиката называются дифференциалами геометрического места точек (не путать с дифференциалом в анализе).
Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.
Если заданы детерминант 
, где 
— точка, 
— дифференциалы, то искомую фигуру 
задают в виде: « — геометрическое место точек , таких, что ». Далее обычно указывается роль дифференциалов, им даются названия применительно к данной конкретной фигуре. Под собственно фигурой понимают совокупность (множество) точек , для которых для каждого конкретного набора значений высказывание обращается в тождество. Каждый конкретный набор значений дифференциалов определяет отдельную фигуру, каждую из которых и всех их в совокупности именуют названием фигуры, которая задаётся через ГМТ.
В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае простых детерминантов, вообще обходятся без буквенных обозначений.
Пример: параболу зададим как множество всех таких точек , что расстояние от до точки 
равно расстоянию от до прямой 
. Тогда дифференциалы параболы — и ; детерминант — предикат 
, где 
— расстояние между двумя точками (метрика), 
— расстояние от точки до прямой. И говорят: «Парабола — геометрическое место точек , равноудалённых от точки и прямой . Точку называют фокусом параболы, а прямую — директрисой».
Геометрическое место точек
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Понятие ГМТ часто используют при решении задач на построение.
Гмт что это такое
Смотреть что такое «ГМТ» в других словарях:
гмт — сущ., кол во синонимов: 1 • гексаметилентетрамин (3) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ГМТ — … Википедия
НИИ ГМТ — НИИГМТ НИИ ГМТ Научно иследовательский институт гигиены морского транспорта мед., морск., образование и наука НИИГМТ Источник: http://infopravo.by.ru/fed1991/ch03/akt14363.shtm … Словарь сокращений и аббревиатур
Список систем интерактивной геометрии — Содержание 1 Сравнение интерактивных геометрических систем 1.1 Лицензиро … Википедия
GMT — (Географическое время) Понятие GMT(Greenwich Mean Time), среднее географическое время, часовые пояса Информация о GMT (Greenwich Mean Time) CГВ (среднее Географическое (Гринвическое) время), часовые пояса Содержание Содержание Определения… … Энциклопедия инвестора
Геомодификаторы трения — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/28 ноября 2012. Пока процесс обсуждени … Википедия
Торговая сессия — (Trading session) Торговая сессия это период времени, в процессе которого совершаются валютные сделки при участии банков и торговых площадок, расположенных в одной географической зоне Определение торговой сессии, индикатор торговых сессий Форекс… … Энциклопедия инвестора
Гмт что это такое
Древнеегипетскую и вавилонскую культуру в области математики продолжали греки. Они не только усвоили весь опыт их геометрии, но и пошли гораздо дальше. Ученые древней Греции сумели привести в систему накопленные геометрические знания и, таким образом, заложить начала геометрии как дедуктивной науки.
Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?
К сожалению, не сохранилось первоисточников, описывающих ранний период развития греческой математики. Только благодаря восстановленным текстам четвертого столетия до нашей эры и трудам арабских ученых, которые были богаты переводами сочинений авторов античной Греции, мы располагаем изданиями Евклида, Архимеда, Аполлония и других великий людей. Но в этих произведениях уже представлена вполне развитая математическая наука.
Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век. Историки науки выделяют три периода ее развития в соответствии с характером знаний:
Геометрическое место точек (ГМТ).
Определения.
Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера. Например: геометрическое место точек, равноудаленных от двух данных точек A и B – это серединный перпендикуляр к отрезку AB. Иногда говорят и о геометрическом месте прямых и других фигур.
Название связано с представлением о линии как о «месте», на котором располагаются точки.
Примеры.
Пример 1.
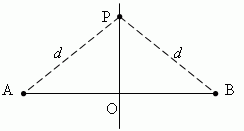
Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO перпендикулярно AB и AO = OB :
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример 2.
Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.
Пример 3.
Окружность есть геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра ( на рис. показана одна из этих точек – А ).
Теоретическая часть.
Касательная. Предположим, секущая PQ ( рис.2 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
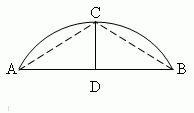
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.4 ). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.
рис. 4
Сектор – это часть круга, ограниченная дугой AmB и двумя радиусами OA и OB, проведенными к концам этой дуги ( рис.5 ).
Центральный угол – угол, образованный двумя радиусами ( ∠AOB, рис.5 ). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки ( ∠BAC, рис.4 ). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( ∠BAC, рис.3 ).
Соотношения между элементами круга.
Вписанный угол ( ∠ABC, рис.7 ) равен половине центрального угла, опирающегося на ту же дугу AmC ( ∠AOC, рис.7 ). Поэтому, все вписанные углы ( рис.7 ), опирающиеся на одну и ту же дугу ( AmC, рис.7 ), равны. А так как центральный угол содержит то же количество градусов, что и его дуга ( AmC, рис.7 ), то любой вписанный угол измеряется половиной дуги, на которую он опирается ( в нашем случае AmC ).
Все вписанные углы, опирающиеся на полукруг (∠APB, ∠AQB, …, рис.8 ), прямые.
Угол (∠AOD, рис.10), образованный двумя секущими ( AO и OD ), измеряется полуразностью дуг, заключённых между его сторонами: ( AnD – BmC ) / 2.
Угол (∠DCB, рис.11), образованный касательной и хордой ( AB и CD ), измеряется половиной дуги, заключённой внутри него: CmD / 2.
Произведения отрезков хорд ( AB и CD, рис.13 или рис.14), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO.
Квадрат касательной равен произведению секущей на её внешнюю часть ( рис.12): OA 2 = OB · OD. Это свойство можно рассматривать как частный случай рис.14.
Интересный факт:
Поздравляем с Пи-раздником вас.
Фанаты будут соревноваться, вспоминая знаки числа «Пи». И постараются превзойти рекорд 24-летнего китайского студента Лю Чао, который назвал по памяти без ошибок 68890 знаков. На это у него ушло 24 часа и 4 минуты.
Отмечать праздник придумал американский физик Ларри Шо (Larry Shaw).
На вопрос, сколько знаков в числе «Пи» после запятой, точного ответа нет. Скорее всего, их бесконечное число. А главная особенность в том, что последовательность этих знаков не повторяется. Сегодня их известно 12411 триллионов. Обследовано 500 миллиардов. И повторений не найдено.
Список использованных источников:
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.