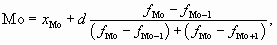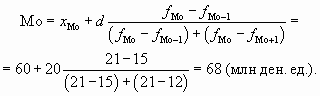чему равна мода вариационного ряда
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
где х о – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1 – частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе – порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число | ||||
| До 5000 | 600 | 600 | 6 | ||
| 5000-6000 | 700 | 1300 (600+700) | 13 | ||
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 ) (хо) | 2500 (fМе) | 5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 | ||
| 9000-10000 | 1500 | 9200 | 92 | ||
| Свыше 10000 | 800 | 10000 | 100 | ||
| Итого | 10000 | – | – |
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если М о о следует сделать вывод о левосторонней асимметрии ряда.
Структурные характеристики вариационного ряда распределения
8.1. Мода
8.1.1. Определение моды в дискретных вариационных рядах
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
Подставив в формулу соответствующие величины, получим
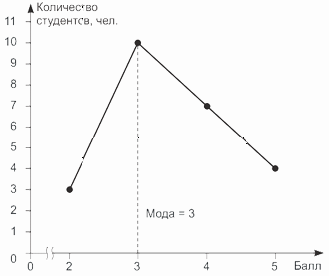
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).
Структурные характеристики вариационного ряда распределения
8.1. Мода
8.1.1. Определение моды в дискретных вариационных рядах
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
Подставив в формулу соответствующие величины, получим
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).
Мода в статистике
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Как найти моду если числа не повторяются. Статистика
Мода и медиана – особого рода средние, которые используются для изучения структуры вариационного ряда. Их иногда называют структурными средними, в отличие от рассмотренных ранее степенных средних.
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.
Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.
Медиана – это варианта, которая находится в середине упорядоченного вариационного ряда.
Медиана показывает количественную границу значения варьирующего признака, которой достигла половина единиц совокупности. Применение медианы наряду со средней или вместо нее целесообразно при наличии в вариационном ряду открытых интервалов, т.к. для вычисления медианы не требуется условное установление границ отрытых интервалов, и поэтому отсутствие сведений о них не влияет на точность вычисления медианы.
Медиану применяют также тогда, когда показатели, которые нужно использовать в качестве весов, неизвестны. Медиану применяют вместо средней арифметической при статистических методах контроля качества продукции. Сумма абсолютных отклонений варианты от медианы меньше, чем от любого другого числа.
Рассмотрим расчет моды и медианы в дискретном вариационном ряду:
Определить моду и медиану.
Мода Мо = 4 года, так как этому значению соответствует наибольшая частота f = 5.
Т.е. наибольшее число рабочих имеют стаж 4 года.
Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.
Т.е. половина рабочих имеет стаж меньше четырех лет, половина больше.
Если сумма накопленных частот против одной варианты равна половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Вычисление моды и медианы в интервальном вариационном ряду
Мода в интервальном вариационном ряду вычисляется по формуле
h м 0 – величина модального интервала,
f м 0 , f м 0-1 , f м 0+1 – частота соответственно модального интервала, предшествующего модальному и последующего.
Модальным называется такой интервал, которому соответствует наибольшая частота.
Определить моду и медиану.
Посмотреть решение задачи на нахождение моды и медианы Вы можете
В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:
Свойства медианы
Графическое определение медианы
Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.
Определение моды в статистике
Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.
Нахождение моды и медианы происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле :
Модальный интервал определяется по наибольшей частоте.
Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.
Соотношения между средней арифметической, медианой и модой
К. Пирсон на основе выравнивания различных типов кривых определил, что для умеренно асимметричных распределений справедливы такие приближенные соотношения между средней арифметической, медианой и модой:
При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определённый день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25. При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определённый день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
Среднее арифметическое ряда. Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.():12=27
Размах ряда. Размахом ряда называется разность между наибольшим и наименьшим из этих чисел. Размахом ряда называется разность между наибольшим и наименьшим из этих чисел. Наибольший расход времени равен 37 мин, а наименьший – 18 мин. Найдём размах ряда: 37 – 18 = 19(мин)
Мода ряда. Модой ряда чисел называется число, которое встречается в данном ряду чаще других. Модой ряда чисел называется число, которое встречается в данном ряду чаще других. Модой нашего ряда является число – 25. Модой нашего ряда является число – 25. Ряд чисел может иметь более одной моды, а может не иметь. 1) 47,46,50,47,52,49,45,43,53,53,47,52 – две моды 47 и 52. 2) 69,68,66,70,67,71,74,63,73,72 – моды нет.
Среднее арифметическое, размах и мода, находят применение в статистике – науке, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Среднее арифметическое, размах и мода, находят применение в статистике – науке, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Статистика изучает численность отдельных групп населения страны и её регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т. п. Статистика изучает численность отдельных групп населения страны и её регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т. п.
4. В аттестате о среднем образовании у четырёх друзей – выпускников школы – оказались следующие оценки: Ильин: 4,4,5,5,4,4,4,5,5,5,4,4,5,4,4; Ильин: 4,4,5,5,4,4,4,5,5,5,4,4,5,4,4; Семёнов: 3,4,3,3,3,3,4,3,3,3,3,4,4,5,4; Семёнов: 3,4,3,3,3,3,4,3,3,3,3,4,4,5,4; Попов: 5,5,5,5,5,4,4,5,5,5,5,5,4,4,4; Попов: 5,5,5,5,5,4,4,5,5,5,5,5,4,4,4; Романов: 3,3,4,4,4,4,4,3,4,4,4,5,3,4,4. Романов: 3,3,4,4,4,4,4,3,4,4,4,5,3,4,4. С каким средним баллом окончил школу каждый из этих выпускников? Укажите наиболее типичную для каждого из них оценку в аттестате. Какие статистические характеристики вы использовали при ответе? С каким средним баллом окончил школу каждый из этих выпускников? Укажите наиболее типичную для каждого из них оценку в аттестате. Какие статистические характеристики вы использовали при ответе?
Самостоятельная работа Вариант 1. Вариант Дан ряд чисел: 35, 44, 37, 31, 41, 40, 31, 29. Найдите среднее арифметическое, размах и моду рада. 2. В ряду чисел 4, 9, 16, 31, _, 25 4, 9, 16, 31, _, 25 пропущено одно число. пропущено одно число. Найдите его, если: Найдите его, если: а) среднее арифметичес- а) среднее арифметичес- кое равно 19; кое равно 19; б) размах ряда – 41. б) размах ряда – 41. Вариант Дан ряд чисел: 38, 42, 36, 45, 48, 45,45, 42. Найдите среднее арифметическое, размах и моду рада. 2. В ряду чисел 5, 10, 17, 32, _, 26 пропущено одно число. Найдите его, если: а) среднее арифметичес- кое равно 19; б) размах ряда – 41.
Медианой упорядоченного ряда чисел с нечётным числом чисел называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом чисел называется среднее арифметическое двух чисел, записанных посередине. Медианой упорядоченного ряда чисел с нечётным числом чисел называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом чисел называется среднее арифметическое двух чисел, записанных посередине. В таблице показан расход электроэнергии в январе жильцами девяти квартир: В таблице показан расход электроэнергии в январе жильцами девяти квартир: Номерквартиры Расходэлектро-энергии
Составим упорядоченный ряд: 64, 72, 72, 75, 78, 82, 85, 91,93. 64, 72, 72, 75, 78, 82, 85, 91, – медиана данного ряда. 78 – медиана данного ряда. Дан упорядоченный ряд: Дан упорядоченный ряд: 64, 72, 72, 75, 78, 82, 85, 88, 91, 93. ():2 = 80 – медиана. ():2 = 80 – медиана.
1. Найдите медиану ряда чисел: а) 30, 32, 37, 40, 41, 42, 45, 49, 52; а) 30, 32, 37, 40, 41, 42, 45, 49, 52; б) 102, 104, 205, 207, 327, 408, 417; б) 102, 104, 205, 207, 327, 408, 417; в) 16, 18, 20, 22, 24, 26; в) 16, 18, 20, 22, 24, 26; г) 1,2, 1,4, 2,2, 2,6, 3,2, 3,8, 4,4, 5,6. г) 1,2, 1,4, 2,2, 2,6, 3,2, 3,8, 4,4, 5,6. 2. Найдите среднее арифметическое и медиану ряда чисел: а) 27, 29, 23, 31,21,34; а) 27, 29, 23, 31,21,34; б) 56, 58, 64, 66, 62, 74; б) 56, 58, 64, 66, 62, 74; в) 3,8, 7,2, 6,4, 6,8, 7,2; в) 3,8, 7,2, 6,4, 6,8, 7,2; г) 21,6, 37,3, 16,4, 12, 6. г) 21,6, 37,3, 16,4, 12, 6.
3. В таблице показано число посетителей выставки в разные дни недели: Найдите медиану указанного ряда данных. В какие дни недели число посетителей выставки было больше медианы? Днинедели Пн Пн Вт Вт Ср Ср Чт Чт Пт Пт Сб Сб Вс Вс Число посетите лей
4.Ниже указана среднесуточная переработка сахара (в тыс.ц) заводами сахарной промышленности некоторого региона: (в тыс.ц) заводами сахарной промышленности некоторого региона: 12,2, 13,2, 13,7, 18,0, 18,6, 12,2, 18,5, 12,4, 12,2, 13,2, 13,7, 18,0, 18,6, 12,2, 18,5, 12,4, 14, 2, 17,8. 14, 2, 17,8. Для представленного ряда найдите среднее арифметическое, моду, размах и медиану. Для представленного ряда найдите среднее арифметическое, моду, размах и медиану. 5. В организации вели ежедневный учёт поступивших в течение месяца писем. В результате получили такой ряд данных: 39, 43, 40, 0, 56, 38, 24, 21, 35, 38, 0, 58, 31, 49, 38, 25, 34, 0, 52, 40, 42, 40, 39, 54, 0, 64, 44, 50, 38, 37, 43, 40, 0, 56, 38, 24, 21, 35, 38, 0, 58, 31, 49, 38, 25, 34, 0, 52, 40, 42, 40, 39, 54, 0, 64, 44, 50, 38, 37, 32. Для представленного ряда найдите среднее арифметическое, моду, размах и медиану. Для представленного ряда найдите среднее арифметическое, моду, размах и медиану.
Домашнее задание. На соревнованиях по фигурному катанию выступление спортсмена было оценено следующими баллами: На соревнованиях по фигурному катанию выступление спортсмена было оценено следующими баллами: 5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3. 5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3. Для полученного ряда чисел найдите среднее арифметическое, размах и моду. Для полученного ряда чисел найдите среднее арифметическое, размах и моду.
На тему: «Мода. Медиана. Способы их расчета»
Средние величины и связанные с ними показатели вариации играют в статистике очень большую роль, что обусловлено предметом ее изучения. Поэтому данная тема является одной из центральных в курсе.
Средняя является очень распространенным обобщающим показателям в статистике. Это объясняется тем, что только с помощью средней можно охарактеризовать совокупность по количественно варьирующему признаку. Средней величиной в статистике называется обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку. Средняя показывает уровень этого признака, отнесенный к единице совокупности.
Изучая общественные явления и стремясь выявить их характерные, типичные черты в конкретных условиях места и времени, статистики широко используют средние величины. С помощью средних можно сравнивать между собой различные совокупности по варьирующим признакам.
Средние, которые применяются в статистике, относятся к классу степенных средних. Из степенных средних наиболее часто применяется средняя арифметическая, реже – средняя гармоническая; средняя гармоническая применяется только при исчислении средних темпов динамики, а средняя квадратическая – только при исчислении показателей вариации.
Средняя арифметическая есть частное от деления суммы вариант на их число. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных ее единиц. Средняя арифметическая – наиболее распространенный вид средних, так как она соответствует природе общественных явлений, где объем варьирующих признаков в совокупности чаще всего образуется именно как сумма значений признака у отдельных единиц совокупности.
По своему определяющему свойству средняя гармоническая должна применяться тогда, когда общий объем признака образуется как сумма обратных значений вариант. Ее применяют тогда, когда в зависимости от имеющего материала веса приходиться не умножать, а делить на варианты или, что то же самое, умножать на обратное их значение. Средняя гармоническая в этих случаях – это величина обратная средней арифметической из обратных значений признака.
К средней гармонической следует прибегать в тех случаях, когда в качестве весов применяются не единицы совокупности – носители признака, а произведения этих единиц на значение признака.
1. Определение моды и медианы в статистике
Средние арифметическая и гармоническая являются обобщающими характеристиками совокупности по тому или иному варьирующему признаку. Вспомогательными описательными характеристиками распределения варьирующего признака являются мода и медиана.
Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Медианной в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.
Мода и медиана в отличии от степенных средних являются конкретными характеристиками, их значение имеет какая-либо конкретная варианта в вариационном ряду.
Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака. Если надо, например, узнать наиболее распространенный размер заработной платы на предприятии, цену на рынке, по которой было продано наибольшее количество товаров, размер ботинок, пользующийся наибольшим спросом у потребителей, и т.д., в этих случаях прибегают к моде.
Медиана интересна тем, что показывает количественную границу значение варьирующего признака, которую достигла половина членов совокупности. Пусть средняя заработная плата работников банка составила 650000 руб. в месяц. Эта характеристика может быть дополнена, если мы скажем, что половина работников получила заработную плату 700000 руб. и выше, т.е. приведем медиану. Мода и медиана являются типичными характеристиками в тех случаях, когда взяты совокупности однородные и большой численности.
2. Нахождение моды и медианы в дискретном вариационном ряду
Найти моду и медиану в вариационном ряду, где значения признака заданы определенными числами, не представляет большой трудности. Рассмотрим таблицу 1. с распределение семей по числу детей.
Таблица 1. Распределение семей по числу детей
Очевидно, в этом примере модой будет семья, имеющая двоих детей, так как этому значению варианты соответствует наибольшее число семей. Могут быть распределения, где все варианты встречаются одинаково часто, в этом случае моды нет или, иначе, можно сказать, что все варианты одинаково модальны. В других случаях не одна, а две варианты могут быть наибольшей частоты. Тогда будет две моды, распределение будет бимодальным. Бимодальные распределения могут указывать на качественную неоднородность совокупности по исследуемому признаку.
Чтобы найти медиану в дискретном вариационном ряд, нужно сумму частот разделить пополам и к полученному результату добавить ½. Так, в распределении 185 семьи по числу детей медианой будет: 185/2 + ½ = 93, т.е. 93-я варианта, которая делит упорядоченный ряд пополам. Каково же значение 93-ей варианты? Для того чтобы это выяснить, нужно накапливать частоты, начиная, от наименьшей варианты. Сумма частот 1-й и 2-й вариант равна 40. Ясно, что здесь 93 варианты нет. Если прибавить к 40 частоту 3-й варианты, то получим сумму, равную 40 + 75 = 115. Следовательно, 93-я варианта соответствует третьему значению варьирующего признака, и медианой будет семья, имеющая двоих детей.
Мода и медиана в данном примере совпали. Если бы у нас была четная сумма частот (например, 184), то, применяя указанную выше формулу, получим номер медианной варианты, 184/2 + ½ =92,5. Поскольку варианты с дробным номером не существует, полученный результат указывает, что медиана находится посередине между 92 и 93 вариантами.
3. Расчет моды и медианы в интервальном вариационном ряду
Описательный характер моды и медианы связан с тем, что в них не погашаются индивидуальные отклонения. Они всегда соответствуют определенной варианте. Поэтому мода и медиана не требуют для своего нахождения расчетов, если известны все значения признака. Однако в интервальном вариационном ряду для нахождения приближенного значения моды и медианы в пределах определенного интервала прибегают к расчетам.
Для расчета определенного значения модальной величины признака, заключенного в интервале, применяют формулу:
М о = Х Мо + i Мо *(f Мо – f Мо-1)/((f Мо – f Мо-1) + (f Мо – f Мо+1)),
Где Х Мо – минимальная граница модального интервала;
i Мо – величина модального интервала;
f Мо – частота модального интервала;
f Мо-1 – частота интервала, предшествующего модальному;
f Мо+1 – частота интервала, следующего за модальным.
Покажем расчет моды на примере, приведенном в таблице 2.
Таблица 2. Распределение рабочих предприятия по выполнению норм выработки
Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из примера видно, что наибольшая частота соответствует интервалу, где варианта лежит в пределах от 100 до 105. Это и есть модальный интервал. Величина модального интервала равна 5.
Подставляя числовые значения из таблицы 2. в указанную выше формулу, получим:
Смысл этой формулы заключается в следующем: величину той части модального интервала, которую нужно добавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. В данном случае к 100 прибавляем 8,8, т.е. больше половины интервала, потому что частота предшествующего интервала меньше частоты последующего интервала.
Исчислим теперь медиану. Для нахождения медианы в интервальном вариационном ряду определяем сначала интервал, в котором она находится (медианный интервал). Таким интервалом будет такой, комулятивная частота которого равна или превышает половину суммы частот. Комулятивные частоты образуются путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака. Половина суммы частот у нас равна 250 (500:2). Следовательно, согласно таблицы 3. медианным интервалом будет интервал со значением заработной платы от 350000 руб. до 400000 руб.
Таблица 3. Расчет медианы в интервальном вариационном ряду
До этого интервала сумма накопленных частот составила 160. Следовательно, чтобы получить значение медианы, необходимо прибавить еще 90 единиц (250 – 160).
Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых характеристик (мер).
Например, в ряду значении (2 6 6 8 9 9 9 10) модой является 9, потому что 9 встречается чаше любого другого числа.
Мода представляет собой наиболее часто встречающееся значение (в данном примере это 9) а не частоту встречаемости этого значения (в данном примере равную 3).
Моду находят согласно правилам
1. В случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды.
2. Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значении.
Например, в выборке 1 2 2 2 5 5 5 6 частоты рядом расположенных значении 2 и 5 совпадают и равняются 3. Эта частота больше чем частота других значении 1 и 6 (у которых она равна 1).
3) Если два несмежных (не соседних) значения в выборке имеют равные частоты которые больше частот любого другого значения, то выделяют две моды. Например, в ряду 10 11 11 11 12 13 14 14 14 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной.
Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод)
Задача 1. Найдем медиану выборки 9 3 5 8 4 11 13
Задача 2. Найдем медиану выборки 20, 9, 13, 1, 4, 11.
Среднее арифметическое ряда из n числовых значений подсчитывается как
Чтобы показать обманчивость этого показателя, приведём известный пример: в одном купе вагона поместилась бабушка 60 лет с четырьмя внуками: один – 4 года, двое – по 5 лет и один – 6 лет. Среднее арифметическое возраста всех пассажиров этого купе 80/5 = 16. В другом купе расположилась компания молодежи: двое – 15-ти летних, один – 16-летний и двое – 17-летних. Средний возраст пассажиров этого купе так же равен 80/5 = 16. Таким образом, по средним арифметическим пассажиры этих купе не отличаются. Но если обратиться к показателю стандартного отклонения, то окажется, что средний разброс относительно среднего возраста в первом случае окажется 24,6, а во втором случае 1.
Кроме того, среднее оказывается достаточно чувствительным к очень маленьким или очень большим величинам, отличающимся от основных значений измеренных характеристик. Пусть 9 человек имеют доход от 4500 до 5200 тыс долларов в месяц. Величина их среднего дохода равняется 4900 долларов Если же к этой группе добавить человека имеющего доход в 20000 тыс долларов в месяц, то средняя всей группы сместится и окажется равной 6410 долларов, хотя никто из всей выборки (кроме одного человека) реально не получает такой суммы.
Понятно что аналогичное смещение, но в противоположную сторону можно получить и в том случае, если добавить в эту группу человека с очень маленьким годовым доходом.
Разброс (размахом ) выборки – разность между максимальной и минимальной величинами данного конкретного вариационного ряда. Обозначается буквой R.
Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот.
Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный Например, даны две выборки
Дисперсия представляет собой наиболее часто использующуюся меру рассеяния случайной величины (переменной).
Дисперсия – среднее арифметическое квадратов отклонений значений переменной от ее среднего значения