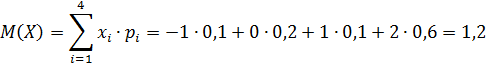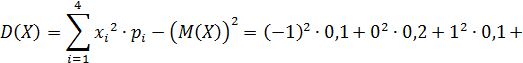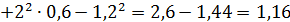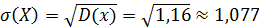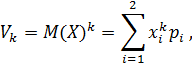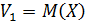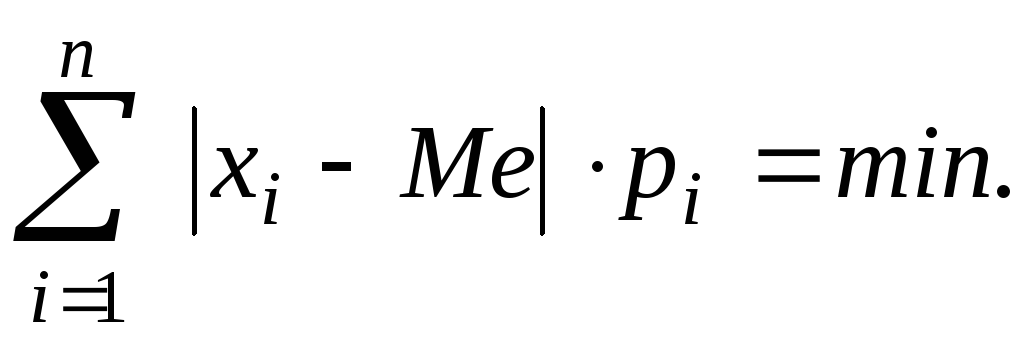чему равна мода случайной величины х

Мода случайной величины.

Модой ( 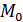(X)) случайной величины называется наиболее вероятное ее значение, то есть значение, вероятность которого максимальна.

Если максимальные вероятности принимают несколько значений случайных величин, то такое распределение называется полимодальным.

Пример.

Дискретная случайная величина X задана законом распределения:

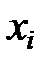	‒1
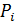	0,1	0,2	0,1	0,6

Найти: числовые характеристики случайной величины:M(X),D(X),Ϭ(X), 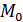(х).

Решение:

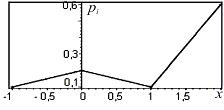
Построим многоугольник распределения данной случайной величины.

1. Математическое ожидание:

3. Средне квадратическое откланение:

4. так как максимальная вероятность этого значения равна 0,6.

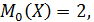
Лекция 6. НАЧАЛЬНЫЕ И ЦЕНТРАЛЬНЫЕ МОМЕНТЫ.

Начальным моментом k‒го порядка называется математическое ожидание k‒й степени случайной величины.

при k=1;

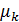
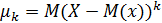
Центральным моментом случайной величины (X) называется математические ожидание k‒й степени отклонения случайной величины (Х) от ее математического ожидания.

,

при k=2, 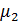=D(Х).

Источник

Числовые характеристики случайных величин

Закон распределения полности характеризует случайную величину. Кроме того, в теории вероятностей широко используются некоторые «типичные значения», которые характеризуют случайную величину суммарно. Эти числа, описывающие некоторые характерные черты распределения, называются числовыми характеристиками.

Важнейшей числовой характеристикой положения случайной величины является математическое ожидание.

1 Математическое ожидание характеризует среднее значение случайной величины, вокруг которого группируются все ее значения. Термин «математическое ожидание» связан с начальным периодом развития теории вероятностей, когда она развивалась на примерах и задачах азартных игр и игрока интересовал средний выигрыш, то есть среднее значение ожидаемого выигрыша. Для дискретных и непрерывных случайных величин математическое ожидание вычисляется, соответственно, по формулам (17) и (18) (при условии, что ряд в формуле (17) и интеграл в формуле (18) сходятся абсолютно):

; (17)

. (18)

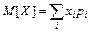
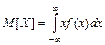
В механической интерпретации математическое ожидание характеризует центр тяжести системы.

Свойства математического ожидания:

а)математическое ожидание постоянной величины равно этой постоянной:

б)постоянный множитель можно выносить за знак математического ожидания:

в)математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий.

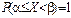
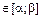
г) если , то M[X] , то есть математическое ожидание произвольной случайной величины X принадлежит интервалу между минимальным и максимальным возможными значениями случайной величины X;

д)математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий. Например, для трех независимых случайных величин X₁, X₂, X₃

2 Модой дискретной случайной величины X (обозначается x_mod) называется ее наиболее вероятное значение, то есть то значение, для которого вероятность p_i достигает максимума. Моду дискретной случайной величины можно определить графически по столбцовой диаграмме, как абсциссу столбца, имеющего наибольшую высоту.

Модой непрерывной случайной величины X (обозначается x_mod) называется то ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два максимума, то распределение называется двумодальным.

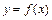
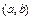
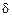
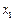
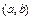
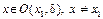
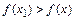
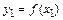
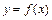
Замечание – Рассмотрим функцию , областью определения которой является промежуток . Если можно указать такую – окрестность точки , принадлежащую промежутку , что для всех , выполняется неравенство , то называют локальным максимумом функции . Максимум функции имеет локальный характер (это наибольшее значение функции в достаточно малой окрестности соответствующей точки).

3 Медианой случайной величины X называется такое ее значение x_med, для которого P(X

Свойства дисперсии:

а)дисперсия постоянной величины равна нулю:

б)постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

в)дисперсия алгебраической суммы нескольких независимых случайных величин равна сумме их дисперсий. Например, для трех случайных величин X₁, X₂ и X₃

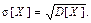
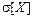
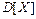
5 Для того чтобы получить характеристику разброса значений случайной величины относительно математического ожидания, имеющую такую же размерность, как и сама случайная величина, используют корень квадратный из дисперсии, взятый с положительным знаком. Полученная величина называется средним квадратическим отклонением (или стандартным отклонением) и обозначается Чем больше разброс значений случайной величины Х вокруг М[Х], тем больше и .

Как следует из определения, размерность дисперсии равна квадрату размерности случайной величины. Так, если случайная величина имеет размерность «вагон», то математическое ожидание, мода и медиана имеют размерность «вагон», дисперсия размерность «вагон 2 », а среднее квадратическое отклонение размерность «вагон».

Часто используются две безразмерные числовые характеристики, описывающие скошенность и островершинность графика функции плотности распределения вероятностей.

6 Коэффициент асимметрии (обозначается A[X]) характеризует скошенность распределения случайной величины относительно математического ожидания. Для симметричных относительно математического ожидания распределений A[X] = 0. Если в распределении случайной величины преобладают положительные отклонения, то A[X] > 0, если отрицательные, то A[X]

Источник

Математическое ожидание и дисперсия. Мода и медиана

Средним значением или математическим ожиданием непрерывной случайной величины X называется значение интеграла

,

где f(x) — плотность вероятности.

Дисперсией непрерывной случайной величины X называется значе­ние интеграла

Дисперсию целесообразно вычислять по формуле

Модой Мо(Х) непрерывной случайной величины X называется такое значение этой величины, плотность вероятности которого максимальна.

Медианой Ме(Х) непрерывной случайной величины X называется та­кое ее значение, при котором выполняется равенство

181. Известно, что число посетителей магазина (в тыс. человек) в день является случайной величиной Х с функцией распределения

.

a. Найти плотность распределения X

b. построить график плотности распределения,

c. Найти вероятность того, что за день магазин посетит от 1 до 2 тысяч человек;

d. Найти вероятность того, что магазин за смену посетит меньше тысячи человек;

e. Найти вероятность того, что число посетителей за смену превысит 2 тысячи человек.

f. Найти математическое ожидание МХ;

g. Найти дисперсию DX.

182. Автобусы подходят к остановке с интервалом в 5 минут. Пусть X – время ожидания автобуса пассажиром.

1) Найти функцию распределения X,

2) Найти плотность распределения X,

3) построить графики функции распределения и плотности распределения,

4) Найти вероятность того, что ;

5) Найти вероятность того, что ;

6) Найти математическое ожидание МХ;

7) Найти дисперсию DX.

183. Известно, что курс ценной бумаги может измениться за день на случайную величину X с плотность распределения

.

a. Найти функцию распределения X

b. построить графики функции распределения и плотности распределения,

c. Найти вероятность того, что курс ценной бумаги повысится;

d. Найти вероятность того, что курс ценной бумаги понизится;

e. Найти математическое ожидание МХ;

f. Найти дисперсию DX.

184. Известно, что время работы некоторого прибора (в годах) является случайной величиной Х с функцией распределения

.

a. Найти плотность распределения X

b. построить графики функции распределения и плотности распределения,

c. Найти вероятность того, что время работы прибора будет от 1 до 3 лет;

d. Найти вероятность того, что прибор проработает больше 5 лет;

e. Найти вероятность того, что прибор проработает меньше 3 лет;

185. Случайная величина X задана функцией распределения вероятностей

1) плотность вероятности f(x) и построить ее график

2) вероятность попадания случайной величины в интервалы [1;2,5], (2,5;3,5).

3) математическое ожидание МХ

186. Функция распределения непрерывной случайной величины X имеет вид:

1) плотность вероятности f(x) и построить ее график

2) математическое ожидание М(X);

4) P(0,6 2 + 2х) в интервале (0; 1). Вне этого интервала f(x)=0. Найти параметр С и MX.

193. Плотность вероятности случайной величины Xимеет вид:

а) найти параметр a;

б) вычислить математическое ожидание;

214. Уровень воды в реке – это нормально распределенная случайная величина со средним значением 2,5 м и стандартным отклонением 20 см. Оценить вероятность того, что в наудачу выбранный день:

а) уровень превысит 3 м; б) окажется в пределах от 2,2 м до 2,8 м.

215. Суточное потребление электроэнергии в населенном пункте является нормально распределенной случайной величиной с математическим ожиданием 2000 кВт/ч и дисперсией 20000. Найти вероятность того, что в ближайший день расход электроэнергии в населенном пункте будет от 1500 до 2500 кВт/ч

216. Месячная прибыль компании Мобильные телефоны Средиземья (МТС) является нормальной случайной величиной с математическим ожиданием 1 000 в валюте Средиземья и дисперсией 250 000. Чему равна вероятность того, что прибыль компании окажется: а) в пределах от 500 до 2 000?; б) более 1 250?
Построить график плотности данного нормального распределения и указать на графике область, соответствующую вероятности из пункта а)

218. Имеется случайная величина X, распределенная по нормальному закону, математическое ожидание которой равно 20, среднее квадратичное отклонение равно 3. Найти симметричный относительно математического ожидания интервал, в который с вероятностью р — 0,9972 попадет случайная величина.

219. Случайная величинах распределена по нормальному закону с математическим ожиданием, равным 15, и средним квадратичным отклонением, равным 2. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,954 попадет случайная величина.

220. Известно, что средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратичное отклонение расхода равно 5 кг. Считая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадает с вероятносгью 0,98.

221. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 50 у.е., и стандартным отклонением, равным 6. Определите вероятность того, что в случайно выбранный день обсуждаемого периода цена за акцию была: а) более 60 у.е.; б) ниже 60 за акцию; в) выше 40 за акцию; г) между 42 и 54 у.е. за акцию.

222. Текущая цена акции может быть приближена нормальным распределением с математическим ожиданием 15,28 руб. и средним квадратичным отклонением 0,12 руб. Рассчитать вероятности того, что цена акции окажется:

1) не ниже 15,50 руб.;

2) не выше 15,00 руб.;

3) между 15,10 руб. и 15,40 руб.;

4) между 15,05 руб. и 15,10 руб.

223. Имеется инвестиционный портфель, который стоит из трех видов ценных бумаг. Доли вложения капитала в эти ценные бумаги относятся как , причем . Известно, что нормы прибыли по каждому виду ценных бумаг есть нормально распределенные случайные величины, причем их можно считать независимыми. Средние нормы прибыли по каждому виду ценных бумаг таковы (в процентах): 10, 8, 12; их абсолютные уровни риска (средние квадратические отклонения) таковы (процентах): 3, 1, 4. Найти среднюю норму прибыли всего портфеля и его уровень риска. Найти вероятность того, что норма прибыли по всему портфелю окажется более 12%.

Источник

5.4. Мода и медиана случайной величины

Наряду с математическим ожиданием, дисперсией и моментами для описания распределения случайной величины применяют также моду и медиану.

Модой Mo случайной величины X называется наиболее вероятное значение случайной величины.

Термин «наиболее вероятное значение», строго говоря, применим только к ДСВ, в случае НСВ мода совпадает с таким значением случайной величины, при котором плотность распределения имеет максимум. Различают унимодальные (имеющие одну моду), бимодальные (имеющие две моды) и мультимодальные (имеющие несколько мод) распределения. Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называются антимодальными.

Мода, например, часто используется при экономических расчетах, когда нужно дать ответ на вопрос, каковы преобладающие в данный момент уровни производительности труда, себестоимость, какой товар имеет наибольший спрос и т.д. В связи с этим вводятся понятия модальная производительность, модальная себестоимость и т.д.

Медианой Me случайной величины X называется такое ее значение, для которой справедливо равенство

т.е. равновероятно, что случайная величина окажется меньше или больше медианы.

С геометрической точки зрения, медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Так как вся площадь должна равняться единице, то функция распределения в этой точке равна 0,5:

.

Отметим оптимальное свойство медианы: сумма абсолютных величин отклонений возможных значений случайной величины от медианы, умноженных на соответствующие вероятности, меньше, чем от любой другой величин, т.е. медианы удовлетворяют условию:

Это свойство медианы, в частности, используется в теории оптимального проектирования. Например, при проектировании остановок, при условии, чтобы общий путь пассажиров был минимальным.

Следует отметить, что если распределение симметрично и унимодально, то математическое ожидание, медиана и мода совпадают.

Кроме моды и медианы иногда используются и другие числовые характеристики. Например,

—квантилью Q_ (0 2 максимальную энтропию 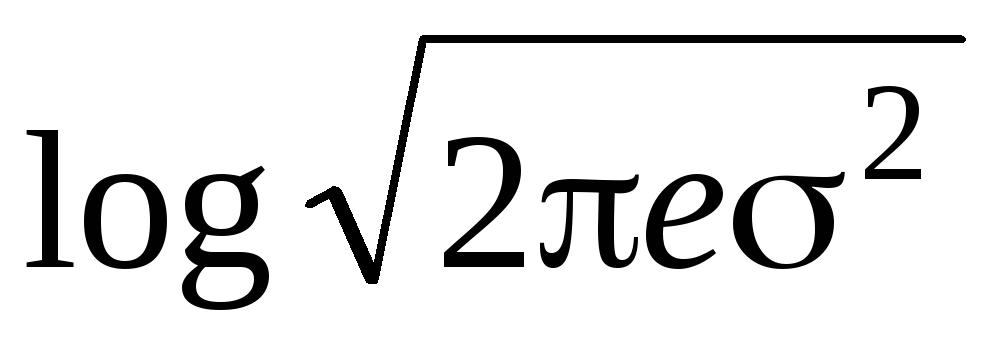имеет нормально распределенная случайная величина.

Источник

Дискретная случайная величина: примеры решений задач

На этой странице мы собрали примеры решения учебных задач о дискретных случайных величинах. Это довольно обширный раздел: изучаются разные законы распределения (биномиальный, геометрический, гипергеометрический, Пуассона и другие), свойства и числовые характеристики, для каждого ряда распределения можно строить графические представления: полигон (многоугольник) вероятностей, функцию распределения.

Ниже вы найдете примеры решений о дискретных случайных величинах, в которых требуется применить знания из предыдущих разделов теории вероятностей для составления закона распределения, а затем вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение, построить функцию распределения, дать ответы на вопросы о ДСВ и т.п.

Примеры для популярных законов распределения вероятностей:

Калькуляторы на характеристики ДСВ

Решенные задачи о ДСВ

Распределения, близкие к геометрическому

Задача 1. На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?

Задача 2. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.

Задачи с независимыми событиями

Задача 6. Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и С.К.О. этой случайной величины. Построить график функции распределения.

Другие задачи и законы распределения ДСВ

Задача 11. Бросают 4 игральные кости. Найти математическое ожидание суммы числа очков, которые выпадут на всех гранях.

Задача 12. Двое поочередно бросают монету до первого появления герба. Игрок, у которого выпал герб, получает от другого игрока 1 рубль. Найти математическое ожидание выигрыша каждого игрока.

Решебник по терверу

Нужны еще решения? Найди в решебнике свое (от 30 рублей и мгновенная доставка):

Источник