все дети любят мороженое а петров не любит значит петровне ребенок
Все млекопитающие дышат легкими. (А1) Кит – млекопитащее. (А2)



Из этого следует, что и кит дышит легкими. (Т)
Различают два основных метода ведения косвенного доказательства: рассуждение от противного и рассуждение по случаям. Оба они основываются на более общем рассуждении методом сведения к противоречию.
Схему рассуждения по случаям можно пояснить на следующем примере. Предположим, что в ситуации принятия делового решения возникла альтернатива, допускающая несколько возможностей действия. В процессе анализа каждого из альтернативных случаев в отдельности отбрасываются те возможные решения, следствия из которых противоречат, скажем, интересам предпринимателя или, может быть, допустим, срокам реализации задач дела. Таким образом, выбирается наиболее приемлемое решение проблемы. Другой пример. Непременным атрибутом следственной практики является выработка спектра альтернативных версий, по-разному объясняющих имеющиеся по делу факты, свидетельские показания и обстоятельства. После проверки и отбрасывания несостоятельных версий доказывается версия, соответствующая собранным доказательствам.
Например: Т – ТЕЗИС АТ – АНТИТЕЗИС
Квадрат – не является кругом. (Т)
Допустим, квадрат является кругом. (АТ)
Если бы квадрат был кругом, у него не было бы углов. Но у него есть углы. Значит, квадрат не является кругом.
ПРОЧИТАЙТЕ ТЕКСТ. КАКИЕ ЯЗЫКОВЫЕ СРЕДСТВА ПОМОГАЮТ ПОНЯТЬ, ЧТО ТЕКСТ НАПИСАН ПОЧТИ 100 ЛЕТ НАЗАД? МЕШАЕТ ЛИ ЭТО ПОНЯТЬ ЕГО СУТЬ? ПРЕДСТАВЬТЕ ИНФОРМАЦИЮ ТЕКСТА В ВИДЕ СХЕМЫ.
Во многих книгах мы встречаем доказательства тех или иных мыслей. Нужно уметь разобраться в них, что не всегда легко, а нередко и очень нелегко. В каждом доказательстве есть три части: 1) тезис — та мысль, которая доказывается; 2) основания, которые приводятся в поддержку тезиса (аргументы) и 3) связь между основаниями и тезисом (способ доказательства, демонстрация),— такая связь, что, приняв основания, мы должны принять тезис: он из них необходимо вытекает. Если основания неприемлемы для нас, то и доказательство неубедительно. Если основания истинны, да тезис из них «не следует», «не вытекает» — тем более неубедительно тогда доказательство автора. Понять доказательство — значит отчетливо выяснить, что доказывается (тезис), какие именно приводятся основания и как вытекает из них тезис. Критиковать доказательство — значит доказывать неприемлемость оснований или отсутствие связи их с тезисом: тезис из них не вытекает и, следовательно, не доказан. Более подробные сведения о доказательствах можно получить из учебников логики. Рисунки и чертежи. Рисунки и чертежи очень важны для понимания многих книг. Чертежи внимательно рассматривает большинство читателей. К сожалению, этого нельзя сказать о рисунках. Тут часто довольствуются общим впечатлением. Например, многие ли из читателей-неспециалистов рассматривали как следует в учебнике зоологии рисунки животных? Вникали во все подробности изображения? Рисунок — суррогат действительности; рассматривание его — суррогат наблюдения. Кто не умеет наблюдать хорошо в действительности, тот не умеет хорошо «наблюдать» и на рисунке; и наоборот, кто учится «наблюдать» на рисунке, тот в большей или меньшей мере улучшает свое уменье наблюдать в действительности. Читая, нужно не упускать из виду этого средства саморазвития.
В ПРИВЕДЕННЫХ НИЖЕ АРГУМЕНТАХ И ЕЗИСАХ ДОПУЩЕНЫ ОШИБКИ. НАЙДИТЕ ОШИБКИ И ЗАПИШИТЕ ИХ. ПОПРОБУЙТЕ ДОКАЗАТЬ ТЕЗИСЫ.
Все дети любят мороженое, а Петров – не любит. Значит, Петров не ребенок.
Мы видим движение Солнца по небосводу и не ощущаем движения Земли, значит Солнце вращается вокруг Земли.
Методические указания к решению задач (стр. 9 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 |
г) Обоснование правдоподобно.
Теория к задаче 40. Опровержением называется логическая операция установления ложности или необоснованности положения, выдвинутого в качестве тезиса. Поскольку доказательство состоит из 3 элементов, то и опровержение может быть трех видов: опровержение тезиса, опровержение аргументов и опровержение демонстрации.
Опровержение тезиса – это операция, цель которой показать несостоятельность тезиса. Опровержение тезиса может быть прямым и косвенным.
Схема прямого опровержения:
1. Условно допускается истинность положения, выдвинутого в качестве тезиса (Т).
2. Из тезиса выводятся следствия. (Приводим к абсурду).
3. Следствия сопоставляются с фактами. Делается вывод о ложности следствий.
4. Из ложности следствий выводится ложность тезиса.
Схема косвенного опровержения:
1. Сразу же выдвигается антитезис (собственная точка зрения).
2. Доказывается антитезис (доказательство прямое).
3. Из истинности антитезиса выводится ложность тезиса.
Задача 40: Построить прямое и косвенное опровержение тезисов.
Пример: Опровергнуть тезис: «Всякий человек может работать юристом в суде».
1. Допустим, что всякий человек может быть юристом в суде.
2. Значит, юристом в суде мог бы быть и ребенок, и ранее судимые лица.
3. Но дети и ранее судимые лица работать юристами в судах не могут.
4. Значит, не всякий человек может работать юристом в суде.
Косвенное опровержение: __
1. Сразу выдвигаем антитезис Т (противоречащее суждение по логическому квадрату): «Некоторые люди не могут работать юристами в судах».
Опровержение тезиса прямым и косвенным методом завершено.
Опровержение аргументов состоит в показе ложности или необоснованности доводов, приводимых противником для доказательства своего тезиса. / Т: «Смит – щедрый человек, потому что он заплатил за всех в ресторане». Вы нападаете на аргумент и показываете его несостоятельность: «Он заплатил не из своего кармана, а эти расходы оплачены его спонсором»/. Следует, правда, помнить, что разоблачение ошибки в аргументации, хотя и разрушает доказательство, но отнюдь еще не свидетельствует о ложности выдвинутого тезиса. Когда же опровержение аргументации выдают за опровержение тезиса, то совершают ошибку «подмены тезиса»: опровергнув одно, выдают это за опровержение другого.
Опровержение демонстрации заключается в показе того, что тезис не следует из приведенных аргументов, что в выводе допущена логическая ошибка. /«Все дети любят мороженное, а Петров – не ребенок. Поэтому, Петров не любит мороженное». Стандартная форма данного умозаключения – первая фигура простого категорического силлогизма. Нарушены правила первой фигуры и правила терминов простого категорического силлогизма. К тому же посылка что все дети любят мороженное – спорный (произвольный) аргумент/.
Задача 41: Составьте тезис на предложенную тему и его обоснование (до 6-7 предложений).
Теория: При выполнении этого задачи следует учитывать правила аргументации:
Правила, касающиеся тезиса:
3. Тезис должен оставаться неизменным на протяжении всего доказательства. Ошибка называется «подменой тезиса». Например, некто выдвигает тезис: «Все население некоего села поддерживает кандидатуру некоего кандидата в депутаты». И приводит аргументы, что «все опрошенные аграрии и пенсионеры собираются за него голосовать». Тем самым, он доказывает не исходный тезис, а более слабый: «Некоторые жители села поддерживают данного кандидата».
4. В тезисе не должно быть логического противоречия. /«Когда я утром вышел из дома, был уже вечер»/.
Правила, касающиеся аргументов:
1. Аргументы должны быть истинными. При нарушении этого правила возникают ошибки необоснованности аргументов: а) «ложный аргумент», когда аргументатор не знает о ложности аргумента; б) «лживый аргумент», когда аргументатор знает о лживости аргумента /«Через сто дней после начала наших реформ в России наступит социально-экономическое процветание»; «Это лекарственное средство поможет от всех болезней», «А знаете ли вы, что 9 из 10 фармацевтов сами принимают Стрепсилс»/; в) «произвольный аргумент», когда аргумент может быть и не ложен, но сам требует должного доказательства /«скоро будет конец мира»/; г) «необоснованная ссылка на авторитет», когда ссылаются на мнение неспециалиста в данной области; когда подобные ссылки применяют не в качестве косвенных доводов, а вместо прямых; когда некие слова «выдергиваются из контекста».
2. Истинность аргумента должна быть доказана независимо от тезиса.
3. Аргументы должны быть релевантными (от англ. relevant – относящимися к делу) по отношению к тезису.
4. Аргументов должно быть достаточно для доказательства тезиса.
Правило, касающиеся демонстрации:
1. В случае доказательства тезис должен логически следовать из аргументов. В случае подтверждения аргументы должны подтверждать тезис, то есть повышать степень вероятности его истинности. Когда в доказательстве тезис не следует из аргументов, то возникает ошибка «не следует». Примеры ошибки «не следует»: а) «Хлеб у нас подорожает, потому что в Америке было землетрясение»; б) «Н. – добрый и порядочный человек, поэтому он не причастен к преступлению».
Хотя правила сами по себе довольно просты, но их формулировка важна для того, чтобы предупредить некоторые типичные ошибки логического характера.
Методические указания составлены доцентами и для решения задач по учебному пособию «Логика: сборник задач». Улан-Удэ, изд-во ВСТГУ, 2004.
[1] Поскольку ПКС строится из простых категорических суждений, прежде всего, необходимо вспомнить теоретический материал к теме «Простые суждения».
[2] Распределенность терминов см. в теории к задаче 16.
[3] Определения различных видов простых суждений указаны в теории к задачам 14-18.
[4] Определение логического закона дано в теории к задачам 20, 21.
[5] Необходимая теоретическая информация по дедукции и индукции описана в предыдущем задании.
Тема 12. Основы теории аргументации
Теория к задачам 39-41: Аргументация – это операция обоснования каких-либо суждений, практических решений или оценок, в которой наряду с логическими приемами применяются также внелогические методы и приемы убеждающего воздействия. Обоснование может быть полным и неполным. При полном обосновании (доказательстве) тезис непосредственно следует из аргументов. Неполное обоснование называется подтверждением.
Доказательство – логическая операция полного обоснования истинности какого-либо положения с помощью других положений, истинность которых уже установлена. В структуру доказательства входят три элемента: 1) Тезис Т – доказываемое положение. 2) Аргументы – вспомогательные положения, с помощью которых обосновывается тезис. 3) Демонстрация – логическая связь между аргументами и тезисов. В качестве аргументов используются: 1) установленные общие положения (различного рода принципы, нормы права, законы, общие правовые, уставные положения и т.д.). 2) удостоверенные суждения о фактах (данные наблюдений, экспериментов, экспертиз, документы; статистические обобщения и т.д.) 3) суждения, принимаемые в качестве очевидных (аксиомы; постулаты; определения; высказывания, многократно проверенные практикой).
Доказательство может быть прямым и косвенным. При прямом доказательстве подбираются аргументы, прямо направленные на доказательство тезиса. При косвенном доказательстве используют антитезис – суждение, противоречащее тезису.
Схема прямого доказательства:
1. Подбираются аргументы, прямо направленные на обоснование тезиса (по дедукции, по индукции или аналогии).
Схема косвенного апагогического («от противного») доказательства.
1. Выдвигается антитезис.
2. Из антитезиса выводятся следствия.
3. Следствия сопоставляются с фактами.
4. Из ложности следствий выводится ложность антитезиса. А отсюда – истинность тезиса.
Задача 39: Постройте прямое и косвенное доказательство тезиса, используя в качестве демонстрации дедукцию, а затем индукцию
Пример 1: Доказать тезис: Все студенты группы 555 – успевающие студенты.
А) Прямое дедуктивное доказательство:
Студенты, вовремя и успешно сдающие экзамены, являются успевающими студентами. Все студенты группы 555 вовремя и успешно сдают экзамены. Значит, действительно, все студенты группы 555 – успевающие студенты.
Здесь в качестве демонстрации применялся простой категорический силлогизм, построенный по первой фигуре:
Правила ПКС соблюдены. Значит, умозаключение построено правильно. Тезис доказан.
Б) Прямое доказательство по индукции:
Студент А – успевающий студент.
Студент Б – успевающий студент.
Студент Я – успевающий студент.
Значит, все студенты 555 группы – успевающие студенты.
В) Косвенное апагогическое доказательство:
1. Условно выдвигаем антитезис: Если бы не все студенты группы 555 были успевающими.
2. Выводим следствия. Тогда бы среди них были задолжники по сессии.
3. Опровергаем следствия. Но среди них нет задолжников по сессии.
4. Значит, наше допущение «не все студенты группы 555 – успевающие студенты» ложно. Следовательно, истинно, что все студенты группы 555 – успевающие студенты.
Теория к задаче 40. Опровержением называется логическая операция установления ложности или необоснованности положения, выдвинутого в качестве тезиса. Поскольку доказательство состоит из 3 элементов, то и опровержение может быть трех видов: опровержение тезиса, опровержение аргументов и опровержение демонстрации.
Опровержение тезиса – это операция, цель которой показать несостоятельность тезиса. Опровержение тезиса может быть прямым и косвенным.
Схема прямого опровержения:
1. Условно допускается истинность положения, выдвинутого в качестве тезиса (Т).
2. Из тезиса выводятся следствия. (Приводим к абсурду).
3. Следствия сопоставляются с фактами. Делается вывод о ложности следствий.
4. Из ложности следствий выводится ложность тезиса.
Схема косвенного опровержения:
1. Сразу же выдвигается антитезис (собственная точка зрения).
2. Доказывается антитезис (доказательство прямое).
3. Из истинности антитезиса выводится ложность тезиса.
Задача 40: Построить прямое и косвенное опровержение тезисов.
Пример: Опровергнуть тезис: «Всякий человек может работать юристом в суде».
1. Допустим, что всякий человек может быть юристом в суде.
2. Значит, юристом в суде мог бы быть и ребенок, и ранее судимые лица.
3. Но дети и ранее судимые лица работать юристами в судах не могут.
4. Значит, не всякий человек может работать юристом в суде.
Косвенное опровержение: __
1. Сразу выдвигаем антитезис Т (противоречащее суждение по логическому квадрату): «Некоторые люди не могут работать юристами в судах».
Опровержение тезиса прямым и косвенным методом завершено.
Опровержение аргументов состоит в показе ложности или необоснованности доводов, приводимых противником для доказательства своего тезиса. / Т: «Смит – щедрый человек, потому что он заплатил за всех в ресторане». Вы нападаете на аргумент и показываете его несостоятельность: «Он заплатил не из своего кармана, а эти расходы оплачены его спонсором»/. Следует, правда, помнить, что разоблачение ошибки в аргументации, хотя и разрушает доказательство, но отнюдь еще не свидетельствует о ложности выдвинутого тезиса. Когда же опровержение аргументации выдают за опровержение тезиса, то совершают ошибку «подмены тезиса»: опровергнув одно, выдают это за опровержение другого.
Опровержение демонстрации заключается в показе того, что тезис не следует из приведенных аргументов, что в выводе допущена логическая ошибка. /«Все дети любят мороженное, а Петров – не ребенок. Поэтому, Петров не любит мороженное». Стандартная форма данного умозаключения – первая фигура простого категорического силлогизма. Нарушены правила первой фигуры и правила терминов простого категорического силлогизма. К тому же посылка что все дети любят мороженное – спорный (произвольный) аргумент/.
Задача 41: Составьте тезис на предложенную тему и его обоснование (до 6-7 предложений).
Теория: При выполнении этого задачи следует учитывать правила аргументации:
Правила, касающиеся тезиса:
3. Тезис должен оставаться неизменным на протяжении всего доказательства. Ошибка называется «подменой тезиса». Например, некто выдвигает тезис: «Все население некоего села поддерживает кандидатуру некоего кандидата в депутаты». И приводит аргументы, что «все опрошенные аграрии и пенсионеры собираются за него голосовать». Тем самым, он доказывает не исходный тезис, а более слабый: «Некоторые жители села поддерживают данного кандидата».
4. В тезисе не должно быть логического противоречия. /«Когда я утром вышел из дома, был уже вечер»/.
Правила, касающиеся аргументов:
1. Аргументы должны быть истинными. При нарушении этого правила возникают ошибки необоснованности аргументов: а) «ложный аргумент», когда аргументатор не знает о ложности аргумента; б) «лживый аргумент», когда аргументатор знает о лживости аргумента /«Через сто дней после начала наших реформ в России наступит социально-экономическое процветание»; «Это лекарственное средство поможет от всех болезней», «А знаете ли вы, что 9 из 10 фармацевтов сами принимают Стрепсилс»/; в) «произвольный аргумент», когда аргумент может быть и не ложен, но сам требует должного доказательства /«скоро будет конец мира»/; г) «необоснованная ссылка на авторитет», когда ссылаются на мнение неспециалиста в данной области; когда подобные ссылки применяют не в качестве косвенных доводов, а вместо прямых; когда некие слова «выдергиваются из контекста».
2. Истинность аргумента должна быть доказана независимо от тезиса.
3. Аргументы должны быть релевантными (от англ. relevant – относящимися к делу) по отношению к тезису.
4. Аргументов должно быть достаточно для доказательства тезиса.
Правило, касающиеся демонстрации:
1. В случае доказательства тезис должен логически следовать из аргументов. В случае подтверждения аргументы должны подтверждать тезис, то есть повышать степень вероятности его истинности. Когда в доказательстве тезис не следует из аргументов, то возникает ошибка «не следует». Примеры ошибки «не следует»: а) «Хлеб у нас подорожает, потому что в Америке было землетрясение»; б) «Н. – добрый и порядочный человек, поэтому он не причастен к преступлению».
Хотя правила сами по себе довольно просты, но их формулировка важна для того, чтобы предупредить некоторые типичные ошибки логического характера.
Методические указания составлены доцентами Гомбоевой Л.В. и Кузьминым А.В. для решения задач по учебному пособию «Логика: сборник задач». Улан-Удэ, изд-во ВСТГУ, 2004.
[1] Поскольку ПКС строится из простых категорических суждений, прежде всего, необходимо вспомнить теоретический материал к теме «Простые суждения».
[2] Распределенность терминов см. в теории к задаче 16.
[3] Определения различных видов простых суждений указаны в теории к задачам 14-18.
[4] Определение логического закона дано в теории к задачам 20, 21.
[5] Необходимая теоретическая информация по дедукции и индукции описана в предыдущем задании.
Да тут и не поспоришь
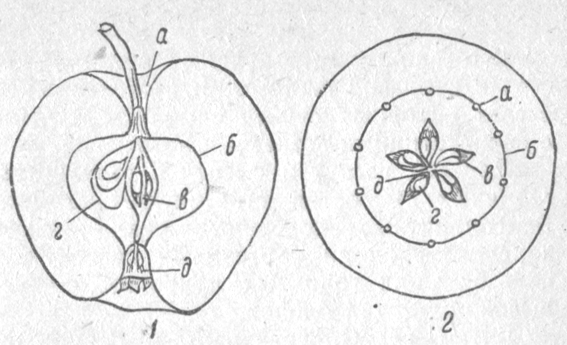
Яблоки в карамели
Бывает, приходит в голову какая-то идея и тебе её срочно нужно воплотить в жизнь. Захотелось приготовить яблоки в карамели, такие, знаете, как в Американских фильмах, где маленькие девочки в парке развлечений едят глянцевые яблоки на палочке и фотографируются с клоунами.
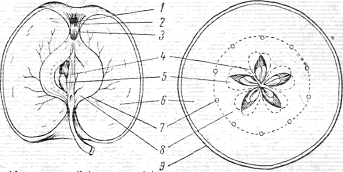
Казалось бы, что могло пойти не так? Находясь на этапе «удалите плодоножку и вот то, что раньше было цветочком и вставьте шпажку», началооось. Я вставила шпажку в то место, где был цветочек: «Ты зачем вставила шпажку в верх? Теперь у тебя яблоки получатся вверх ногами!“ Я говорю, ну как же вверх ногами, когда как раз правильно? И показываю картинку, как пример:
Ну, то есть, когда будешь держать яблоко за палочку, оно как раз будет как положено. Вот ещё пример, на нём яблоки в шоколаде, но не суть.
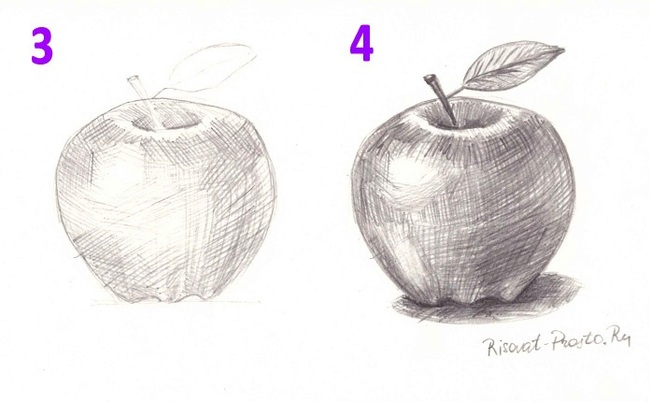
На что мне показали другую картинку, что правильно вставлять палочку в то место, откуда удалили хвостик.
В ответ мне крутили пальцем у виска и тыкали меня носом в картинку из интернета, явно австралийскую:
Я кричала, что даже в букваре яблоко нарисовано так, что хвостик вверху, а значит, это верх!
Лексика переставала быть культурной, мой оппонент негодовал и сокрушался, что логики у меня нет, так как «хвостик» яблока на то и хвостик, хвост! А хвост находится где? Правильно, в жопе! А цветочек, следовательно, это нос! И вообще, сравни яблоко с огурцом, где у него носик и где жопка? То-то же!
Но и у меня аргументы не заканчивались. «Художники!»-кричала я. «Художники тоже по твоему в своих академических рисунках учатся рисовать яблоки вверх ногами?!“- я яростно тыкала пальцем в экран телефона.
Я же судорожно гуглила и тыкала пальцем в новые картинки. «Вот, смотри же! Яблоки разных сортов, уж яблоковеды их не стали бы подписывать вверх ногами! Уж они то знают!»
К вечеру были опрошены все родные и знакомые. Мнения разделились. Спор так и остался открытым. Но я не сдамся и спрошу ещё раз: где у яблока верх, а где низ?!
Все дети любят мороженое а петров не любит значит петровне ребенок
Задачи 2.4–2.10, 2.14, 2.15 связаны с построением отрицания к общим и частным высказываниям. Меньше всего нам бы хотелось, чтобы итогом занятия стала формулировка соответствующей пары правил, которое дети будут потом применять в задачах. А больше всего – чтобы они грамотно строили отрицания, не задумываясь о правилах. Если на этом занятии дети много ошибаются, продолжайте предлагать на последующих занятиях аналогичные упражнения (в том числе из раздела дополнительных задач) до победного конца.
Можно ли одну и ту же мысль выразить по-разному? Насколько сильно зависит смысл русского предложения от порядка слов? Всегда ли одинаково следует понимать одни и те же слова? Не будем пытаться на одном занятии изучить весь русский язык. Ограничимся несколькими словами и выражениями: «все», «каждый (любой)», «некоторые», «существует», «хотя бы один».
Задача 2.1. 1) Серый Волк заинтересовался цветом шапочек. Однажды он встретил Красную Шапочку. Помогите Волку сделать правильный вывод. Придумайте несколько вариантов.
2) Выразите другими словами мысль «Все шапочки красные».
Решение. 1) Можно сказать: «Некоторые шапочки красные». Но можно и по-другому. Например, так:
Шапочки бывают красные.
Иногда встречаются красные шапочки и т. п.
Математики любят говорить точно: «Существует хотя бы одна красная шапочка».
2) «Шапочки всегда красные», «Любая шапочка красная» или «Каждая шапочка красная».
Задача 2.2. Вася говорит, что слова «для всех» и «для каждого» означают одно и то же. Прав ли Вася?
Решение. Вопрос скорее лингвистический, чем математический. Часто смысл предложения действительно не меняется при замене «для всех» на «для каждого» и соответствующих изменениях формы слов. Например, «Для всех принцесс горошины под периной невыносимы» означает то же, что и «Для каждой принцессы горошина под периной невыносима». Но вот если вместо «Выдать зимовщикам для всех одну пару валенок» попросить «Выдать зимовщикам для каждого одну пару валенок», зимовщики наверняка заметят разницу.
Задача 2.3. 1) Означают ли одно и то же высказывания: «Некоторые сантехники любят рэп» и «Некоторые любители рэпа – сантехники»?
2) Означают ли одно и то же высказывания: «Все сантехники любят рэп» и «Все любители рэпа – сантехники»?
Ответ. 1) Да. 2) Нет.
Решение. 1) Чтобы лучше разобраться в смысле высказываний, изобразим их с помощью кругов Эйлера (см. рис. 1). Пусть в одном круге находятся сантехники, в другом – любители рэпа. Если первое высказывание истинно, то круги непременно пересекаются, и в пересечении кругов располагается хотя бы один сантехник, любящий рэп. Но ровно это же требуется и для истинности второго утверждения. Поэтому они означают одно и то же.
2) Снова разместим сантехников и рэперов в пересекающихся кругах. В пересечении кругов, как и прежде, расположены сантехники, любящие рэп. Сантехники, НЕ любящие рэп, окажутся в серой части рисунка 2. Если таковых нет (т. е. все сантехники любят рэп), то серая часть пуста.
Чтобы показать это на рисунке, принято изображать круг сантехников внутри круга рэперов (см. рис. 3).
Сравнение рисунков 3 и 4 помогает понять, почему смысл высказываний «Все сантехники любят рэп» и «Все любители рэпа – сантехники» разный.
Рис. 4. Все любители рэпа – сантехники
Задача 2.5. Рассмотрим два утверждения. Сколько из них могут быть верными?
2) В этой корзине есть хотя бы один ядовитый гриб.