внутри круга взяли произвольную точку а где на окружности нужно взять такую точку б
Экстремальные задачи по геометрии (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
Задача 13. Каково наименьшее число кругов, которыми можно покрыть круг вдвое большего радиуса?
Решение. 7 кругов. Каждый маленький круг может покрыть дугу окружности большого круга, не большую чем 60
Задача 14. На данной прямой c найти точку C, из которой данный отрезок AB виден под наибольшим углом. Точки A и B лежат по одну сторону от прямой c.
Решение. Рассмотрим окружность, проходящую через точки A, B и касающуюся прямой c в точке C. Эта точка C и будет искомой. Действительно, для любой другой точки C’ прямой c угол AC’B измеряется полуразностью дуг AB и A’B’ окружности (рис. 8) и, следовательно, меньше угла ACB.
 |
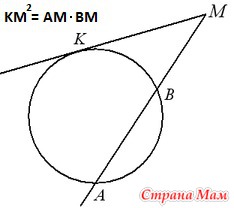
Задача 15. Внутри окружности с центром O дана точка A, отличная от O. Найдите на окружности точку M, для которой угол AMO наибольший.
Решение. Пусть M – произвольная точка окружности, OK – перпендикуляр, опущенный из точки O на прямую MA (рис. 9). В прямоугольном треугольнике KMO гипотенуза OM постоянна (равна радиусу), следовательно, угол AMO тем больше, чем больше катет OK. Поэтому угол OMA будет наибольшим, когда угол OAM – прямой.
В качестве самостоятельной работы предлагаем следующие задачи.
Задача 16. На данной прямой найдите точку, из которой данная окружность видна под наибольшим углом.
Задача 17. На данной окружности найдите точку, из которой данный отрезок виден под наибольшим углом.
Рассмотрим теперь одну из классических экстремальных задач – задачу Герона, имеющую многочисленные приложения
Задача 18. Дана прямая с и две точки А и В, не лежащие на этой прямой. Требуется найти такую точку С на прямой c, чтобы сумма расстояний АС + СВ была наименьшей.
Решение. Рассмотрим сначала случай, когда точки A и B лежат по разные стороны от прямой c (рис. 10,а). Легко видеть, что в этом случае искомой точкой C является точка пересечения отрезка AB и прямой c. Для любой другой точки C’ прямой c будет выполняться неравенство AC + CB C1’C2’. Последнее неравенство выполняется, так как длина ломаной больше длины отрезка, соединяющего ее концы. Следовательно, точки A и B являются искомыми точками,
 |
для которых длина соответствующей ломаной наименьшая.
Задача 24. Внутри угла со сторонами a и b дана точка C. Требуется найти такие точки A и B на сторонах этого угла, чтобы периметр треугольника ABC был наименьшим.
Ясно, что эта задача получается из предыдущей, если положить C1 = C2 = C. Построение соответствующих точек A и B можно предложить учащимся в качестве самостоятельной работы. Решение показано на рисунке 13, в котором точки C’, C” симметричны точке C относительно прямых a, b соответственно.
Рассмотрим вопрос о том, в каком случае существует решение этой и предыдущей задач.
Дело в том, что прямая C’C” может не пересекать стороны угла. Выясним, в каких случаях это может происходить.
Обозначим через O вершину угла и соединим ее отрезками с точками C’, C” и C (рис. 14, а). Тогда 




Одной линейкой
Задача
Даны окружность с центром О и точка А вне окружности. а) Проведен диаметр окружности. Пользуясь только линейкой*, опустите перпендикуляр из точки А на этот диаметр. б) Через точку А проведена прямая, не имеющая общих точек с окружностью. Пользуясь только линейкой, опустите перпендикуляр из точки О на эту прямую.
*Примечание. Под «линейкой» в задачах на построение всегда подразумевается не измерительный инструмент, а геометрический — с его помощью можно только проводить прямые (через две имеющиеся точки), но не измерять расстояние между точками. Кроме того, геометрическая линейка считается односторонней — с ее помощью нельзя провести параллельную прямую, просто приложив одну сторону линейки к двум точкам и проведя линию вдоль другой стороны.
Подсказка 1
Используйте концы диаметра, а не центр окружности.
Подсказка 2
Угол с вершиной на окружности, опирающийся на ее диаметр, — прямой. Зная это, вы можете построить две высоты в треугольнике, образованном концами диаметра и точкой А.
Подсказка 3
Попробуйте решить сначала более простой случай, чем заданный в пункте б), — когда данная прямая пересекает окружность.
Решение
а) Пусть ВС — данный диаметр (рис. 1). Для решения задачи просто вспомним первые две подсказки: если провести прямые AВ и АC, а затем соединить точки их пересечения с окружностью с нужными вершинами треугольника ABC, то получатся две высоты этого треугольника. А так как высоты треугольника пересекаются в одной точке, то прямая CH будет третьей высотой, то есть искомым перпендикуляром из А к диаметру ВС.

б) Решение этого пункта, однако, даже в том случае, который дан в третьей подсказке, не кажется более простым: да, мы можем провести диаметры, соединить их концы и получить прямоугольник ABCD (рис. 2, на котором, для простоты, точка А отмечена на окружности), но как это приближает нас к построению перпендикуляра из центра окружности?
А вот как: так как треугольник AOB равнобедренный, то перпендикуляр (высота) OK пройдет через середину K стороны AB. А значит, задача свелась к нахождению середины этой стороны. Как ни удивительно, но окружность больше нам совсем не нужна, да и точка D тоже, в общем, «лишняя». А вот отрезок CD — не лишний, но на нем нам потребуется не какая-то конкретная точка, а совершенно произвольная точка E! Если обозначить за L точку пересечения BE и AC (рис. 3), а затем продлить AE до пересечения с продолжением BC в точке M, то прямая LM — это решение всех наших забот и проблем!

Правда, очень похоже, что LM пересекает AB посередине? Это и правда так. Попробуйте доказать это. Мы же отложим доказательство до конца решения задачи.
Итак, мы научились находить середину отрезка AB, а значит, научились опускать перпендикуляр на AB из центра окружности. Но что делать с исходной задачей, в которой данная прямая не пересекает окружность, как на рис. 4?
Постараемся свести задачу к уже решенной. Это можно сделать, например, так.
Сначала построим прямую, симметричную данной относительно центра окружности. Построение понятно из рис. 5, на котором данная прямая — горизонтальная под окружностью, а построенная симметричная ей — выделена красным (две синие точки могут быть взяты на окружности совершенно произвольно). Заодно проведем через центр О еще одну прямую, перпендикулярную к одной из сторон получившегося в окружности прямоугольника, чтобы получить на данной прямой два равных по длине отрезка.
Имея две параллельные прямые, на одной из которых уже отмечены два конца и середина отрезка, возьмем произвольную точку T (например, на окружности) и построим такую точку S, что прямая TS будет параллельна имеющимся двум прямым. Это построение показано на рис. 6.
Тем самым мы получили хорду окружности, параллельную данной прямой, то есть свели задачу к решенной ранее версии, ведь к такой хорде проводить перпендикуляр из центра окружности мы уже умеем.
Осталось привести доказательство факта, который мы использовали выше.
Четырехугольник ABCE на рис. 3 — трапеция, L — точка пересечения ее диагоналей, а M — точка пересечения продолжений ее боковых сторон. По известному свойству трапеции (его еще называют замечательным свойством трапеции; здесь можно посмотреть, как оно доказывается) прямая ML проходит через середины оснований трапеции.
Собственно, еще раз мы фактически опирались на эту же теорему уже в последней подзадаче, когда проводили третью параллельную прямую.
Послесловие
Теория геометрических построений одной линейкой, когда задана вспомогательная окружность с центром, разработана замечательным немецким геометром XIX века Якобом Штейнером (правильнее произносить его фамилию Steiner как «Штайнер», но в отечественной литературе уже давно закрепилось написание с двумя «е»). О его математических достижениях мы уже однажды рассказывали в задаче «Короче, Склифосовский». В книге «Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга» Штейнер доказал теорему, согласно которой любое построение, которое может быть выполнено с помощью циркуля и линейки, может быть выполнено и без циркуля, если задана всего одна окружность и отмечен ее центр. Доказательство Штейнера сводится к демонстрации возможности осуществления базовых построений, обычно выполняемых с помощью циркуля, — в частности, к проведению параллельных и перпендикулярных прямых. Наша задача, как легко видеть, является частным случаем этой демонстрации.
Впрочем, к некоторым задачам Штейнер привел не единственный способ решения. Приведем второй способ и мы.
Возьмем на данной прямой две произвольные точки A и B (рис. 7). Сначала строим перпендикуляр из A на (синюю) прямую BO — это фактически решение нашей первой задачи, потому что эта прямая содержит диаметр окружности; все соответствующие построения на рис. 7 выполнены синим цветом. Затем строим перпендикуляр из B на (зеленую) прямую AO — это точно такое же решение точно такой же задачи, построения выполнены зеленым цветом. Тем самым мы получили две высоты треугольника AOB. Третья высота этого треугольника проходит через центр O и точку пересечения двух других высот. Она и является искомым перпендикуляром к прямой AB.
Но и это еще не все. Несмотря на всю (относительную) простоту второго способа, он «избыточно длинный». Это означает, что существует другой способ построения, требующий меньшего числа операций (в задачах на построение каждая линия, проведенная циркулем или линейкой, считается как одна операция). Построения, требующие минимального среди известных количества операций, французский математик Эмиль Лемуан (Émile Lemoine, 1840–1912) назвал геометрографическими (см.: Geometrography).
Итак, вашему вниманию предлагается геометрографическое решение пункта б). Оно требует всего 10 шагов, при этом шесть первых — «естественные», а следующие три — «удивительные». Самый последний шаг, проведение перпендикуляра, пожалуй, тоже следует назвать естественным.
Мы хотим провести красный пунктирный перпендикуляр (рис. 8), для этого нам нужно отыскать на нем какую-нибудь точку, отличную от О. Поехали.
1) Пусть A — произвольная точка на прямой, а C — произвольная точка на окружности. Проводим прямую AC.
2)–3) Проводим диаметр OC (вторично пересекающий окружность в точке D) и прямую AD. Отмечаем вторые точки пересечения прямых AC и AD с окружностью — B и E, соответственно.
4)–6) Проводим BE, BD и CE. Прямые CD и BE пересеклись в точке H, а BD и CE — в точке G (рис. 9).
Кстати, а могло ли случиться так, что BE оказалось бы параллельно CD? Да, безусловно. В случае, когда диаметр CD перпендикулярен AO, то именно так и случается: BE и CD параллельны, а точки A, O и G лежат на одной прямой. Но возможность брать точку C произвольно предполагает наше умение выбрать ее так, чтобы CO и AO не были перпендикулярны!
И вот теперь обещанные удивительные шаги построения:
7) Проводим GH до пересечения с данной прямой в точке I.
8) Проводим CI до пересечения с окружностью в точке J.
9) Проводим BJ, которая пересекается с GH. где? Правильно, в красной точке, которая находится на вертикальном диаметре окружности (рис. 10).
10) Проводим вертикальный диаметр.
Вместо шага 8 можно было бы провести прямую DI, а затем на шаге 9 соединить вторую точку ее пересечения с окружностью с точкой E. Результат был бы той же самой красной точкой. Правда, это удивительно? Причем, даже неясно, что удивляет сильнее — то, что красная точка оказывается одной и той же для двух способов построения, или то, что она лежит на искомом перпендикуляре. Впрочем, геометрия — это ведь не «искусство факта», а «искусство доказательства». Так что постарайтесь доказать это.
Мелкая придирка не по существу:
> правильнее произносить его фамилию Steiner как «Штайнер», но в
> отечественной литературе уже давно закрепилось написание с двумя «е»
А по существу вопрос: теорема гласит, что «любое построение, которое может быть выполнено с помощью циркуля и линейки, может быть выполнено и без циркуля, если задана всего одна окружность и отмечен ее центр».
Что имеется в виду под «если задана всего одна окружность»? Имеется ли в виду, что в задаче дана только одна окружность, и задание центра позволяет построить линейкой все то, что можно построить циркулем? Или имеется в виду, что берем любую задачу (скажем, деление отрезка пополам), и достаточно где-нибудь в произвольном месте задать окружность и ее центр, чтобы задача деления отрезка пополам решалась одной линейкой?
Да, имеется в виду ровно это. На плоскости чертежа задана произвольная окружность и ее центр. Это позволяет выполнить одной линейкой всё, что можно сделать циркулем и линейкой.
> А деление отрезка пополам и так решается одной линейкой (без вспомогательной окружности
Допускаю, хотя не знаю такого способа.
Этого не может быть. По теореме Мора-Маскерони.
Этого противоречит вашим словам, будто линейкой можно построить середину отрезка.
Вот смотрите: если мы можем одной линейкой построить касательную к окружности из точки A, значит, возьмем две такие касательные. Проведем хорду, опирающуюся на две точки касания.
По вашим словам (выше), одной линейкой можно найти середину отрезка, а значит, и этой хорды.
Из исходной точки A через середину хорды проведем прямую. Это будет (продолженный) диаметр окружности.
Возьмем произвольную точку B и повторим с ней и той же окружностью то же самое. Получим второй диаметр.
Два диаметра дают нам центр окружности.
Итого получается, что если, как вы утверждаете, одной линейкой можно построить и касательную из заданной точки к заданной окружности, и середину заданного отрезка, то одной линейкой можно построить и центр данной окружности. Однако хорошо известно (доказано, по-моему, тем же Штейнером через сечения наклонного конуса), что это невозможно. А если б было возможно, то рассказанная вами теорема Штейнера-Понселе не имела бы смысла: получается, любое построение циркулем и линейкой можно было бы совершить просто линейкой безо всяких дополнительных условий (или точнее, требовалось бы иметь где-то окружность не обязательно с отмеченным центром).
Касательную одной линейкой точно можно построить, и это ничему не противоречит.
Что касается утверждения о построении середины отрезка, я хотел сказать вот что: для этого не нужно иметь вспомогательную окружность, достаточно иметь вспомогательную параллельную прямую.
Да, это тоже исследовано Штейнером. Он рассмотрел списки задач, разрешимых линейкой при следующих дополнительных условиях
а) дана одна параллельная прямая или отрезок, разделенный в известном рациональном отношении
б) даны две пары параллельных прямых, или два отрезка, деленные в рац. отношениях, или одна пара параллельных и один такой отрезок
в) дан вспомогательный квадрат
Все эти условия позволяют решать линейкой какой-то класс задач на построение, причем а) Ответить
Тогда и задача немного другая, и решение другое. Фактически в вашей задаче требуется построить квадрат по заданным противоположным вершинам (B и C).
Всё про окружность и круг
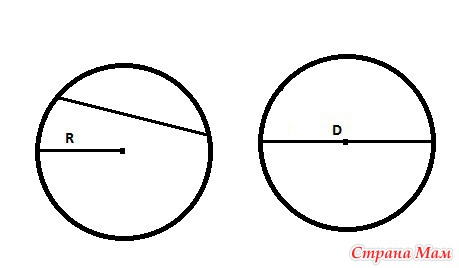
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
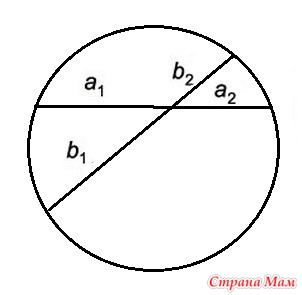
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
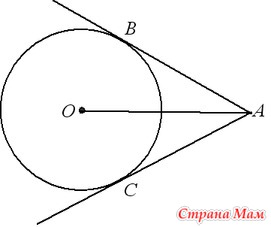
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
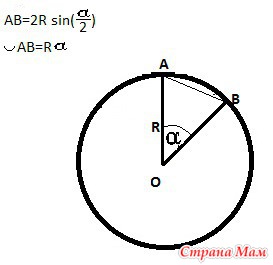
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
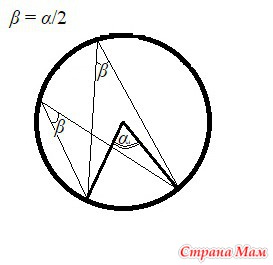
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
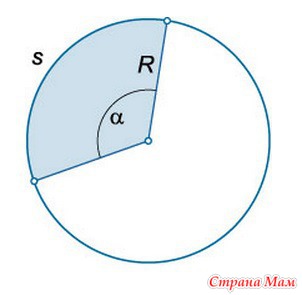
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Теорема 1. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть есть величина постоянная
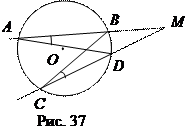


Δ СВМ (Ð А = Ð С – как вписанные углы, опирающиеся на одну и туже дугу ВD, Ð М – общий), то 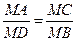


Следствие 1. Произведение секущей, проведённой через точку М, находящуюся на расстоянии а от центра круга
радиуса R, а > R, на её внешнюю часть равна а 2 – R 2 .
Действительно, по теореме 1:
МА 

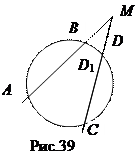


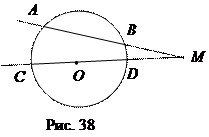
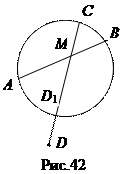
Доказательство. Пусть через точки А, В, С проведена окружность и D1 – её вторая точка пересечения с прямой МС. Тогда по теореме 1: МА 






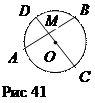
Доказательство.Пусть через точку М внутри круга с центром О произвольно проведены две хорды АВ и СD. Докажем, что МА 

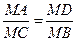


Теорема 4. Если отрезки АВ и СD пересекаются в точке М и МА 







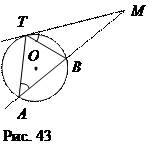
Теорема 5. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть равно квадрату касательной (рис. 43).

Задача 1. В круг поместили замкнутую ломанную из пяти звеньев одинаковой длинны. Каждое звено ломаной продолжили до пересечения с окружностью отрезками зелёного и синего цвета, причём из одной вершины ломаной выходят отрезки разного цвета. Доказать, что сумма длин зелёных отрезков совпадает с суммой длин синих.
7.2.Из теорем 1 и 3 следует, что величина a 2 – R 2 является характеристикой взаимного расположения круга и точки из плоскости круга, где а – расстояние от точки до центра круга, R – радиус круга. Величину a 2 – R 2 называют степенью точки по отношению к кругу.
Теорема 7. ГМТ, которые имеют одну и ту же степень в отношении двух кругов, есть перпендикуляр к линии их центров.

По следствию 4.3 точка М принадлежит определённому перпендикуляру к прямой ОО1. Пусть N –произвольная точка перпендикуляра к прямой ОО1, который определён условием ОМ 2 – O1M 2 = R 2 – R1 2 .
Последнее равенство означает, что точка N имеет одинаковые степени по отношению к двум кругам. Доказательство остаётся в силе, если, например, R1 = 0.
Следствие 3. ГМТ, степени которых по отношению к заданной точке равны, есть перпендикуляр к прямой, которая проходит через эту точку и центр окружности.
ГМТ, о которых идёт речь в теореме 7 и следствии 3, называются радикальной осью двух кругов и радикальной осью круга и точки соответственно.
Следствие 4. Два концентрических круга не имеют радикальной оси.
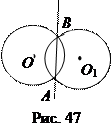
Действительно, степени точек А и В (рис. 47) по отношению к каждому из кругов О и О1 равны нулю.
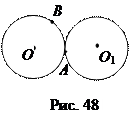
Действительно, если бы радикальная ось имела с окружностью О одну, кроме А, общую точку В (рис. 48), то эта точка должна была иметь степень О и в отношении к кругу О1. Поэтому она принадлежала бы и окружности О1. Но окружности не имеют других общих точек, кроме А. Поэтому радикальная ось является касательной к окружности О, и значит, к кругу О1.
Следствие 7. Радикальные оси любых двух из трёх окружностей или параллельны, или пересекаются в одной точке.
Действительно, если какие-нибудь две из трёх радикальных осей имеют общую точку, то через неё пройдёт и третья радикальная ось.