в материалах международного конкурса по информатике бобер есть такая задача предложенная
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
В Международном конкурсе по информатике «Бобёр» школьникам была предложена задача «Склад», подготовленная специалистами из Японии.
13. В Международном конкурсе по информатике «Бобёр» школьникам была предложена задача «Склад», подготовленная специалистами из Японии. Вот её условие.
Плотник в Бобровой Деревне использует 31 склад, пронумерованный от 1 до 31. Однажды он забыл, сколько складов уже заполнил, но помнит, что заполнял их в порядке возрастания номеров.
Чтобы уменьшить количество открывания дверей, он действует следующим образом:
Сначала открывает склад со средним номером — склад № 16. Затем:
• если склад № 16 пуст, он решает искать первый незаполненный склад в промежутке от № 1 до № 15, открывает опять средний склад — склад № 8 — и повторяет процедуру;
• если склад № 16 заполнен, то нужный склад он ищет между № 17 и № 31, открывает средний склад — склад № 24 — и повторяет процедуру.
После всех действий плотник обнаружил, что заполнены были склады от № 1 до № 15 включительно. Сколько дверей ему пришлось открыть?
Решите эту задачу. Какой из рассмотренных нами методов поиска был использован героем этой задачи?
Ответ
Двоичный поиск эффективно определяет положение искомого элемента (или его отсутствие) в упорядоченном наборе. Это один из базовых и важных алгоритмов.
Если склады от №1 до №15 заполнены, то: — когда плотник открывает склад №16, он оказывается пуст (1-ая открытая дверь);
— тогда плотник решает искать между №1 и №15, открывает склад №8, он оказывается заполнен (2-ая открытая дверь);
— теперь он ищет между №9 и №15, открывает склад №12 — он заполнен (3-ья открытая дверь);
— далее он ищет между №13 и №15, открывает склад №14 — он заполнен (4-ая открытая дверь);
— наконец он открывает последний склад № 15 (5-ая дверь).
ГДЗ по информатике 11 класс учебник Босова параграф 11
1. В решении каких прикладных задач используются алгоритмы нахождения кратчайшего пути между заданными вершинами в графе?
С их помощью можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
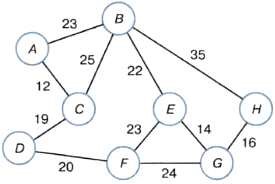
2. С помощью алгоритма Дейкстры найдите кратчайший путь между вершинами А и G следующего графа:
В материалах международного конкурса по информатике «Бобёр» есть такая задача, предложенная разработчиками из Нидерландов.
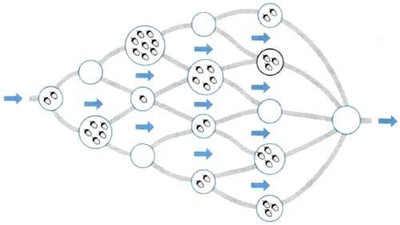
Бобёр Билли любит жёлуди. Он хочет поплыть по течению и собрать все жёлуди на островах, мимо которых будет проплывать. Увы, течение реки настолько сильное, что он может плыть только вниз по течению. Какое максимальное количество желудей он сможет собрать?
Решите эту задачу, воспользовавшись методом динамического программирования.
4. На столе лежит 25 спичек. Играют двое. Игроки по очереди могут взять от одной до четырёх спичек. Кто не может сделать ход (т. к. спичек не осталось), проигрывает. Другими словами, выигрывает взявший последнюю спичку. Выясните, у кого из игроков есть выигрышная стратегия.
Выигрышная стратегия: брать 5-k предметов, оставляя противнику 20, 15, 10 и 5 предметов.
5. Выясните, у кого из двух игроков есть выигрышная стратегия в такой игре: начальная позиция — на столе лежит 107 спичек, за один ход можно брать 1 или 2 спички. Выигрывает тот, кто взял последнюю спичку.
6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 2, во второй — 3 камня. У каждого игрока неограниченное количество камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает число камней в какой-то куче в 3 раза, или добавляет 3 камня в любую из куч. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 35. Кто выигрывает — игрок, делающий ход первым, или игрок, делающий ход вторым?
В начальный момент в куче было S камней, 1 ≤ S ≤ 46. Выполните следующие задания, в каждом случае обосновывая свой ответ.
1) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения Б, и укажите выигрывающие ходы.
2) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
3) Укажите два значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.
4) Укажите значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, однако у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
В материалах международного конкурса по информатике «Бобёр» есть такая задача, предложенная разработчиками из Нидерландов.
3. В материалах международного конкурса по информатике «Бобёр» есть такая задача, предложенная разработчиками из Нидерландов.
Бобёр Билли любит жёлуди. Он хочет поплыть по течению и собрать все жёлуди на островах, мимо которых будет проплывать. Увы, течение реки настолько сильное, что он может плыть только вниз по течению. Какое максимальное количество желудей он сможет собрать?
Решите эту задачу, воспользовавшись методом динамического программирования.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
ГДЗ по Информатике 11 класс. Моделирование на графах.
§ 11. Моделирование на графах
Вопросы и задания
Бобёр Билли любит жёлуди. Он хочет поплыть по течению и собрать все жёлуди на островах, мимо которых будет проплывать. Увы, течение реки настолько сильное, что он может плыть только вниз по течению. Какое максимальное количество желудей он сможет собрать?
Решите эту задачу, воспользовавшись методом динамического программирования.
В начальный момент в куче было S камней, 1 ≤ S ≤ 46. Выполните следующие задания, в каждом случае обосновывая свой ответ.
1) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения Б, и укажите выигрывающие ходы.
2) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
3) Укажите два значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.
4) Укажите значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, однако у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани.
Моделирование на графах
1. В решении каких прикладных задач используются алгоритмы нахождения кратчайшего пути между заданными вершинами в графе?
2. С помощью алгоритма Дейкстры найдите кратчайший путь между вершинами А и G следующего графа:
3. В материалах международного конкурса по информатике «Бобёр» есть такая задача, предложенная разработчиками из Нидерландов.
Бобёр Билли любит жёлуди. Он хочет поплыть по течению и собрать все жёлуди на островах, мимо которых будет проплывать. Увы, течение реки настолько сильное, что он может плыть только вниз по течению. Какое максимальное количество желудей он сможет собрать?
Решите эту задачу, воспользовавшись методом динамического программирования.
4. На столе лежит 25 спичек. Играют двое. Игроки по очереди могут взять от одной до четырёх спичек. Кто не может сделать ход (т. к. спичек не осталось), проигрывает. Другими словами, выигрывает взявший последнюю спичку. Выясните, у кого из игроков есть выигрышная стратегия.
5. Выясните, у кого из двух игроков есть выигрышная стратегия в такой игре: начальная позиция — на столе лежит 107 спичек, за один ход можно брать 1 или 2 спички. Выигрывает тот, кто взял последнюю спичку.
6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 2, во второй — 3 камня. У каждого игрока неограниченное количество камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает число камней в какой-то куче в 3 раза, или добавляет 3 камня в любую из куч. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 35. Кто выигрывает — игрок, делающий ход первым, или игрок, делающий ход вторым?
7. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 5 камней. Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 15 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 47 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 46. Выполните следующие задания, в каждом случае обосновывая свой ответ.
1) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения »S, и укажите выигрывающие ходы.
2) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
3) Укажите два значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.
4) Укажите значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, однако у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани.