в матема математике что значит
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Так ли точна математика, как кажется?
Наверное, данный вопрос задавал себе каждый, чуточку интересующийся математикой человек. Прочитав статью 2 х 2 = 4, было сделано заключение, что эта тема также может понравиться хабралюдям. Речь пойдет об аксиомах в математике, противоречиях и парадоксах. Кому интересно — добро пожаловать под кат.
Вместо предисловия
Каждый из нас в школе не сомневался в справедливости тех или иных математических утверждений. Ну и правда, что учитель сказал, то и истина. Но, познакомившись со строгой математикой (не люблю слово «высшей»), мы начали понимать, что чем больше мы стараемся формализовать предмет, тем сложнее это сделать, а иногда совсем не получается.
Так нам привычные действительные числа, для Леопольда Кронекера не являлись таковыми, он говорил: «Бог создал натуральные числа, а всё прочее — дело рук человеческих» («Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk»)
После того, как Георг Кантор доказал, что отрезок равномощен (А и B равномощны, если существует биекция между ними) n-мерному пространству, он провозгласил: «Я вижу это, но я не верю в это!» («Je le vois, mais je ne le crois pas!»)
Немного философии
Речь в этой статье пойдет об аксиоматике тех или иных математических множеств, операций и т.д., но все же закономерным вопросом будет, а зачем нам аксиомы вообще нужны? Приведу простой пример. Возьмем русский язык и слово, например, «дежавю». Посмотрим его значение, «Дежавю́ — психическое состояние, при котором человек ощущает, что он когда-то уже был в подобной ситуации». Но мы дотошные, посему теперь вместо одного слова перед нами возникнет куда больше. Что такое «психический», «состояние», «человек», «ощущать», «подобный», «ситуация». Как вы можете заметить, у нас получается дерево слов, а в силу того, что слов, имеющих значение в русском языке конечное множество, у нас получится путь в дереве, в котором встречается дважды одно и то же слово, т.е. мы определили его через самого себя.
Вот для этого и нужны аксиомы. Нам всегда нужен фундамент, с которого мы можем стартовать, что-то, что и так всем интуитивно понятно. Неточность 1. В математике часто бывают утверждения, интуитивно понятные, но приводящие к парадоксам. Например аксиома выбора(Axiom of Choice), но об этом мы поговорим чуть позже.
Больше конкретики. Аксиомы Пеано натуральных чисел.
Я, как программист, люблю считать, что 0 принадлежит натуральным числам, это удобно. Что-ж, теперь наиболее знаменитая аксиоматика Пеано.
1. 0 является натуральным числом.
2. Число, следующее за натуральным, тоже является натуральным.
3. 0 не следует ни за каким натуральным числом.
4. Если натуральное число a непосредственно следует как за числом b, так и за числом c, то b и c совпадают.
5. (Аксиома индукции) Если какое-либо предложение доказано для 0 (база индукции) и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
Разберемся по-порядочку.
1-я аксиома говорит, что существует хотя бы одно натуральное число. Иначе бы мы сказали, что это вообще пустое множество и все аксиомы бы для него выполнялись бы.
2 и 3 вроде бы и так ясны.
4. Эта аксиома нужна для того, чтобы не появились «ответвления». Иначе мы могли бы сказать, что 3 следует за 2 и 2′, а дальше 2 и 2′ за 1 и 1′ соответственно, и т.д. В принципе, такая модель имеет право на существование, но на ней крайне сложно ввести отношение порядка.
5. Первый человек в очереди женщина. За каждой женщиной идет женщина. В реальной жизни это значит, что вся очередь состоит из женщин. А так как мы хотим описывать все же более жизненные объекты, то и вводим аксиому индукции, ибо из предыдущих она никак не следует.
Удобная модель, все отлично, все счастливы. Вопрос, в чем же подвох? Оказывается, что если мы добавим новое натуральное число с к нашим привычным натуральным числам и скажем, что оно больше всех наших привычных, то мы не придем ни к какому противоречию. Т.е. у нас есть не только наша модель N, но и, к примеру, N + Z. Где в N и Z (целые числа) обычное сравнение чисел, а также любое число из N меньше любого числа из Z.
Вопрос, можно ли ввести аксиомы так, чтобы мы описали наши привычные натуральные числа, и только их (т.е. существует ли формула, подставив в которую естественное натуральное число она выдаст True, а любое другое число False)? Ответ — нет. Идея доказательства в том, что все формулы можно закодировать натуральными числами. А далее, написав хитрую формулу, и подставив ее код в Ф (формула, которая по предположению умеет определять естественную натуральность), мы получим противоречие.
Больше конкретики. Аксиоматика множеств Цермело-Френкеля (ZF)
1. Аксиома объемности. Если два множества состоят из одинаковых элементов, то они равны.
2. Аксиома подмножеств. Если у нас есть некоторая формула, то из любого множества она «вырезает» также множество.
3. Аксиома замены. Если для каждого мн-ва х, F(x) = также является множеством, то для любого а, — также множество.
4. Аксиома степени. Множество подмножеств также является множеством.
5. Аксиома бесконечности. Существует множество, которое содержит пустое множество, а также вместе с каждым элементом x содержит множество <
6. Аксиома регулярности. Не существует бесконечных по включению цепочек множеств, т.е. нельзя, чтобы множество a1 сожержало a2, то в свою очередь a3, и т.д.
Противоречия и парадоксы
Во-первых, не доказано, что аксиомы ZF непротиворечивы, если же они противоречивы, то можно вывести любое утверждение, например 0 = 1, и грош цена нашей науке. Даже более, доказано, что нельзя доказать непротиворечивость ZF. Забавная штука получается, но в этом нет ничего страшного. Если мы чего-то не можем доказать, не значит, что этого нет, в данном случае непротиворечивости. Движемся дальше.
Математика получается достаточно скупой наукой, то есть мало всего можно доказать, если не добавить аксиому выбора. А что это за аксиома такая? В трех словах — из любого непустого множества можно выбрать элемент. Казалось бы, очень естественная аксиома, но она приводит к парадоксу Банаха-Тарского, заключающегося в том, что шар можно разбить на 5 кусков и собрать из них 2 таких же шара. Т.е. яблоко можно разрезать на 5 частей и собрать два яблока?! Посему и парадокс. Что еще интереснее, доказано, что если теория ZF непротиворечива, то добавив к ней аксиому выбора (ZF + Axiom of Choice = ZFC) мы получим непротиворечивую аксиоматику!
Искорка надежды
То мы что-то не можем доказать, то какие-то парадоксы. Может, математика — полная чушь? Может не следует ее изучать? Ответ: никакая не чушь, изучать следует. Почему же, спросит читатель. Я приведу достаточно физическое доказательство. Обычно в физике бывает так. «Ого, в течении 100 лет мы наблюдали за падением бутербродов и оказалось, что они падают маслом вниз, назовем это законом». Думаете, шучу? А попытайтесь доказать, что тела состоят из молекул. Ничего более строгого, чем то, что в течение 2000 лет эта теория не давала сбой, вы не придумаете. Так вот с математикой примерно та же ситуация. Мы используем ее, вроде бы машины едут, самолеты летят, здания стоят и все хорошо. Интуитивно ясно, что если бы в математике было противоречие, то, чем глубже бы мы копались в дебрях этой науки, тем легче бы были доказательства теорем, но такого не происходит.
И все же, откуда парадокс Банаха-Тарского возникает, все же достаточно логично! На самом деле, если аккуратно заметить, то во Вселенной нет ничего бесконечного. Нет ничего бесконечно малого и т.д. Просто удобно работать с бесконечными множествами. Так что вполне нормально, что могут получаться результаты не применимые к жизни.
Зачем нужна математика
Интересные факты про математику
Математика — это не только арифметические задачки. Это особый язык, который учит думать и рассуждать.
Математику называют междисциплинарной наукой, потому что она тесно связана с физикой, географией, геологией, химией. Социология и экономика неотделимы от математики, поэтому многие выводы из гуманитарных исследований опираются на математические понятия и логические законы.
Мир изменился и стал более технологичным, поэтому для любителей математики открыто множество вариантов профессионального развития.
Если 15 лет назад перспективными были сферы маркетинга и юриспруденции, то сегодня лидирует IT.
Профессиональная востребованность = понимание технологий + способность к решению нестандартных задач. И ключ к успеху — знание математики.
Что отличает математику от других школьных предметов:
Математика развивает мышление
Зачем заниматься физкультурой? Ответ простой — для здоровья и красоты тела.
Зачем учить математику? Ответ на этот вопрос кажется менее очевидным.
Математика — это гимнастика для ума. Хочешь не хочешь, но в процессе изучения будут крепчать качества, которые влияют на способ мышления. Для этого не обязательно учиться в профильном классе и участвовать в олимпиадах — решение даже самых простых задачек на пропорции или с процентами дает значительный эффект.
Обобщение, сокращение, анализ, систематизация, выделение важного, поиск закономерностей, формулирование гипотез и доказательство теорий — все это помогает развить мышление, сделать его более гибким. Точно также, как физические упражнения делают наше тело подвижнее, дают заряд сил и тренируют выносливость, математика тренирует ум.
Математика развивает интеллект. Набор правил и функций, которые мы изучаем в школе, делают наше мышление последовательным и логичным. Это отражается на умении рассуждать, формулировать мысли и замечать взаимосвязи. И самое увлекательное, что эти знания можно (и нужно!) применять не только в школе, но и в нестандартных ситуациях: чтобы выбрать самую выгодную банковскую карту, просчитать литры краски для ремонта или создать карту сокровищ, чтобы не забыть где они спрятаны.
Математика — универсальный международный язык, которым владеют почти все люди на земле. Эти знания пригодятся в любой стране и могут стать предметом интересной беседы.
Что понять, зачем учить математику в школе, только представьте, как приятно, когда в голове нет «каши» и путаницы в рассуждениях. На этот счет еще в прошлом веке великий учёный Ломоносов сказал: «Математику только затем учить надо, что она ум в порядок приводит». Как тут можно спорить? 😇
Математика формирует характер
Чтобы правильно решать математические задачи, недостаточно одних лишь знаний. Нужны такие качества характера, как внимательность, настойчивость, последовательность, точность и аккуратность. Чем регулярнее мы практикуемся, тем сильнее укрепляются эти черты. И еще бонус: эти качества можно применять не только на уроках в школе, но и в других сферах жизни.
Чем сложнее математические задачи, тем больше усилий и навыков нужно приложить для их решения.
Благодаря математике можно избавиться от вредных привычек:
Домысливать и не уметь объяснять, почему думаешь именно так
Оперировать фактами и точными терминами и быть более убедительным
Запоминать информацию механически, «зазубривать»
Оценивать, анализировать, строить аналогии и подвергать критике
Математика тренирует память
Ученые из Стэнфордского университета в США изучили, как человек решает математические задачи и выяснили, что взрослые люди используют для этого навык «доставать» из памяти ответы на основе прошлого опыта.
Почему учителя настаивают на регулярном посещении уроков? Дело не в их вредности, а в том, что при решении математических задач, мы «достаем» из памяти ответы на основе прошлого опыта. А чтобы этот опыт закрепить, нужно повторять материал и тренироваться в решении примеров. Только так можно запомнить все правила и формулы. 🤓
В журнале Nature Neuroscience в 2014 году опубликовали исследование про роль определенных областей головного мозга в развитии познавательной активности детей. Оказалось, что на интерес к знаниям оказывает сильное влияние гиппокамп — часть мозга, которая отвечает за память.
Интересный факт! Определенные области головного мозга влияют на развитие познавательной активности детей. Например, на интерес к знаниям влияет часть мозга, которая отвечает за память — гиппокамп. Поэтому:
Математика — волшебница, не иначе! Систематизируем все волшебные свойства и повторим, какие навыки можно развить с помощью математики:
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Благодаря математике символ «Х» прочно ассоциируется у многих людей с чем-то таинственным и загадочным. Это неудивительно, ведь по правилам царицы наук так принято обозначать некую неизвестную величину, которую необходимо найти. Сегодня не существует однозначного ответа о природе происхождения этого математического символа, однако есть несколько гипотез, авторы которых пытаются объяснить эту загадку.
История появления в математике буквы X
Впервые решил обозначать неизвестное число буквенным символом еще в III веке известный математик из Александрии – Диофант. В его системе альфа с чертой означала единицу, бета двойку и так далее. С (йота) он начинал считать десятки, а с P (ро) сотни. Завершала числовой ряд 27-я буква Т (сампи), которая означала 900. При этом следующей букве сигме концевой своего числа не досталось, поэтому Диофант посчитал логичным использовать именно ее в качестве символа неизвестного числа.
Арабская группа народов прославилась многими научными открытиями, среди которых особняком стоят достижения в области математики. Как считается, именно в странах Ближнего Востока были созданы уравнения и десятичные дроби, местные ученые научились извлекать корни и придумали термин «алгебра», который дословно переводится как «учение об отношениях, перестановках и решениях».
Появление алгебры связано с деятельностью талантливого выходца из Хорезма Аль-Хорезми, который изучал способы решения математических уравнений. В своих трудах исследователь описывал ход мыслей словами, не используя цифровых и буквенных символов для обозначения формул. Если встречались неизвестные величины он их записывал как «шеи», что по-арабски означает какая-то вещь. Этому слову в местном языке соответствовал знак Х. После завоевания арабами Пиренейского полуострова начинается процесс культурной интеграции с местным населением. Среди множества книг испанцы перевели сочинения Аль-Хорезми. В европейском варианте неизвестное написали как xei. Для большего удобства записи формул обозначение сократили до одной первой буквы и получилось «Х».
Версия №2 «Европейская»
Продолжил дело александрийского ученого Диофанта француз Франсуа Виет (1540-1603), ставший основоположником символической алгебры. Он ввел в научный оборот буквенные символы для написания величин. Ряд гласных букв (a, I, o, u, e) для известных, а согласные для неизвестных (c, b, d, f).
Привычные нам сегодня обозначения — буквы начала латинского алфавита как известные величины (a, b, c, d) и последние буквы как неизвестные (x, y, z) впервые употребил в XVII веке известнейший французский мыслитель Рене Декарт (1596-1660), который стоял у истоков аналитической геометрии.
В его труде «Геометрия», который был опубликован в 1637 году и является единственным, посвященным исключительно математике, автор упоминает заимствованный у испанцев символ «Х». На французском языке он произносился «кс» и именовался «икс». Так как неизвестная величина в большинстве математических выражений одна, чаще всего употребляли именно «Х», что позволило этому символу обойти по популярности другие.
Над символом неизвестности прямо или косвенно поработали ученые разных стран и эпох. Диофант и Виет предложили принцип буквенного обозначения цифр. К этой же мысли пришел арабский математик Аль-Хорезми, а после перевода его книг испанцами в XI веке европейцы получили обозначение «Х». В XVII веке его ввел в широкий научный оборот Р. Декарт.
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
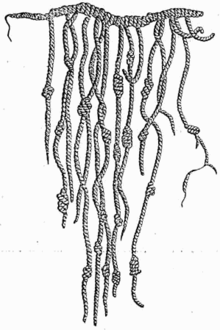
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Целые ( ) • Рациональные ( ) • Рациональные ( ) • Алгебраические ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Комплексные ( ) • Кватернионы ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 | 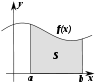 |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 |  |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.








 masterok
masterok