в кубе все ребра равны 5 на его ребре bb1 отмечена точка k так что

Задание 14. Математика ЕГЭ. В кубе ABCDA1B1C1D1 все ребра равны 5. На его ребре BB1 отмечена точка K так, что KB =4. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.

Задание.

В кубе ABCDA₁B₁C₁D₁ все ребра равны 5. На его ребре BB₁ отмечена точка K так, что KB =4. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.

а) Докажите, что A₁P:PB₁ = 3:1, где P – точка пересечения плоскости α с ребром A₁B₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

Решение:

а) Докажите, что A₁P:PB₁ = 3:1, где P – точка пересечения плоскости α с ребром A₁B₁.

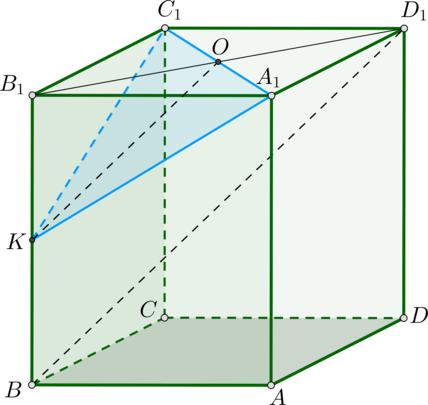
Построим плоскость α, проходящую через точки K и C₁ параллельно прямой BD₁. Для этого построим плоскость, содержащую прямую BD₁, т.е проходящую через точки B, B₁, D, D₁.

Точки K и C₁ лежат в одной плоскости, поэтому можно провести KC₁. Точка К лежит в плоскости BDD₁, проведем прямую KE параллельно BD₁. Эта прямая пересекает прямую B₁D₁ в точке E.

Точки Е и C₁ лежат в одной плоскости, проведем прямую C₁E. Прямая C₁E пересекает A₁B₁ в точке P.

Точки P и K лежат в одной плоскости, проведем PK. Плоскость KPC₁ – искомое сечение.

Треугольники BB₁D₁ и KB₁E – подобные треугольники, тогда

Рассмотрим рисунок, так как MENB₁ – квадрат, то EM = 1. Треугольники PB₁C₁ и PME – подобные треугольники, тогда

B₁C₁ = 5, пусть PB₁ = x, тогда PM = x — 1

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

Треугольник B₁KC₁ – прямоугольный.

Пусть точка H – основание высоты B₁H треугольника B₁KC₁.

B₁H – проекция наклонной PH на плоскость BB₁C₁.

Тогда по теореме о трех перпендикулярах PH перпендикулярна KC₁.

Следовательно, угол PHB₁ – линейный угол искомого двугранного угла.

Треугольник PB₁H – прямоугольный, тогда

Найдем площадь треугольника B₁KC₁:

Площадь треугольника B₁KC₁ найдем другим способом:

Источник

В кубе все ребра равны 5 на его ребре bb1 отмечена точка k так что

Задание 14. В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре ВВ1 отмечена точка K так, что KB=3. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.

а) Докажите, что A1P:PB1 =2:1, где Р — точка пересечения плоскости α с ребром А1В1.

б) Найдите угол наклона плоскости α к плоскости грани ВВ1С1C.

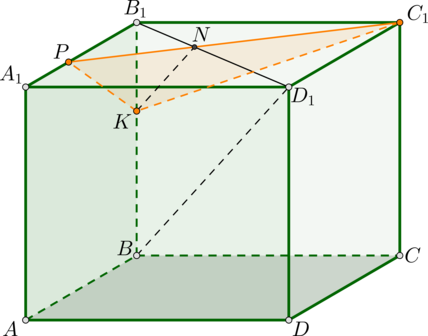
а) Проведём через точку K прямую, параллельную BD1. Пусть эта прямая пересекает плоскость грани A1B1C1D1 в точке L. Прямая KL лежит в плоскости BB1D1, значит, точка L лежит на диагонали B1D1. Более того, B1L:LD1 =В1K:KB=1:3.

Прямая C1L пересекает ребро А1В1 в точке Р, принадлежащей плоскости α. Треугольники B1LP и D1LC1 подобны, поэтому B1P:D1C1=B1L:D1L=1:3. Значит, A1Р:РВ1 =2:1.

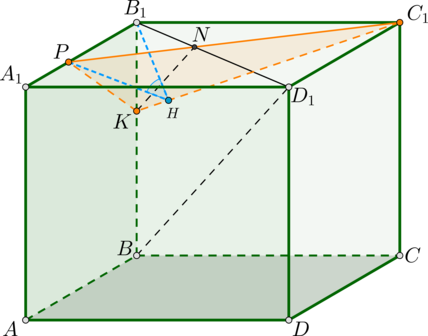
б) Опустим из точки перпендикуляр В1Н на C1K. По теореме о трёх перпендикулярах прямые РН и C1K перпендикулярны. Значит, угол B1HP искомый.

Поскольку А1Р:РВ1 = 2:1, получаем PB1 = 4/3. В прямоугольном треугольнике B1C1K:

.

.

Ответ: .

Источник

В кубе все ребра равны 5 на его ребре bb1 отмечена точка k так что

В кубе ABCDA₁B₁C₁D₁ все рёбра равны 7. На его ребре BB₁ отмечена точка K так. что KB = 4. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

Это задание ещё не решено, приводим решение прототипа.

В кубе ABCDA₁B₁C₁D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

а) В плоскости через точку К проведем прямую параллельно Пусть эта прямая пересекает диагональ в точке L. В плоскости основания проведем прямую пусть она пересекает сторону в точке P. Треугольник KPC₁ — сечение, проходящее через точки К и С₁ параллельно прямой BD₁. Действительно, прямая BD₁ параллельна плоскости сечения, так как параллельна лежащей в нем прямой KL.

В плоскости основания через точку A₁ проведем прямую параллельно C₁P. Пусть она пересекает D₁В₁ в точке М. По теореме Фалеса имеем: и поэтому Тогда Что и требовалось доказать.

б) Пусть теперь точка N — основание высоты прямоугольного треугольника — является проекцией наклонной PN на плоскость Тогда угол PNB₁ — линейный угол искомого двугранного угла. Имеем:

Тем самым,

Ответ: б)

Приведём другое решение.

б) Уравнение плоскости — ax + by + cz + d = 0.

Приведём координаты точек C₁(0; 4; 4), K(4; 4; 3),

Подставив координаты указанных точек в уравнение, получим систему трёх уравнений

Вычтем из первого уравнения второе, из первого третье, из второго третье, получим следующую эквивалентную систему уравнений:

Таким образом, вектор нормали плоскости имеет вид Откуда имеем: a = 1, b = 3, c = 4. Получаем уравнение плоскости: x + 3y + 4z + d = 0. Определим теперь коэффициент d, для этого подставим в это уравнение координаты точки C₁:

Имеем: x + 3y + 4z – 28 = 0 — уравнение плоскости PKC₁. Координаты вектора нормали к плоскости Координаты вектора нормали к плоскости Обозначим угол между плоскостями и как Найдём косинус угла между плоскостями и

Откуда Может также быть получен ответ и через арктангенс:

Приведём идею решения Евгения Матвеева.

Введём систему координат с центром в точке Уравнение плоскости сечения C₁PK в отрезках Нормальный вектор к этой плоскости: нормальный вектор к плоскости BB₁C₁C: Тогда

Источник

В кубе все ребра равны 5 на его ребре bb1 отмечена точка k так что

В кубе ABCDA₁B₁C₁D₁ все рёбра равны 7. На его ребре BB₁ отмечена точка K так. что KB = 4. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

Это задание ещё не решено, приводим решение прототипа.

В кубе ABCDA₁B₁C₁D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

а) В плоскости через точку К проведем прямую параллельно Пусть эта прямая пересекает диагональ в точке L. В плоскости основания проведем прямую пусть она пересекает сторону в точке P. Треугольник KPC₁ — сечение, проходящее через точки К и С₁ параллельно прямой BD₁. Действительно, прямая BD₁ параллельна плоскости сечения, так как параллельна лежащей в нем прямой KL.

В плоскости основания через точку A₁ проведем прямую параллельно C₁P. Пусть она пересекает D₁В₁ в точке М. По теореме Фалеса имеем: и поэтому Тогда Что и требовалось доказать.

б) Пусть теперь точка N — основание высоты прямоугольного треугольника — является проекцией наклонной PN на плоскость Тогда угол PNB₁ — линейный угол искомого двугранного угла. Имеем:

Тем самым,

Ответ: б)

Приведём другое решение.

б) Уравнение плоскости — ax + by + cz + d = 0.

Приведём координаты точек C₁(0; 4; 4), K(4; 4; 3),

Подставив координаты указанных точек в уравнение, получим систему трёх уравнений

Вычтем из первого уравнения второе, из первого третье, из второго третье, получим следующую эквивалентную систему уравнений:

Таким образом, вектор нормали плоскости имеет вид Откуда имеем: a = 1, b = 3, c = 4. Получаем уравнение плоскости: x + 3y + 4z + d = 0. Определим теперь коэффициент d, для этого подставим в это уравнение координаты точки C₁:

Имеем: x + 3y + 4z – 28 = 0 — уравнение плоскости PKC₁. Координаты вектора нормали к плоскости Координаты вектора нормали к плоскости Обозначим угол между плоскостями и как Найдём косинус угла между плоскостями и

Откуда Может также быть получен ответ и через арктангенс:

Приведём идею решения Евгения Матвеева.

Введём систему координат с центром в точке Уравнение плоскости сечения C₁PK в отрезках Нормальный вектор к этой плоскости: нормальный вектор к плоскости BB₁C₁C: Тогда

Источник

Задачи по стереометрии прошлых лет (страница 4)

а) Докажите, что сечение призмы плоскостью \(\alpha\) является равнобедренным треугольником.

(ЕГЭ 2015, резервный день)

Таким образом, \(A_1KC_1\) – искомое сечение. Из равенства боковых граней следует, что отрезки \(KC_1\) и \(KA_1\) равны, то есть треугольник \(A_1KC_1\) равнобедренный.

б) Найдем по теореме Пифагора \(KA_1\) :

Таким образом, периметр

(ЕГЭ 2015, досрочная волна)

\[\dfrac=\dfrac=\dfrac23 \quad \Rightarrow \quad PB_1=\dfrac23C_1D_1=\dfrac23A_1B_1.\]

\[V_=\dfrac13\cdot PB_1\cdot \dfrac12KB_1\cdot B_1C_1= \dfrac13\cdot \dfrac23\cdot 5\cdot \dfrac12\cdot 2\cdot 5=\dfrac<50>9.\]

Тогда объем большей части равен

(ЕГЭ 2015, досрочная волна)

\[\dfrac=\dfrac=\dfrac23 \quad \Rightarrow \quad PB_1=\dfrac23C_1D_1=\dfrac23A_1B_1.\]

\[S_=\dfrac12KB_1\cdot B_1C_1=\dfrac12B_1H\cdot KC_1 \quad \Rightarrow \quad B_1H=\dfrac<10><\sqrt<29>>\]

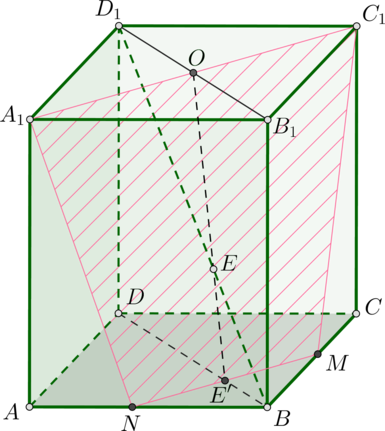
(ЕГЭ 2015, пробный вариант)

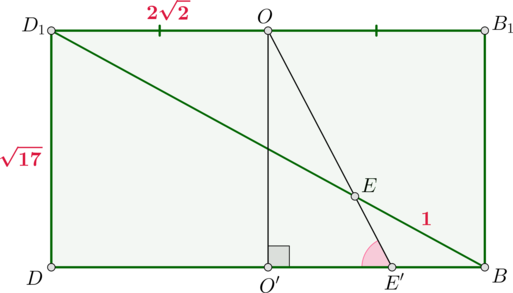
Заметим также, что \(\triangle EE’B\sim \triangle EOD_1\) по двум углам. Следовательно, \[\dfrac=\dfrac \quad\Rightarrow\quad E’B= \dfrac<\sqrt2>3.\] Следовательно, \[E’O’=2\sqrt2-\dfrac<\sqrt2>3=\dfrac<5\sqrt2>3.\] Следовательно, \[\mathrm\,\angle OE’O’=\dfrac= \dfrac<\sqrt<17>><\frac<5\sqrt2>3>=0,3\sqrt <34>\quad\Rightarrow\quad \angle OE’O’=\mathrm\,(0,3\sqrt<34>).\]

Источник