Кумулятивная функция что это
Кумулятивные функции распределения
Кумулятивные функции распределения
Кумулятивная функция распределения дает интегральную картину распределения вероятности. Она рассматривает функцию вероятностной меры типа колоколообразной кривой и задает вопрос: «Какова вероятность того, что результат окажется меньше или равен такому-то?» Нормальная кривая показывает вероятность конкретного значения, a кумулятивная функция – вероятность данного спектра значений. Кумулятивная функция позволяет объединить понятие о неопределенности (теорию вероятности) с нашим инструментом для принятия решений (дерево решений). Она охватывает весь спектр возможных исходов при анализе переменных с множественными значениями.
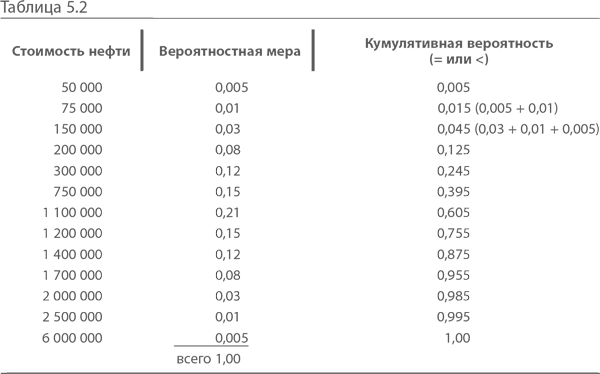
Вернемся к примеру с нефтяной скважиной и посмотрим распределение значений возможной стоимости нефти (табл. 5.2):
Построив функцию кумулятивного распределения, человек, принимающий решение, устанавливает среднее, то есть ожидаемую стоимость, и с этого может начать анализ. Построение кумулятивного распределения позволяет объединить оценки вероятности верхней границы, середины и нижней границы спектра исходов и установить ожидаемую стоимость, что позволит принять решение.
Диапазон вероятностей от 0 до 1,0 кумулятивного распределения разбивается на части – квантили – методом медиан интервального ряда. В таблице именно так разделена ожидаемая стоимость. Например, чтобы разделить диапазон вероятности ожидаемой стоимости на пять частей, нужно взять квантили 0,1; 0,3; 0,5; 0,7 и 0,9. Эти квантили будут представлять собой среднее арифметическое в диапазонах значений 0–0,2; 0,2–0,4; 0,4–0,6; 0,6–0,8 и 0,8–1,0 соответственно.
Чтобы объединить концепцию кумулятивного распределения с деревом решения и принимать существенные управленческие решения, нужно представить себе все вероятные значения прибыли от нефтяной скважины. Диапазон значений можно изобразить в виде веера событий. Кому-то может не хватить терпения для представления бесконечных возможностей в виде ветвей дерева, и тут выручит кумулятивная вероятность.
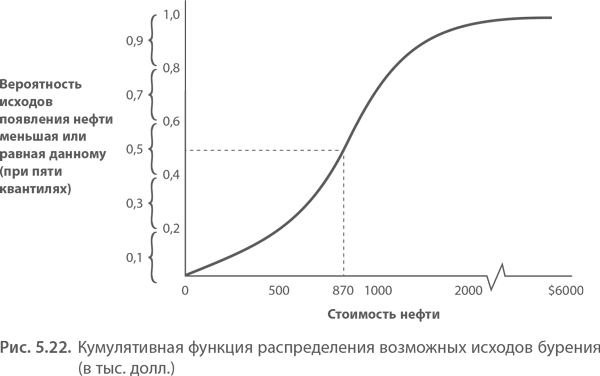
Рисуем кумулятивное распределение. Чтобы представить кумулятивное распределение в графической форме, как показано ниже, следует опираться на собственное суждение и данные исследований. Нужно задать себе ряд вопросов:
• При каком значении в 50 % случаев результат оказывается выше или ниже заданного значения (медиана)?
• Каким будет значение нижнего конца спектра (квантиль 0,10)?
• Каким будет значение верхнего конца спектра (квантиль 0,90)?
Ответив на эти вопросы, вы сможете представить кумулятивную стоимость возможных исходов. Ограничившись пятью исходами или пятью квантилями кумулятивного распределения, вы можете изобразить веер событий и их вероятностей на дереве решений в виде пяти ветвей.
Ожидаемый денежный эквивалент будет таким же, как при первом рассмотрении, но только потому, что с самого начала для удобства была задана правильная величина ожидаемой стоимости.
Сокращенный вариант такого анализа называют методом Тьюки – Пирсона. Вместо пяти квантилей используется всего три – 0,05; 0,5 и 0,95. Соответствующие этим квантилям вероятности – 0,185; 0,63 и 0,185.
Применительно к крупным задачам дерево решений строится с помощью компьютерных симулякров Монте-Карло, самый популярный из них – Oracle. Дерево и параметры «веера событий» кумулятивного распределения включены в компьютерную модель. Программа прогоняет множество сценариев событий, чтобы дать вам представление, чем может обернуться дело. Некоторые из компаний Fortune 500 используют этот метод.
Кумулятивное распределение и анализ методом квантилей можно применять к ситуациям, в которых ожидаемая стоимость ветви дерева решений неопределенна. Однако важнее всего суждение аналитика. Дерево – это всего лишь инструмент, который МВА обязан использовать в сочетании со своими знаниями и интуицией.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
1.1. Сущность, функции и принципы формирования и распределения прибыли в деятельности коммерческих организаций
1.1. Сущность, функции и принципы формирования и распределения прибыли в деятельности коммерческих организаций В реальной жизни прибыль – конечная цель и движущий мотив производства и рыночной экономики. Это главная надежда и основной показатель эффективности любой
Расчет оптимального распределения
Расчет оптимального распределения Прежде всего, давайте определимся с тем, что мы имеем в виду, когда говорим об оптимальном распределении. По сути, речь может идти об одном из трех видов распределения: будущем, гипотетическом или историческом. Вы можете определить
8. Внедрение стратегии распределения активов
8. Внедрение стратегии распределения активов В фильме «Цельнометаллическая оболочка» (Full Metal Jacket) Стэнли Кубрика есть памятный эпизод, связанный с приключениями морских пехотинцев во Вьетнаме. Сюжет раскручивается вокруг молодого неопытного журналиста, который
33. Характеристика закономерности рядов распределения
33. Характеристика закономерности рядов распределения С помощью рядов распределения решается важнейшая задача статистики – характеристика и измерение показателей колеблемости для варьирующих признаков.В вариационных рядах существует определенная связь в изменении
Логистика физического распределения товаров
1. Статистические ряды распределения
1. Статистические ряды распределения В результате обработки и систематизации первичных данных статистического наблюдения получают группировки, называемые рядами распределения.Статистические ряды распределения представляют собой упорядоченное расположение единиц
2. Графическое изображение рядов распределения
2. Графическое изображение рядов распределения Анализ рядов распределения можно проводить на основе их графического изображения. Линейчатые и круговые диаграммы строятся для отображения структуры совокупности.Применяются вместе с диаграммами и такие линии, как
2. Характеристика закономерности рядов распределения
2. Характеристика закономерности рядов распределения С помощью рядов распределения решается важнейшая задача статистики – характеристика и измерение показателей колеблемости для варьирующих признаков.В вариационных рядах существует определенная связь в изменении
Диагностика распределения времени
Диагностика распределения времени Уже много десятилетий назад мы осознали: чтобы понять, куда уходит время, и прежде чем пытаться им управлять, нужно регистрировать его затраты и распределение. Принципы научной организации труда, внедренные в США еще в начале прошлого
Нам не нужна политика распределения пространства
Нам не нужна политика распределения пространства Мы часто перестраиваем нашу «фабрику» – раз в неделю, иногда каждый день. Удачное расположение проводки и легкие столы позволяют любому члену команды сменить место, как только возникнет такая необходимость. В Menlo нет
Методы распределения
Методы распределения Метод личных продаж используется для организации дистрибьюторской сети и обеспечения поддержки реселлеров независимо от того, на каком рынке реализуется продукция – потребительском или промышленном. При этом функциональные обязанности
Каналы поставок и распределения
Каналы поставок и распределения Имеющиеся в вашей отрасли каналы поставок и распределения способны сыграть решающую роль в успехе компании. В одних отраслях трудно получить доступ к дистрибуции, в других ограничено число надежных источников поставок. В отраслях, где
5. Оптимизация каналов распределения
5. Оптимизация каналов распределения «Когда я впервые приехал в Непал 3 года тому назад, то каждый человек, с которым мне приходилось разговаривать, сообщал мне, что презервативы теперь продаются везде. Поэтому я удивился, почему меня попросили приехать в эту страну
Решения по каналу распределения
Решения по каналу распределения Решения по каналу распределения влияют на то, где, как и когда будет осуществлена доставка ваших предложений и обеспечен доступ к ним для потребителей. Эти решения включают в себя также «атмосферу» вокруг процесса обмена –
Кумулятивная функция распределения
Кумуляти́вная фу́нкция распределе́ния (или просто функция распределения) в теории вероятностей однозначно задаёт распределение случайной величины или случайного вектора.
Содержание
Определение
Пусть дано вероятностное пространство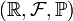 
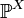
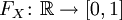
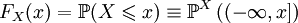
, и на нём определена случайная величина X с распределением 
. Тогда функцией распределения случайной величины X называется функция 
, задаваемая формулой:
.
Свойства
Тождества
Из свойств вероятности следует, что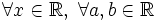 
, таких что a :
Дискретные распределения
Если случайная величина X дискретна, то есть её распределение однозначно задаётся функцией вероятности
,
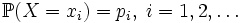
то функция распределения FX этой случайной величины кусочно-постоянна и может быть записана как:
.
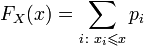
Непрерывные распределения
,
,
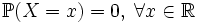
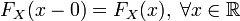
а следовательно формулы имеют вид:
,
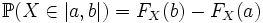
где | a,b | означает любой интервал, открытый или закрытый, конечный или бесконечный.
Абсолютно непрерывные распределения
.
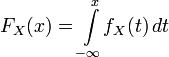
Функция fX называется плотностью распределения. Известно, что функция абсолютно непрерывного распределения непрерывна, и более того если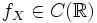 
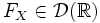
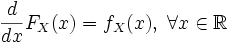
, то 
, и
.
Вариации и обобщения
Многомерные функции распределения
Пусть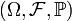 
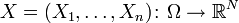
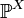
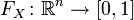
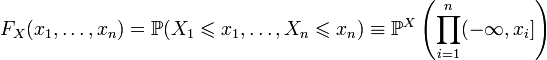
фиксированное вероятностное пространство, и 
— случайный вектор. Тогда распределение является вероятностной мерой на 
. Функция этого распределения 
задаётся по определению следующим образом:
,
где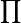 
в данном случае обозначает декартово произведение множеств.
См. также
Полезное
Смотреть что такое «Кумулятивная функция распределения» в других словарях:
Распределения вероятностей — Распределение вероятностей это закон, описывающий область значений случайной величины и вероятности их принятия. Содержание 1 Определение 2 Способы задания распределений 2.1 Дискрет … Википедия
ЭМПИРИЧЕСКАЯ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ — (frequency distribution) Функция, описывающая распределение случайных значений переменной. Если переменная х принимает значения на непрерывном отрезке и имеет минимальное значение а и максимальное значение b, эмпирическая плотность распределения… … Экономический словарь
Кривая видового накопления — графическое представление числа видов, найденных на определенной территории (или в определенном биотопе и т. п.), как функции от кумулятивной совокупности исследовательских усилий, направленных на их нахождения. Исследовательское усилие может… … Википедия
Непрерывность (математика) — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Непрерывные функции — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Непрерывный оператор — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Непрерывный функционал — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Разрыв второго рода — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Разрыв первого рода — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Свойства функций, непрерывных в точке — Непрерывное отображение или непрерывная функция это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения. Это понятие определятся немного по разному в различных разделах математики;… … Википедия
Кумулятивная функция распределения в нормально распределенных данных
В данной статье объясняется, как получить кумулятивную функцию распределения Гаусса и почему она полезна в статистическом анализе.
Если вы только присоединяетесь к нашему обсуждению статистики в электротехнике, возможно, вам будет интересно сначала просмотреть предыдущие статьи этой серии, список которых можно найти в оглавлении вверху над статьей.
Что мы знаем из предыдущих статей:
Если участки интегрирования функции плотности вероятности являются ключом к извлечению вероятностей из измеренных данных, можно задаться вопросом о возможности простого интегрирования всей функции и тем самым создания новой функции, которая даст нам прямой доступ к информации о вероятности.
Как оказалось, это стандартный метод статистического анализа, и эта новая функция, которую мы получаем путем интегрирования всей функции плотности вероятности, называется кумулятивной функцией распределения.
Кумулятивная функция нормального распределения
Использование кумулятивной функции распределения (CDF, cumulative distribution function) является особенно хорошей идеей, когда мы работаем с нормально распределенными данными, потому что интегрировать гауссову кривую не так-то просто.
Фактически, чтобы получить кумулятивную функцию распределения кривой Гаусса, даже математики должны прибегнуть к численному интегрированию (функция \(e^<-x^2>\) не имеет первообразной, которая может быть выражена в элементарной форме). Это означает, что кумулятивная функция распределения Гаусса на самом деле представляет собой последовательность дискретных значений, созданных из множества отдельных выборок, взятых вдоль гауссовой кривой.
В эпоху компьютеров мы можем легко обрабатывать огромное количество выборок, и, следовательно, дискретная кумулятивная функция распределения, полученная путем численного интегрирования, может быть вполне адекватной заменой непрерывной функции, полученной посредством символьного интегрирования.
Если мы отложим на графике большое количество значений гауссовой функции распределения, кривая будет выглядеть следующим образом:
Рисунок 1 – Кумулятивная функция нормального распределения
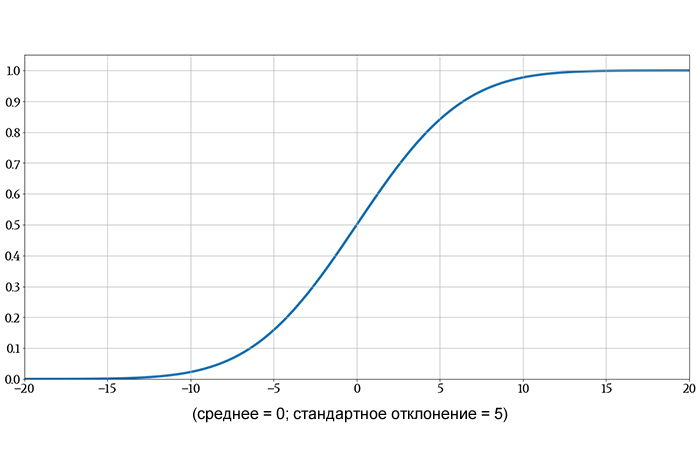
На следующем графике показаны как исходная гауссова функция плотности вероятности, так и ее функция распределения, чтобы вы могли увидеть, как интегрирование превращает одно в другое.
Рисунок 2 – Функция плотности вероятности нормально распределенной переменной и соответствующая функция распределения
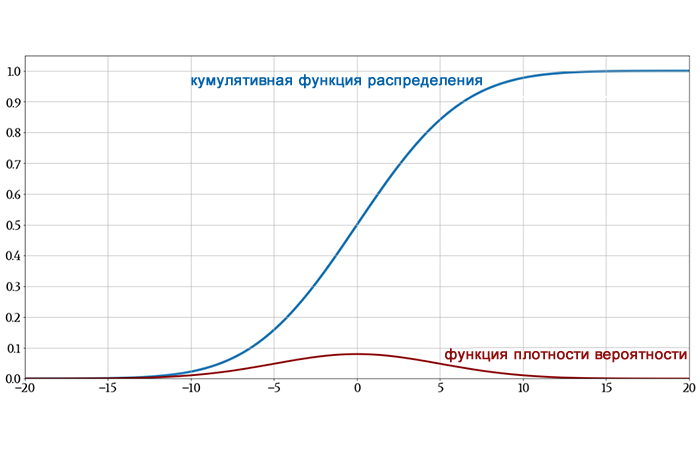
Одно небольшое замечание, прежде чем мы продолжим: в обсуждениях о статистике вы можете увидеть символ Φ (заглавная греческая буква фи). Когда нормальное распределение имеет среднее значение 0 и стандартное отклонение 1, оно называется стандартным нормальным распределением. Кумулятивная функция стандартного нормального распределения обозначается Φ; таким образом,
Пример кумулятивной функции распределения
Когда мы интегрируем функцию плотности вероятности от отрицательной бесконечности до некоторого значения, обозначенного z, мы вычисляем вероятность того, что результат случайно выбранного измерения или нового измерения попадет в числовой интервал, который простирается от отрицательной бесконечности до z. Другими словами, мы вычисляем вероятность того, что измеренное значение будет меньше z.
Это именно та информация, которую мы получаем из кумулятивной функции распределения и без необходимости интегрирования. Если мы посмотрим на график кумулятивной функции распределения и найдем вертикальное значение, соответствующее некоторому числу z на горизонтальной оси, мы узнаем вероятность того, что измеренное значение будет меньше z.
Рисунок 3 – Определение вероятности того, что измеренное значение будет меньше некоторой величины, с помощью кумулятивной функции распределения
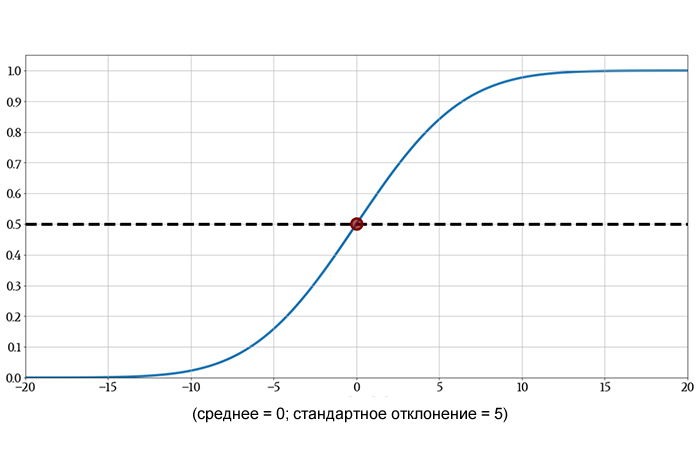
Кумулятивная функция распределения при z = 0 равна 0,5. Это говорит нам о том, что результат выбранного случайным образом измерения имеет 50% вероятность быть меньше нуля. Это интуитивно понятно: нормальное распределение симметрично относительно среднего, и поскольку среднее значение в этом случае равно нулю, любое отдельное измерение имеет равные шансы быть меньше или больше нуля.
Кумулятивная функция распределения (CDF) также обеспечивает простой способ определения вероятности того, что результат измерения попадет в определенный диапазон. Если диапазон определяется двумя значениями z1 и z2, всё, что нам нужно сделать, это вычесть значение функции распределения в z2 из значения функции распределения в z1 (а затем при необходимости взять модуль полученного значения).
Вот еще один пример:
Рисунок 4 – Определение вероятности попадания результата измерения в определенный диапазон с помощью кумулятивной функции распределения
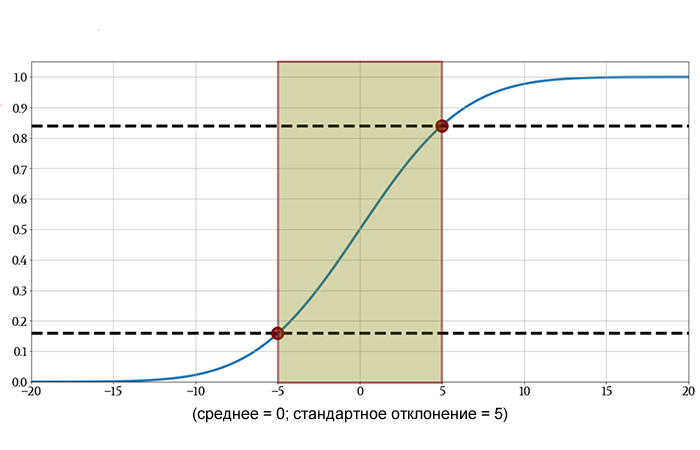
Вероятность того, что результат случайно выбранного измерения будет между –5 и +5, составляет приблизительно (0,84 – 0,16) = 0,68 (или 68%). Более точное значение – 68,27%.
Вероятность и стандартное отклонение
Вы могли заметить, что интервал, выбранный в предыдущем примере, был равен одному стандартному отклонению выше и ниже среднего. Когда мы обсуждаем вероятности со ссылкой на интервалы, представленные в единицах стандартного отклонения, эта информация применяется ко всем наборам данных, которые следуют нормальному распределению. Таким образом, мы можем определить вероятностные характеристики, используя кумулятивную функцию стандартного нормального распределения, а затем распространить эти тенденции на другие наборы данных, просто изменив стандартное отклонение (или размышляя относительно стандартных отклонений).
Выше мы видели, что в нормально распределенных данных измеренное значение имеет шанс 68,27% попасть в диапазон в пределах одного стандартного отклонения от среднего. Мы можем продолжить обобщение нормально распределенных данных следующим образом:
Эти три вероятности дают простое представление того, как будут вести себя нормально распределенные измерения.
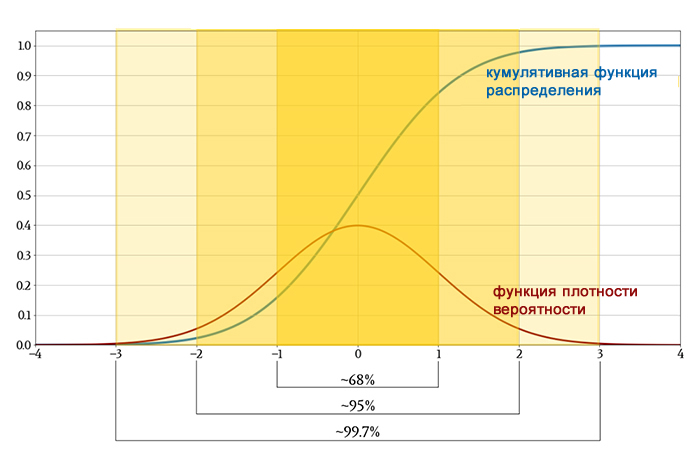
Более приблизительная версия этого обобщения известна как правило 68-95-99,7: если набор данных демонстрирует нормальное распределение, около 68% значений будут в пределах одного стандартного отклонения от среднего, около 95% будут в пределах двух стандартных отклонений, и около 99,7% будут в пределах трех стандартных отклонений.
Рисунок 5 – Демонстрация правила 68-95-99,7 на графиках функции плотности вероятности и функции распределения
Заключение
Мы рассмотрели важный материал, и я надеюсь, что вам понравилось наше исследование нормального распределения и связанных с ним тем статистики. В следующей статье мы рассмотрим два малоизвестных описательных статистических показателя: асимметрию и эксцесс.
Кумулятивная функция распределения
ж ( Икс ) знак равно d F ( Икс ) d Икс <\ Displaystyle е (х) = 
пока существует производная.
Дополнительная кумулятивная функция распределения (хвостовое распределение)
Иногда полезно изучить противоположный вопрос и спросить, как часто случайная величина превышает определенный уровень. Это называется дополнительной кумулятивной функцией распределения ( ccdf ) или просто хвостовым распределением или превышением и определяется как
Свернутое кумулятивное распределение
Функция обратного распределения (функция квантиля)
Некоторые полезные свойства обратного cdf (которые также сохраняются в определении обобщенной обратной функции распределения):
Обратное к cdf можно использовать для перевода результатов, полученных для равномерного распределения, в другие распределения.
Эмпирическая функция распределения
Определение двух случайных величин
Пример совместной кумулятивной функции распределения:
учитывая совместную функцию плотности вероятности в табличной форме, определите совместную кумулятивную функцию распределения.
| Y = 2 | Y = 4 | Y = 6 | Y = 8 | |
| Х = 1 | 0 | 0,1 | 0 | 0,1 |
| Х = 3 | 0 | 0 | 0,2 | 0 |
| Х = 5 | 0,3 | 0 | 0 | 0,15 |
| Х = 7 | 0 | 0 | 0,15 | 0 |