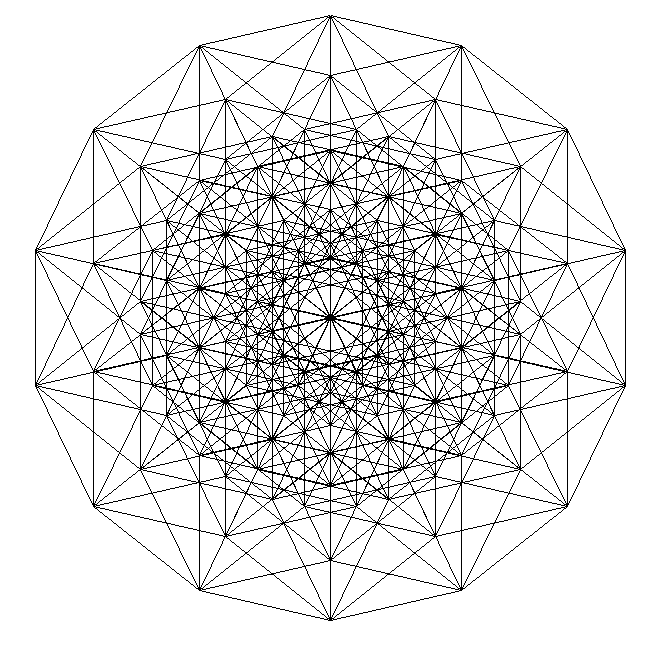
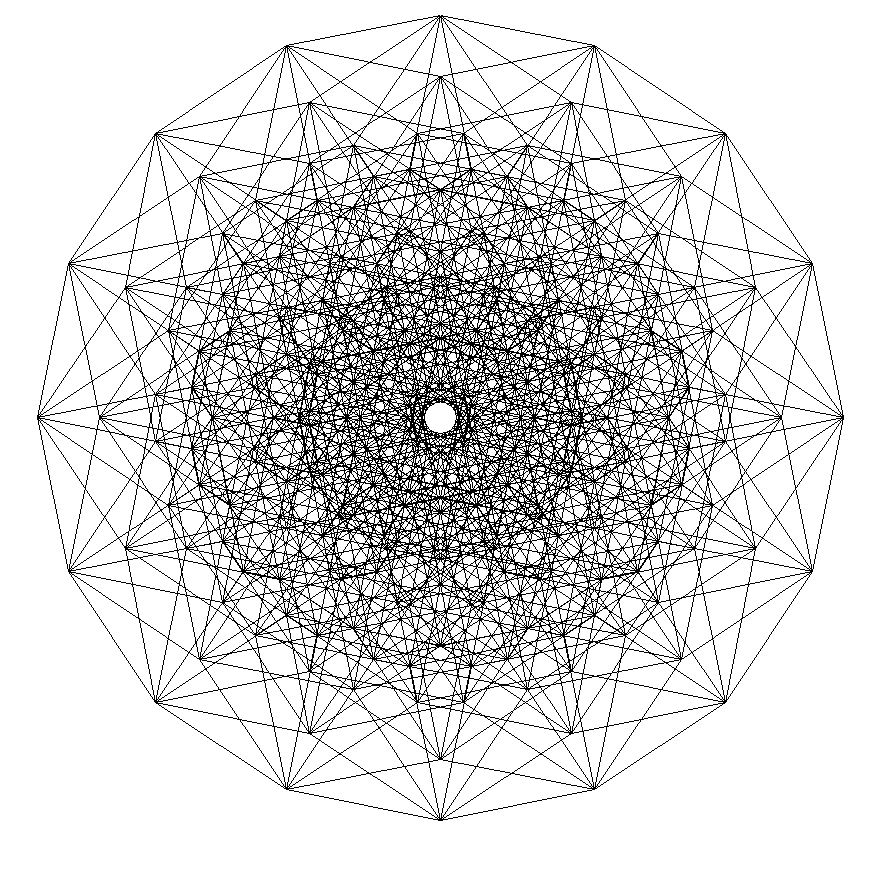
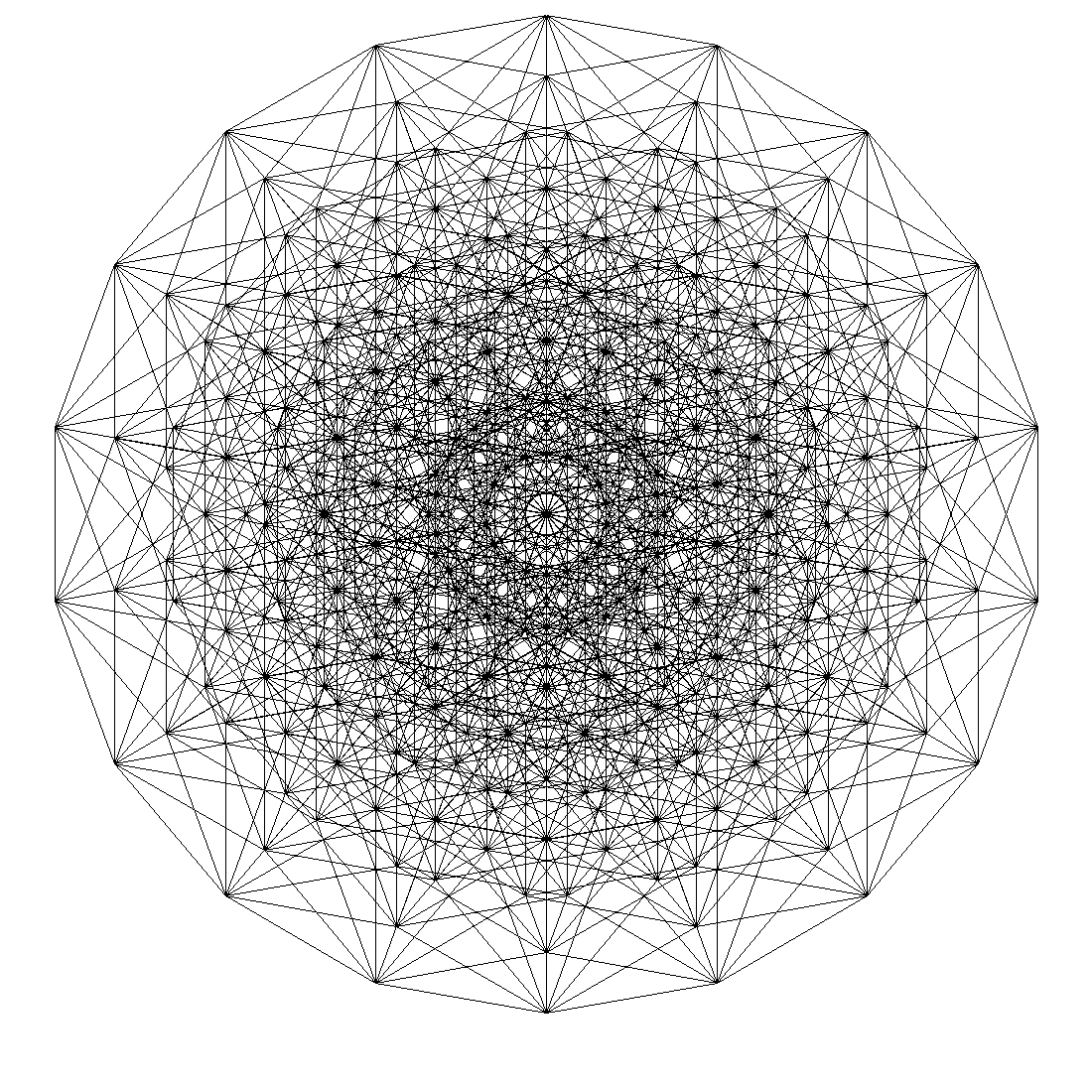
Куб квадрат что дальше

Что такое тессеракт? Четырехмерный объект, который невозможно построить

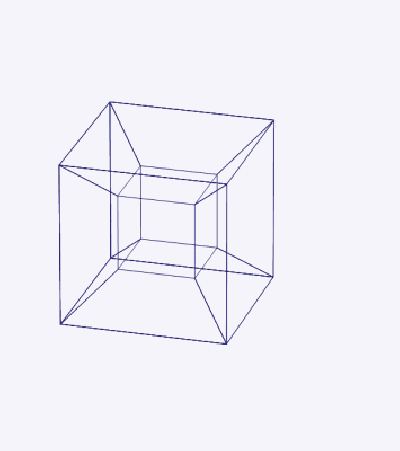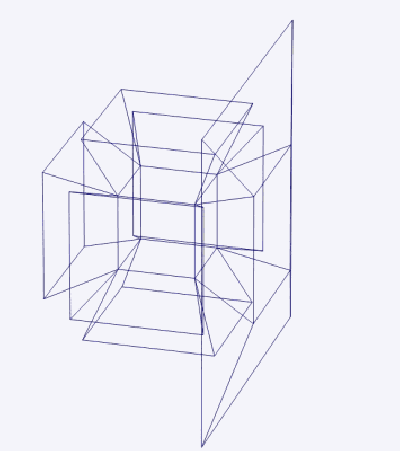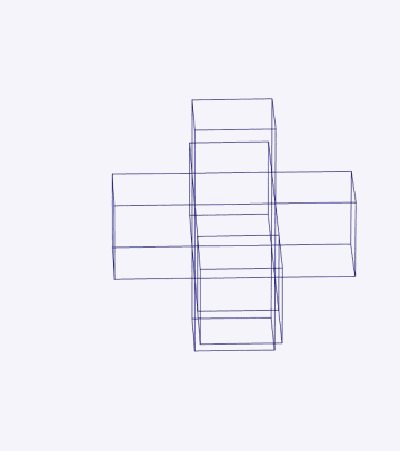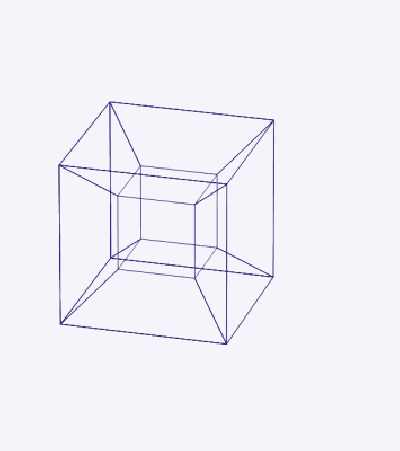
Давайте попробуем понять четвертое измерение. В геометрии четырехмерный аналог куба называется тессерактом. Его легко экстраполировать, рассматривая более низкие измерения.

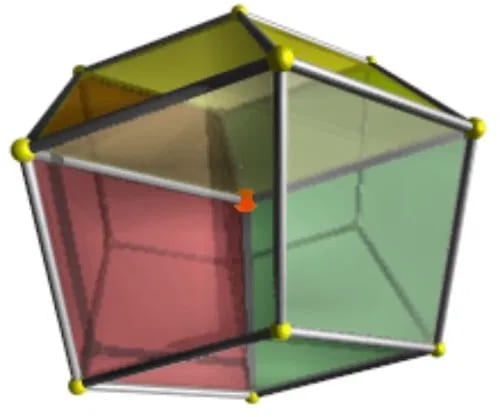
Аналогично, четырехмерный куб (также известный как гиперкуб или тессеракт) имеет 16 вершин. Он может быть создан путем сгущения куба в четвертом измерении. Но поскольку мы живем в трехмерном мире, построить четырехмерный объект невозможно.

В целом можно сказать, что тессеракт относится к кубу так же, как куб относится к квадрату. У него 24 грани, 32 ребра и 16 вершин.

Объект, меняющий размеры, от точки до тессеракта

Тессеракт очень трудно визуализировать

Визуализировать тессеракт или любой другой четырехмерный объект чрезвычайно трудно, если вообще возможно. Это происходит потому, что наше воображение недостаточно сильно, чтобы спроецировать наше сознание в искусственный мир, который сильно отличается от нашего собственного.

Наш мозг устроен так, чтобы преобразовывать двухмерные данные в трехмерное представление. Точнее, наши глаза посылают в мозг пару двухмерных изображений, из которых мозг строит двухмерную+глубинную модель поля зрения.

Это то, о чем наш мозг лучше всего приспособлен думать. Трехмерное пространство легко визуализировать, потому что мы буквально видим его все время. Однако у нас нет прямого опыта более высоких измерений, и поэтому у людей нет четкого прототипа, который можно было бы использовать в качестве трамплина для их визуализации.

С другой стороны, физики и математики, имеющие опыт работы с более высокоразмерными пространствами, более способны, чем остальные, визуализировать их в своем мозгу.

Давайте попробуем визуализировать тессеракт

Как куб можно спроецировать в двухмерное пространство, так и тессеракт можно спроецировать в трехмерное пространство.

Рисунок 2

Поверхность трехмерного куба содержит 6 квадратных граней; аналогично гиперповерхность тессеракта содержит 8 кубических ячеек.

Тессеракт можно развернуть на 8 кубиков в трехмерном пространстве (рис. 2). Это похоже на развертывание куба на 6 квадратов в двумерном пространстве. Разворачивание геометрического объекта [с плоскими сторонами] называется сеткой. В тессеракте 261 сетка.

Существует два типа четырехмерных вращений:

1) Простые вращения: трехмерная проекция Тессеракта (рис. 3), выполняющая простое вращение вокруг плоскости, разделяющей пополам фигуру сверху вниз и спереди слева направо.

Рисунок 3 | Альтернативная проекция тессеракта

2) Двойное вращение: трехмерная проекция тессеракта (рис. 4), показывающая двойное вращение вокруг двух ортогональных плоскостей.

Рисунок 4 | Альтернативная проекция тессеракта

Тессеракт также может быть показан с точки зрения устранения скрытого объема. На рисунке 5, например, красная грань находится ближе всего к четвертому измерению и имеет четыре кубические ячейки, расположенные вокруг нее.

Рисунок 5 | Тессеракт с точки зрения устранения скрытого объема

Тессеракт был открыт в 1888 году

Слово «тессеракт» было придумано британским математиком и писателем-фантастом Чарльзом Говардом Хинтоном. Он впервые использовал это слово в 1888 году в своей книге «Новая эра мышления». Он также придумал несколько новых слов для описания элементов в четвертом измерении.

С тех пор слово «тессеракт» используется в различных видах искусства, архитектуры и научно-фантастических историях (таких, как «Мстители» и «Агенты «Щ.И.Т.»»), где оно не имеет ничего общего с четырехмерным гиперкубом.

Последние исследования

Пространственные представления человека не ограничены трехмерным миром

Группа исследователей из Университета Иллинойса, США, провела исследование, чтобы выяснить, может ли человек развить интуитивное понимание четырехмерного пространства. Для получения точных результатов они использовали виртуальную реальность (VR).

Данные показывают, что люди, не имеющие специальной практики, могут научиться делать пространственные суждения о длине и угле между линейными сегментами, встроенными в четырехмерное пространство, просматриваемое в виртуальной реальности. Их суждение включало данные как трехмерной проекции, так и четвертого измерения. Основные представления были основаны на визуальных образах (установленных алгебраической природы), хотя и примитивных и недолговечных.

Общее число возможных измерений во Вселенной

В то время как общая теория относительности рисует картину четырехмерной Вселенной, теория суперструн утверждает, что она имеет 10 измерений, а расширенная версия, называемая М-теорией, утверждает, что она имеет 11 измерений. В бозонической теории струн пространственное время 26-мерно. Эти теории просто представляют собой математические уравнения. Они настолько сложны, что никто не знает их точной формы.

Эксперимент по изучению теоретических материалов в четырехмерном пространстве

Международная группа исследователей смогла разработать двумерную экспериментальную систему, которая позволяет им анализировать физические свойства «материалов», которые теоретически существуют только в четырехмерном пространстве.

Более конкретно, они продемонстрировали, что четырехмерные квантовые эффекты Холла могут быть эмулированы с помощью фотонов, проходящих через двумерный волноводный массив.

Как эти исследования могут быть полезны в нашем трехмерном мире? Скажем, квазикристаллы (широко используемые для покрытия некоторых антипригарных сковородок), как было показано, имеют скрытые измерения. Этот эксперимент может помочь нам понять физику этого скрытого измерения. Затем эта физика может быть использована в качестве принципа проектирования нового фотонного оборудования.

Источник

Тессеракт и прочие гиперкубы.

Стукнула тут меня мысль нарисовать куб в десятом измерении. Ну точнее проекцию на двухмерный экран. Думал думал думал… Ну теперь когда придумал, все кажется таким простым, но тем не менее думал я напряжно. Да и тему сначала понять надо было.

В общем что такое куб в четвертом измерении.. Будем рассматривать через проекцию на третье.

Начнем с точки. Точка вытягивается в линию Это первое измерение. Линия расползается в квадрат, второе.

Квадрат раздваивается и расходится образуя куб.

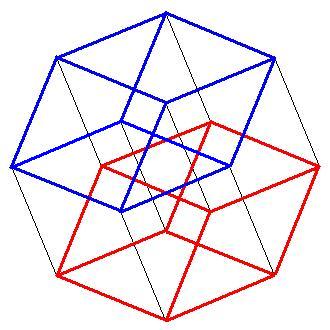
А далее таким же методом вытягиваем куб из куба, и соединяем соответствующие точки.

Вот пример каждая точка красного куба соединена с соответствующей точкой синего.

Тессеракт

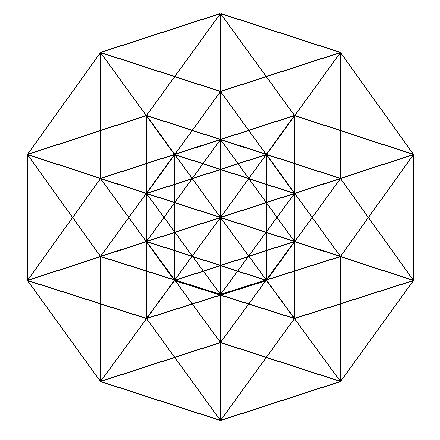
Далее идет пятое (тут я уже не стал возиться с обводкой)

Пентеракт

Хексеракт

Хептеракт

Октеракт

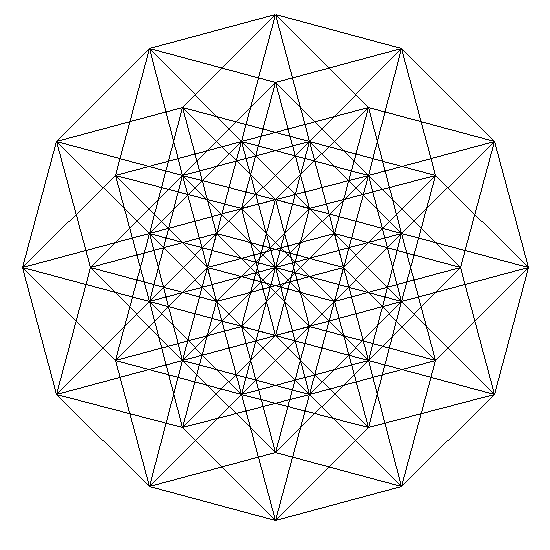
Энтенеракт

И десятимерный куб

Можно конечно и большие размерности и размеры (у меня тут файл 5000х5000 11мерный куб. вес правда всего 3 метра с небольшим) Но это уже если объявится желающий.

Да вот иногда я пишу подобную белеберду вместо кнопок бабло 🙂

54 thoughts on “ Тессеракт и прочие гиперкубы. ”

дружище ты бы к психологу сходил что ли 🙂
тесеракты какие то выдумываешь.

в пол седьмого утра точно бы не пошел, а вот попозжа может и прогулялся бы

Это ж надо было додуматься:) Хотя выглядит красиво, это да…

А на каком языке и с помощью каких библиотек реализовал это? Можно сделать скринсэйвер и выложить в паблик кстати.

На Делфи. рисовал стандартными процедурами на канве.

привет.
почты не нашел, а в аську по пустяку барабанить не хотеxtncz. Есть пару вопросов ричклику — судя по постам, ты с ними работаешь. Как у них с выплатами, задерживают как и сам бегун, или платят исправно как Зорька? Что нужно для аппрува, тупо дор какой-то общетематический в индексе показать, или что?
Заранее благодарен, пост можешь тереть, а ответить на почту, если не тяжело, ибо у тебя нет подписки)

Платят нормально.
Даты последних 8 платежей
20.10.2009
05.10.2009
17.09.2009
04.09.2009
19.08.2009
20.07.2009
25.06.2009
05.06.2009

Для апрува аккаунта надо показать свою вменяемость и адекватность.

Да, меня пример дора попросили показать. Спросили о трафике, о опыте, о том на каких форумах зареган и какова активность.
Уников на момент регистрации имел только 200 вместо 2к.

(Продублировал на почту)

Даже обычный гиперкуб 4-х мерный изобразить на плоскости невозможно, видел где-то в виде анимации, но все равно не то:) А то что вы изобразили это получается как бы тень от металлического каркаса таких фигур.

Я тоже видел анимацию.

Изобразить на плоскости объект большей мерности конечно невозможно. Не возможно изобразить даже обычный трехмерный куб. Поэтому изображение куба называется проекцией на плоскость.

о чем я и написал в посте словами «Ну точнее проекцию на двухмерный экран.»

Более того когда ты сказал «тень от металлического каркаса» ты сделал проекцию на трехмерность, то есть упростил гиперкуб в этот самый металлический каркас.

Так и я упростил всё до плоского изображения.

Хотя если совсем точно то тут изображенны проекции на плоскость трехмерных изображений, которые получены путем проекции гиперкубов в трехмерность.

Выложи программку что ли 🙂 с исходниками

Да какие исходники.. я программированию не обучен, поэтому думаю любого человека код введет в ступор.

На крайний случай я могу описать алгоритмы в отдельном посте. В конце концов именно в алгоритмах 90% сложности этой программы.

вот это офигеть. жги еще. на самом деле. вот у меня вопрос такой: ты можешь представить это все свое творчество в объеме? просто у меня например с этим всегда были траблы.. начиная с 4-го измерения, 3-х мерное пространство — 3 взаимно-перпендикулярных координатных оси, 4-х мерное пространство 4 оси. Куда ее пристроить-то? Ты я смотрю просто берешь и смещаешь трехмерный куб в разных направлениях, т.е каждая последующая мерность — реализуется виде некоторого движения. Это здорово, но все таки не то. В итоге получаешь просто траекторию движения точек куба, чем больше направлений смещения берешь,тем больше размерность. Однако, навряд ли это именно то, что происходит в действительности. Напиши, что думаешь по этому поводу.

Виноват. Вот перечитал пост свой. Все верно. Натупил слегка. Не о том подумал.

По факту это все проекции на третье измерение.

Думаю представить четвертое геометрическое пространство можно только абстрактно, но не визуально. Так как визуально все упирается в 2 и 3 мерность.

И даже если вспомнить разбитие на плоскости как это было в черчении, то трехмерный объект это просто три плоскости. А четырехмерный значит 4 объемности. (Смотря с каждой из четырех мерностей мы будем видеть трехмерный объект) формально четырехмерный объект будет описан, но чтобы представить его нужно иметь другой мозг.

И каждое новое смещение можно рассматривать как представление новой грани.. То есть мы копируем объект придавая ему еще одну глубину, будто бы мы посмотрели на объект с такого ракурса где видна новая ось. Но эти новые грани будут изначально трехмерными проекциями.
Если отойти от условностей и сделать многомерный куб в третьем измерении, то это будет тот же самые трехмерный куб, потому что для человеческого мозга не существует 4 геометрического измерения… Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.

Можно представить четвертое измерение как плоский срез пространства, имеющий глубину. Но это опять же проекция третьего измерения, где глубину третьего измерения подменяют глубиной четвертого.

Я вообще как то заморочился с перелинковкой сетки сателлитов в 400 штук такою штуку навоял парни долго потом всматривались в итоге сказали что надо лечиться,сейчас эта перелинковка цветет и процветает.
Извини за офтоп!!Но твои фигуры просто мне напомнили это!

Автор? ты что фентези перечитал? ил переиграл малость?

Отвечу на вопросы по очереди.
Автор
Перечитал
Переиграл
🙂

Мне думается что тесеракт- это просто невозможная фигура, как например треугольник из брусков у которого все углы по 90 градусов, просто интересная безделушка. А 4-ое измерение это из научной фантастики, одни лишь теории.

Да фигура невозможная, потому что человек не способен воспринимать 4 геометрическое измерение.

По повожу фантастики.
Когда программисты задают массив, они вполне могут сделать его четырех, пяти и более мерным.

Поэтому надо четко понимать о каком измерении идет речь. В широком смысле под четвертым измерением понимают время.
В узком геометрическом это просто дополнительная «глубина», которую человек не способен воспринять, и поэтому бОльшие мерности представляются проекциями на третье.
Поэтому, да. большие геометрические мерности существуют только теоретически.

«Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.»
А мне почему-то кажется, что если бы человек из плоскости смотрел на куб, то он видел бы его лишь как линию. Он мог бы понять, что это квадрат(не куб, заметьте, для двумерного человека понятие куб абстрактное, как для нас трёхмерных абстрактным является тессеракт) лишь в том случае, если бы ходил вокруг этого квадрата, изменение скорости удлиннения/укорачивания видимой линии служило бы показателем того, что там есть угол.

третье измерение глубина.
На плоскости мы будем видеть ширину и высоту, достаточно чтобы построить квадрат.

Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.

И мне кажется обсуждение ушло куда то не туда.
Еще раз повторюсь это просто геометричекие проекции.

Я имею ввиду, что он живёт на плоскости, понятий «верх\низ» просто нет, как двумерный человек может посмотреть на плоскость сверху? Ведь «сверху» для него является третьим(гипотетическим) измерением. =))

если нет высоты то, тогда есть ширина и глубина. В любом случае есть два измерения а их достаточно для квадрата, на то она и плоскость.

Меня видимо поразило внезапное косноязычие, если я так долго не могу донести свою мысль… Представьте, что вы двумерный человек живущий на плоскости, посмотрите его глазами, как вы выберетесь в третье измерение(посмотрите сверху на плоскость, которая имеет длину и ширину)? Я прекрасно понимаю, что плоскости достаточно чтобы построить квадрат. А вот чтобы его увидеть нужно ещё одно измерение.
«…если бы человек из плоскости смотрел на куб, то он видел бы его лишь как линию. Он мог бы ПОНЯТЬ, что это квадрат», НО не смог бы увидеть.

Так же как и мы видим плоские объекты а не объемные. Но без всяких проблем рассуждаем о объеме.

И разве это
«Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.» я не о том же самом говорил?

Поэтому я и говорил о высоте. он же своими глазами не только вперед-назад смотрит, но и вверх-вниз

тем не менее Penteract и Septeract существуют в виде матеиатических констант.

всё же, нарисовать 4х мерный объект в 3х мерном виде и поместить на 2х мерный экран, всё равно мы увидим не то, даже если предположить существование четвертого измрения

Вы всерьез думаете, что я не видел те картинки?
Мои картинки имеют равные грани, те — нет. Приглядитесь.

класс. молодец. а то народ совсем тупой

Уважаемый Elsper! (Извините, не знаю как правильно к Вам обратиться).
Я безмерно рада, увидев Ваши чертежи. Вы чертите ГОРИЗОНТАЛЬНЫЕ проекции трёхмерных проекций многомерных гиперкубов. И эти трёхмерные проекции многомерных гиперкубов (любых измерений!) можно чертить и во фронтальной, профильной проекциях, и в абсолютно в любых ракурсах. Более того, с помощью трубочек и лески я легко создала сами трёхмерные проекции четырёхмерного, пятимерного и шестимерного гиперкубов, на семимерный у меня не хватает трубочек.
Я написала работу «»Начала» геометрии многомерных измерений», в которой мною выявлен и подробно описан «Универсальный метод построения (черчения) трёхмерных проекций гиперкубов любых n-мерных измерений (3ПГК-n) в любых проекциях и ракурсах». Моя работа — это рукопись, правда, отсканированная, — потому что во время написания моих работ у меня не было компьютера, более того, я и сейчас, имея компьютер, не могу толком научиться чертить чертежи на компьютере — старая я, мне 64 года.
Уважаемый Elsper! Если Вам интересно прочитать или хотя бы просмотреть мою работу (где, кстати, я начертила горизонтальную проекцию трёхмерной проекции ДВЕНАДЦАТИМЕРНОГО гиперкуба), пожалуйста, сообщите мне свой электронный адрес, и я с радостью вышлю Вам свою работу.
С уважением,
Михайлова Людмила Михайловна.

Здравствуйте Людмила Михайловна.
Идея начертания гиперкубов была для меня просто тренировкой для мозгов. Я возвращался к ней еще два раза http://elsper.ru/stereokartinki-giperkuby-stereo-giperkuby/ и http://elsper.ru/2011/02/giperkuby-2/, но за три года уже почти утратил к ней интерес.

К тому же, так как я не рисовал их, а программировал, то мне тоже было нужно разработать универсальный метод построения, с чем я справился. И даже если бы не справился, то все равно думал бы сам, потому, что именно в этом и заключается смысл тренировки. В том, чтобы решить задачу самостоятельно.

Однако, если хотите, я могу сделать ссылку на вашу работу. Интересующиеся смогут ее скачать и прочитать.
Кроме того, вы упомянули трехмерные проекции. Если у вас есть фотографии, то их тоже можно опубликовать. Думаю они заинтересуют всех, кто сюда заходит.
Хотите так?

Здравствуйте, уважаемый Elsper!
Мне очень больно и стыдно признаваться в своей тупости: год назад я купила компьютер, научилась только пользоваться электронной почтой и выходить в интернет, я не могу писать на компьютере математические знаки, формулы, строить таблицы и чертить чертежи — старая я.
До 2011 года я жила в Туркмении. Там же написала свои работы по математике — карандашом, на бумаге, потом эти листы сканировались (т.е. хоть как-то приведены в электронный вид) — это всё, что я могла сделать там, в Туркмении.
С 2011 года я живу на Украине в г.Ивано-Франковске. В квартире я совершенно одна и мне совершенно некому помочь в освоении работы на компьютере.
Вот когда я пишу письмо в своей электронной почте, там на странице есть знак «Прикрепить файл», и я прикрепляю свои работы, — это мне показали. А как вот сейчас, в этом письме, прикрепить свою работу — я не знаю.

Я очень рада: рыская по интернету, я пока увидела — Вы единственный, кто вплотную смог приблизиться к построению горизонтальных проекций трёхмерных проекций n-мерных гиперкубов! Но Ваши проекции правильны только в тех случаях, где n-мерность НЕЧЁТНАЯ. Например, посмотрите на свой ОКТЕРАКТ (восьмое измерение) — в центре чертежа образовался «кружок пустоты», а в данной проекции октеракта центральная точка на чертеже совмещает 16 вершин.
Слава Богу, научили меня пользоваться скайпом. Вот по скайпу я могу показать Вам свои модели трёхмерных проекций четырёхмерного, пятимерного и шестимерного гиперкубов. Если Вы напишете на мою электронную почту свой электронный адрес, то я сообщу Вам свой «логин» для скайпа.
Конечно, я очень хотела бы, чтобы мои работы были хоть как-то опубликованы (для кого я их писала? — для людей!), но я не знаю как это сделать.

Спасибо, что ответили. Всего Вам самого доброго.
С уважением,
Михайлова Людмила Михайловна.

Программа начального многомерного геометрического моделирования NDL_4D
neoethics.narod.ru/n/neo_school/NDL_4D/index.html

Разработка возникла во многом благодаря и Вашей, Elsper, тематической компиляции, за что особое Вам большое спасибо. :)))

Возможно, в случае знакомства, возникнут мобильные конструктивы по дальнейшему развитию идеи освоения многомерных пространства — искренне будем благодарны за любые интересные мысли в данном направлении.

С уважением, Stellari.stA.G

Приятно, что мои работы служат не только мне. )
Правда сейчас меня интересуют совсем другие вопросы.

Источник

Степень числа. Квадрат и куб числа

Содержание

Мы уже узнали, что записать сумму, в которой все слагаемые равны друг другу, можно в виде произведения. Например, если у нас есть выражение:

Но можем ли мы сделать короче выражение, в котором произведение имеет равные друг другу множители? Ответ прост – можем! Если в случае со сложением чисел, где все слагаемые одинаковые, мы получим произведение, то при умножении равных друг другу чисел, мы получим степень числа. Давайте разберем поподробнее, чем же является степень и как решать выражения со степенями.

Понятие степени

У каждого степенного выражения есть свое основание и свой показатель. Давайте рассмотрим на примере:

Квадрат и куб числа

Для удобства запоминания квадратов чисел существуют специальные таблицы квадратов первых 10 натуральных чисел:

Для запоминания кубов чисел также есть специальные таблицы кубов первых 10 натуральных чисел:

Первую степень числа считают равной самому числу.

Решение задач

Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.

Источник

Урок 25 Бесплатно Степень числа. Квадрат и куб числа

На данном уроке мы познакомимся с понятием степени числа.

Выясним, что называют «показателем степени» и «основанием степени».

Научимся вычислять квадрат и куб числа.

Составим таблицу степеней первых десяти натуральных чисел и рассмотрим ряд задач с использованием таких таблиц.

Определим, в каком порядке выполняют действия в выражениях, содержащих степень.

Степень числа

Известно, что сумму равных слагаемых можно заменить произведением.

Например, сумму пяти слагаемых, каждое из которых равняется четырем, можно записать короче:

4 + 4 + 4 + 4 + 4 = 5 ∙ 4

В произведении число 5 указывает на количество одинаковых слагаемых.

В свою очередь произведение одинаковых множителей тоже можно записать компактнее.

Произведение n одинаковых множителей можно представить в виде степени.

В буквенном виде произведение равных множителей можно представить следующим образом:

а— любое натуральное число.

Читают «а в n-ной степени» или «а в степени n».

Число а называют основанием (число, возводимое в степень).

n— это показатель степени (число, которое указывает сколько раз повторяется основание степени).

Степень числа представляют всегда так: записывают основание степени, а показатель ее записывают меньше размером в верхнем правом углу основания степени.

Операция умножения одинаковых множителей называется возведением в степень.

Например, произведение пяти множителей, каждое из которых равняется четырем, можно записать так:

4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4 5

Читают данную запись следующим образом:

4 5 — четыре в пятой степени.

Данная степень равна произведению трех двоек.

2— основание степени.

3— показатель степени.

Данная степень равна произведению четырех пятерок.

5— основание степени.

4— показатель степени.

Пройти тест и получить оценку можно после входа или регистрации

Квадрат и куб числа

Вторую степень числа называют квадратом числа.

Так, квадрат любого натурального числа а будет представлять собой произведение двух одинаковых множителей: а ∙ а = а 2 (говорят и читают «а в квадрате»).

2 2 (два во второй степени) иначе говорят и читают «два в квадрате».

10 2 (десять во второй степени) иначе говорят и читают «десять в квадрате».

27 2 (двадцать семь во второй степени) иначе говорят и читают «двадцать семь в квадрате».

Давайте сосчитаем квадраты первого десятка натуральных чисел (возведем во вторую степень первые десять натуральных чисел), используя таблицу умножения.

Один в квадрате равняется одному: 1 2 = 1 ∙ 1 = 1.

Два в квадрате равняется четырем: 2 2 = 2 ∙ 2 = 4.

Три в квадрате равняется девяти: 3 2 = 3 ∙ 3 = 9.

Четыре в квадрате равняется шестнадцати: 4 2 = 4 ∙ 4 = 16.

Пять в квадрате равняется двадцати пяти: 5 2 = 5 ∙ 5 = 25.

Шесть в квадрате равняется тридцати шести: 6 2 = 6 ∙ 6 = 36.

Семь в квадрате равняется сорока девяти: 7 2 = 7 ∙ 7 = 49.

Восемь в квадрате равняется шестидесяти четырем: 8 2 = 8 ∙ 8 = 64.

Девять в квадрате равняется восьмидесяти одному: 9 2 = 9 ∙ 9 = 81.

Десять в квадрате равняется сотне: 10 2 = 10 ∙ 10 = 100.

Оформим полученные данные квадратов натуральных чисел от 1 до 10 в виде таблицы.

Таблица квадратов первых десяти натуральных чисел

Учитывая данные таблицы квадратов, решим уравнение.

Решим уравнение х 2 = 49.

Решить уравнение- это значит найти корень уравнения (в нашем случае установить значение х).

Следовательно, корень уравнения (х) равен семи.

х 2 = 49

х = 7

Проверка: подставим найденное значение неизвестной (х = 7) в исходное уравнение х 2 = 49, получим:

7 2 = 49

7 ∙ 7 = 49

49 = 49

Ответ: х = 7.

У меня есть дополнительная информация к этой части урока!

Чтобы возвести в любую степень число 10, необходимо дописать после единицы нули, количество которых показывает показатель степени.

Разберем пример первый.

Найдите четвертую степень десяти (десять в четвертой степени 10 4 ).

10— это основание.

4— это показатель степени.

Так как по вышеизложенному правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:

10 4 = 1 0000

На самом деле, если перемножить (по определению степени) четыре десятки, то получим:

10 4 = 1 0 ∙ 1 0 ∙ 1 0 ∙ 1 0 = 1 0000

Пример второй: найдите третью степень десяти (десять в третьей степени 10 3 ).

10— это основание.

3— это показатель степени.

Так как по правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:

10 3 = 1 000

Соответственно, если перемножить (по определению степени) три десятки, то получим:

10 3 = 1 0 ∙ 1 0 ∙ 1 0 = 1 000

Рассмотрим обратную ситуацию:

Представим число 100 в виде степени с основанием 10.

Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (1 00 ).

Число 100 содержит два нуля, следовательно, это число в виде степени с основанием 10 представим следующим образом:

1 00 = 10 2

10— это основание.

2— это показатель степени.

Рассмотрим еще один подобный пример.

Представим число 10000 в виде степени с основанием 10.

Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (1 0000 ).

Данное число содержит четыре нуля, следовательно, 10000 в виде степени с основанием 10 представим следующим образом:

1 0000 = 10 4

10— это основание.

4— это показатель степени

Третья степень числа тоже имеет свое название.

Число в третьей степени называют кубом числа.

Так, куб любого натурального числа а будет представлять собой произведение трех одинаковых множителей: а ∙ а ∙ а = а 3 (говорят и читают «а в кубе»).

2 3 (два в третьей степени) иначе говорят и читают «два в кубе».

10 3 (десять в третьей степени) иначе говорят и читают «десять в кубе».

27 3 (двадцать семь в третьей степени) иначе говорят и читают «двадцать семь в кубе».

Давайте определим кубы первого десятка натуральных чисел (возведем в третью степень первые десять натуральных чисел), используя таблицу умножения.

Один в кубе: 1 3 = 1 ∙ 1 ∙ 1 = 1.

Два в кубе: 2 3 = 2 ∙ 2 ∙ 2 = 8.

Три в кубе: 3 3 = 3 ∙ 3 ∙ 3 = 27.

Четыре в кубе: 4 3 = 4 ∙ 4 ∙ 4 = 64.

Пять в кубе: 5 3 = 5 ∙ 5 ∙ 5 = 125.

Шесть в кубе: 6 3 = 6 ∙ 6 ∙ 6 = 216.

Семь в кубе: 7 3 = 7 ∙ 7 ∙ 7 = 343.

Восемь в кубе: 8 3 = 8 ∙ 8 ∙ 8 = 512.

Девять в кубе: 9 3 = 9 ∙ 9 ∙ 9 = 729.

Десять в кубе: 10 3 = 10 ∙ 10 ∙ 10 = 1000.

Оформим полученные данные кубов натуральных чисел от 1 до 10 в виде таблицы.

Таблица кубов первых десяти натуральных чисел

1000

С помощью таблицы кубов можно легко и просто решать примеры и задачи, в которых необходимо высчитывать третью степень числа.

Представим в виде куба число 343.

По таблице кубов видим, что 343 = 7 3

Проверим: найдем произведение трех семерок:

7 3 = 7 ∙ 7 ∙ 7 = 49 ∙ 7 = 343

На прошлом уроке мы подробно разобрали порядок выполнения арифметических действий в выражениях.

Выяснили, что в первую очередь выполняются арифметические действия в скобках, затем-действия второй ступени (умножение и деление) по порядку их следования слева направо, и только потом выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.

Однако, в математических выражениях, в которых отсутствуют скобки, но есть действия первой, второй ступени и степень, возведение в степень выполняется раньше других действий, только потом умножают, делят, складывают и вычитают в установленном правилами порядке.

Если в скобках содержится степенное выражение, то действия в скобках выполняются по порядку слева направо, начиная с действий высшей ступени- возведение в степень, и далее по известным нам правилам.

За скобками действия выполняют, соблюдая порядок выполнения действий без скобок, рассмотренный выше.

Рассмотрим поясняющие примеры.

При решении различных задач и примеров будем пользоваться составленными таблицами степеней.

Пример 1.

Определим порядок действий в выражении и найдем его значение.

Так как исходное выражение не содержит скобки, а возведение в степень- это действие более высокой ступени, чем умножение, деление, сложение и вычитание, следовательно, в первую очередь необходимо выполнить вычисление степени, затем слева направо в порядке следования сначала действия второй ступени (деление), затем- действия первой ступени (вычитание).

1) 8 2 = 8 ∙ 8 = 64 (по определению степени или по таблице квадратов).

2) 64 ÷ 4 = 16

Пример 2.

Найдем значение данного выражения, определив порядок действий в нем.

Согласно порядка выполнения действий сначала выполняются действия в скобках.

Найдем разность 21 и 11.

Далее выполняется действие высшей ступени (возведение в степень), т.е. разность, полученную в скобках, возведем в квадрат.

Найдем, чему равно 10 2 по определению степени или по таблице квадратов.

2) 10 2 = 10 ∙ 10 = 100

Затем выполним действия, которые находятся в исходном выражении за скобками.

Определим третью степень двойки по таблице кубов или по определению степеней.

3) 2 3 = 2 ∙ 2 ∙ 2 = 8

4) 100 ∙ 8 = 800

У меня есть дополнительная информация к этой части урока!

С давних пор основными арифметическими операциями являются операции сложения, вычитания, умножения и деления.

Представление о степени, как об отдельной операции возникло не сразу.

Однако степени применялись при вычислении площадей и объемов уже у древних народов: степень числа высчитывали при решении различных задач в Древнем Египте, Древней Греции, в Вавилоне.

Диофант Александрийский древнегреческий математик, философ (III век н.э.) в своем знаменитом труде «Арифметика» описал первые натуральные степени чисел.

Диофант первым из античных ученых предложил специальные обозначения для шести степеней неизвестного (квадрат, куб, квадрато-квадраты, квадрато-кубы и т.д.)

Древнегреческий ученый Пифагор и его последователи (пифагорейцы) проявляли большой интерес к числам, искали в них скрытый смысл, закономерности и приписывали им различные свойства.

Пифагорейцы предполагали, что каждое число можно представить в виде фигуры.

Так, например, числа 4, 9, 16, 25 они представляли в виде квадратов.

В Древнем Вавилоне для вычисления и расчетов был создан целый ряд вычислительных таблиц: таблицы умножения, таблицы квадратов и кубов и многие другие.

В Древней Индии успешно развивалась наука.

Высоких результатов индийцы добились в астрономии, медицине, математике.

Индийские ученые часто оперировали большими числами.

В Древней Индии существовало понятие степени числа, математики того времени умели вычислять площади и объемы фигур, разработали алгоритмы вычисления всех арифметических операций, в том числе определение степени числа.

Важнейшим открытием индийских ученых в математике стало изобретение позиционной системы счисления, а также запись (чтение) чисел, для каждой цифры был придуман свой знак.

Математические труды их были изложены в основном в словесной форме на древнеиндийском языке в священных писаниях, книгах, сказаниях.

Потребность в решении более сложных математических задач со степенями заставляла ученых разных стран расширять понятие о степени, систематизировать и обобщать известные уже данные о ней.

В начале XV века самаркандский математик Гияс ад-Дин Джемшид Аль-Каши рассматривал нулевой показатель степени, в это же время французский ученый Никола Шюке применял в своих трудах нулевой и отрицательный показатель степени.

В 1544 г. немецкий математик Михаэль Штифель в своей книге «Полная арифметика» впервые ввел понятие «Показатель степени».

Постепенно понятие степени становится все шире, оно применяется не только к числу, но и к переменной.

Математики средневековья пытались установить единое обозначение степени и сделать ее компактней.

Французский ученый математик Франсуа Виет ввел буквенное обозначение (N, Q, C) для первой, второй и третьей степени.

Нидерландский математик Симон Стевин предложил называть степень по их показателям, отвергая тем самым словесные обозначения степеней, составленные Диофантом.

Современное обозначение степеней (а n ), где а-основание степени, n-показатель степени, ввел французский математик Рене Декарт.

Пройти тест и получить оценку можно после входа или регистрации

Источник