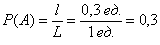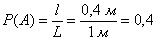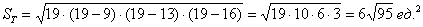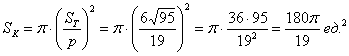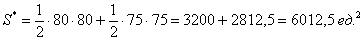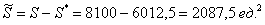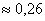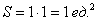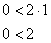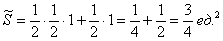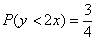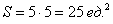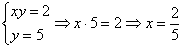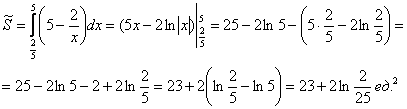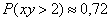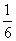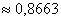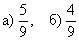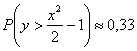Круг вписан в квадрат найти вероятность того что случайная точка

19.07.202219.07.2022 admin 0 Comments

Найдите вероятность попадания случайной точки внутрь круга, вписанного в квадрат

Написать условие попадания координат точки (x, y) строго внутрь круга радиуса 1
Написать условие попадания координат точки (x,y) строго внутрь круга радиуса 1. в программе на.

Найдите вероятность того, что точка попадет внутрь куба, вписанного в шар
В шар наудачу брошена точка. Найдите вероятность того, что точка попадет внутрь куба, вписанного в.

Найдите параметры А и В и вероятность попадания этой случайной величины в интервал
Доброго времени суток, форумчане!! Не могли бы вы помочь в решении 4ех задача или нескольких из.

Решение

Правильный ответ вам mathmichel уже написал:
А что касается вашего вопроса, как делать, то вероятность равна:

P = площадь круга / площадь квадрата

сторона квадрата a = 1
Площадь квадрата = a^2 = 1^2 = 1

Если круг вписан в квадрат, то диаметр круга равен стороне квадрата, соответственно радиус круга r = 1/2
Площадь круга = pi*r^2 = pi*(1/2)^2 = pi/4

Найти вероятность попадания точки в часть круга
Внутрь круга с цетром в точке (0,0) и радиусом 1 наудачу выбирается точка P (x,y). Найти.

Найдите вероятность попадания точки в незаштрихованную фигуру
Точка бросается наугад в круг радиуса 1. Найдите вероятность попадания точки в незаштрихованную.

Нахождение площади круга вписанного в квадрат со стороной 4 см
Здравствуйте помогите сделать программку для нахождение площади круга вписанного в квадрат со.

Источник

Геометрическое определение вероятности. Задачи с решениями

За окном ранние осенние деньки, и жёлтая листва на деревьях навевает лирическое и немного грустное настроение…. Но впереди ещё целый учебный год и в такие моменты нужно обязательно настроиться на плодотворную работу! Спешу обрадовать всех хандрящих читателей своим фирменным рецептом, позволяющим быстро повысить тонус своего организма. Для этого достаточно немножко вспомнить геометрию… …нет, я согласен, что иногда она усыпляет, но в небольших дозах – исключительно бодрит! И, главное, очень действенно – как только начинаешь принимать живительные порции знаний, так сразу никакой сезонной депрессии!

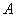
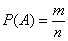
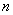
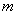
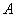
Ещё на первом уроке по теме мы познакомились с классическим определением вероятности появления некоторого события в испытании и простейшей формулой , где – общее число всех возможных равновозможных, элементарных исходов данного испытания, а – кол-во элементарных исходов, благоприятствующих событию .

Возникли затруднения с терминологией и/или пониманием? Пожалуйста, начните с основ теории вероятностей.

Едем дальше: классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом недостатков. Даже правильнее сказать, не недостатков, а ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:

На отрезок 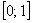наудачу бросается ~~голодная~~ точка. Какова вероятность того, что она попадёт в промежуток ?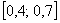

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу 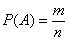(ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности.

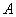
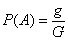
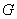
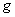
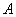
Всё очень похоже: вероятность наступления некоторого события в испытании равна отношению , где – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а – мера, выражающая количество благоприятствующих событию исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.

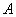
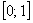
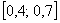
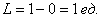
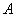
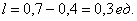
Рассмотрим событие: – брошенная на отрезок точка, попала в промежуток . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: , а благоприятствующие событию исходы – длиной вложенного отрезка: По геометрическому определению вероятности:

Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:

Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.

Решение: «чего тут сложного? Вероятность равна 1/5-й». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать не более 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого: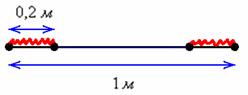

Рассмотрим событие: 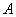– длина обрезка составит не менее 0,8 м.

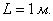
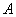
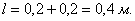
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: Благоприятствующие событию участки разреза отмечены на рисунке красным цветом и их суммарная длина равна: По геометрическому определению:

Ответ: 0,4

Какой можно сделать вывод? Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ. Импульсивность вообще штука скверная – это ошибки, ненужные покупки, испорченные ~~кожные покровы~~ отношения и т.д.… но не будем о грустном!

При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры: 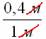, в результате чего получилась привычная безразмерная вероятность.

Разминочная задача из сборника Рябушко:

После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?

Краткое и решение и ответ в конце урока.

Значительно чаще встречаются примеры, в которых фигурируют площади:

В треугольник со сторонами 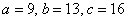вписан круг. Точка произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.

Напоминаю, что вписанный круг лежит внутри треугольника и касается его сторон в 3 точках

Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга. Что тут сказать? Ищем площади:

Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона: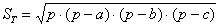
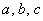
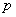
, где – длины сторон треугольника, а – полупериметр.

Сначала вычислим полупериметр треугольника: 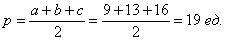, а затем его площадь:

Методику вынесения множителей из-под корня я освещал ещё в древние-древние времена на вводном уроке по аналитической геометрии.

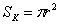
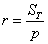
Площадь вписанного круга найдём по формуле , где – его радиус.

Откуда брать геометрические формулы? Нужные формулы можно найти в школьном учебнике или другом источнике информации. При этом нет никакой необходимости специально их разучивать, лично я вспомнил только 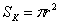, а всё остальное в считанные минуты нашёл в Википедии. И через считанные минуты всё это благополучно забуду =)

Итак, площадь вписанного круга:

По геометрическому определению:
– вероятность того, что точка попадёт во вписанный круг.

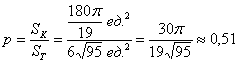
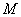
Ответ:

Более простой пример для самостоятельного решения:

В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.

Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!

А теперь рассмотрим широко известную задачу о встрече:

Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?

Давайте немного осмыслим условие. Во-первых, автомобили могут подойти на погрузку в любом порядке, а во-вторых – в любые моменты времени в течение полутора часов. По первой оглядке решение представляется довольно трудным. И для неподготовленного человека оно действительно окажется «не по зубам». Подробный анализ метода решения этой задачи можно найти, например, в учебном пособии Гмурмана, я же ограничусь в известной степени формальным алгоритмом:

Решение: сначала выясняем длительность временнОго промежутка, на котором может состояться встреча. В данном случае, как уже отмечено выше, это полтора часа или 90 минут. При этом здесь не имеют особого значения фактические временнЫе рамки – погрузка автомобилей, может состояться, например, утром с 8.30 до 10.00, и решение будет точно таким же.

Вычисления допустимо проводить как в долях часа, так и в минутах. На мой взгляд, в большинстве случаев удобнее работать с минутами – меньше путаницы.

На первом шаге изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц; при этом одна из вершин квадрата совпадает с началом координат, а его смежные стороны лежат на координатных осях.

Общему множеству исходов будет соответствовать площадь данного квадрата: 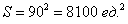Размерность лучше указать в квадратных единицах, поскольку квадратные минуты смотрятся как-то неудачно.

Далее по оси от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение):

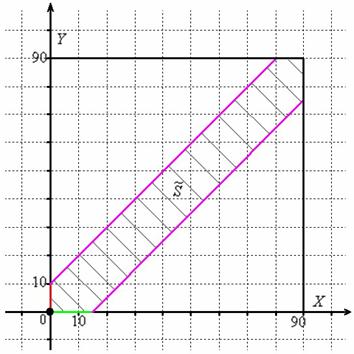
Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).

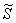
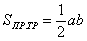
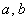
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще найти площади двух прямоугольных треугольников с помощью формулы , где – длины катетов. Обратите внимание, что в общем случае эти треугольники не равны. У нас: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Таким образом, суммарная площадь треугольников составляет:

И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:

По геометрическому определению:
– вероятность того, что одной машине придется ждать окончания погрузки другой.

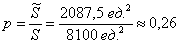
Ответ:

Если в разобранной задаче встреча была явно нежелательна, то в следующей – скорее, наоборот =) Романтичный эпизод для самостоятельного изучения:

Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.

Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! …прошу прощения за тонкий юмор =) Решение, чертёж и ответ в конце урока.

Оставшиеся примеры статьи посвящены не менее распространённой задаче на геометрическое определение вероятности. Для начала заманивающий пример:

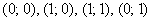
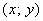
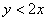
В квадрат с вершинами наудачу брошена точка . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.

Решение: изобразим на чертеже искомый квадрат и прямую :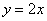

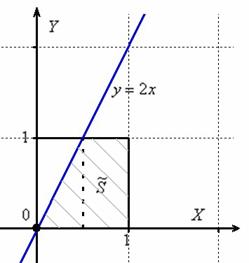
Общему множеству исходов соответствует площадь квадрата

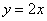
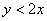
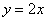
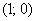
Прямая делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой , например, точку и подставить её координаты в неравенство:

Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь 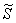трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника:

По геометрическому определению:
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству.

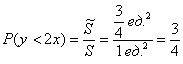
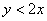
Ответ:

…я так и знал, что вы соскучились по неравенствам =) А они бывают не только линейными:

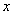
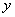
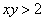
Загадываются два числа и в промежутке от 0 до 5. Какова вероятность, что ?

Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата

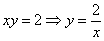
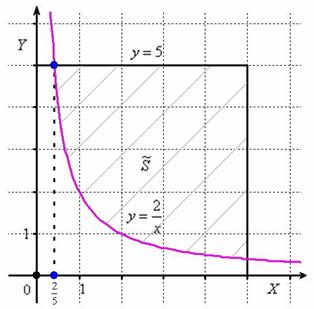
Изобразим ветвь гиперболы , которая делит квадрат на две части:

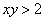
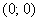
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять , и подставим её координаты в наше неравенство:

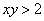
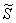
Получено неверное неравенство, а значит, условию соответствует «верхний кусок», площадь которого вычислим с помощью определённого интеграла.

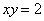
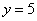
Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы и прямой ):

На отрезке прямая расположена не ниже гиперболы ,
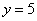
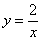
по соответствующей формуле:

По геометрическому определению:
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.

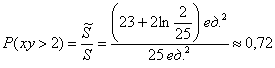
Ответ:

Аналогичный пример для самостоятельного решения:

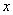
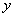
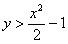
Загадываются два числа и в промежутке от 0 до 10. Какова вероятность, что ?

Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален. Моя версия решения совсем близко.

В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним демонстрационный пример с отрезком 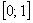, на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.

Надеюсь, ваше настроение значительно улучшилось и теперь вы обязательно справитесь со всеми учебными и внеучебными трудностями. …Не улучшилось?! Дополнительные задачи по теме можно найти в архиве готовых решений по сборнику Чудесенко =) =)

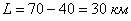
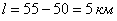
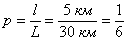
Задача 2: Решение: используем геометрическое определение вероятности. Общему числу исходов соответствует участок длиной , благоприятствующему количеству исходов – участок длиной . Таким образом:
– вероятность того, что обрыв провода произошёл между 50-м и 55-м километрами линии.
Ответ:

Задача 4: Решение: общему количеству исходов соответствует площадь круга:

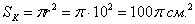
Площадь прямоугольного треугольника равна полупроизведению его катетов: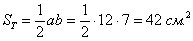

По условию поставленная в круг точка не должна попасть в треугольник, поэтому благоприятствующее число исходов выражается разностью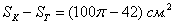
По геометрическому определению:
– вероятность того, что поставленная в круг точка не попадёт в треугольник.
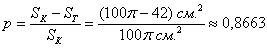
Ответ:

Задача 6: Решение: Оля и Коля могут встретиться в течение 60 минут. Выполним чертёж: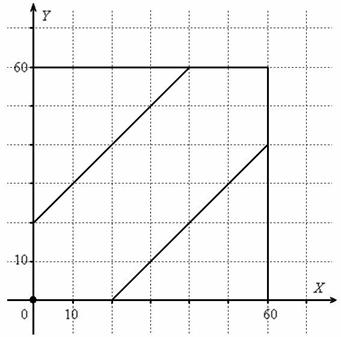

Площадь квадрата 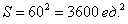соответствует общему числу исходов.
Рассмотрим противоположные события:
– Оля и Коля встретятся во время обеда;
– данной встречи не состоится.
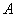
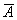
Вычислим суммарную площадь двух треугольников:
– данное значение благоприятствует событию .
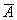
По геометрическому определению вероятности: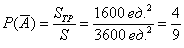

Противоположные события образуют полную группу, поэтому: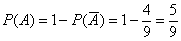

Ответ:

Задача 9: Решение: выполним чертёж: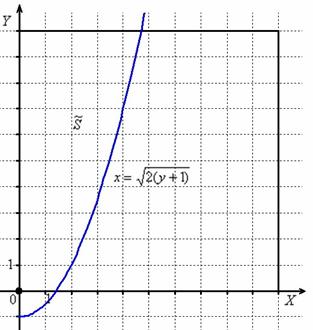

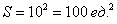
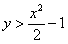
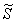
Общее число исходов выражается площадью квадрата . Неравенству соответствует площадь , которую вычислим с помощью определённого интеграла, интегрируя по «игрек» (данный метод рассмотрен в статье Объем тела вращения).
Выразим обратную функцию: .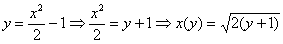
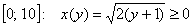
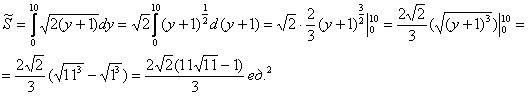
На отрезке , поэтому:

По геометрическому определению:
– вероятность того, что два загаданных от нуля до 10 числа будут удовлетворять неравенству
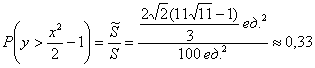
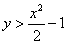
Ответ: