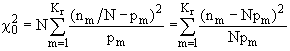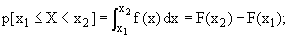Критерий значимости означает что
Статистические гипотезы, критерии значимости, критерии согласия



Статистическая гипотеза есть некоторое предположение относительно свойств генеральной совокупности, из которой извлекается выборка. Критерий статистической гипотезы—это правило, позволяющее принять или отвергнуть данную гипотезу на основании выборки. При построении такого правила используются определенные функций результатов наблюдений g(х1,х2. хN), называемые статистиками для проверки гипотез. Все возможные значения подобных статистик делятся на две части: область принятия гипотезы и критическую область. Проверка гипотезы сводится к выяснению того, попадает или нет конкретное значение статистики, вычисленное по выборке, в критическую область: если нет—гипотеза принимается, как не противоречащая результатам наблюдения, если да—гипотеза отвергается. При этом всегда возможно совершить ошибку; различные типы возможных ошибок указаны в табл. 2.2.
| Гипотеза | Объективно верна | Объективно неверна |
| Принимается | Правильное решение | Ошибка II рода |
| Отвергается | Ошибка I рода | Правильное решение |
Вероятность совершить ошибку I рода называется уровнем значимости критерия и обозначается q. Обычно уровень значимости выбирают равным 0,01; 0,1; 0,05 (последнее значение— наиболее часто).
Критерии значимости — это критерии, с помощью которых проверяют гипотезы об абсолютных значениях параметров или о соотношениях между ними для генеральных совокупностей с известной (с точностью до параметров) функцией распределения вероятностей.
Для пояснения идеи построения критериев значимости предположим, что некоторая оценка 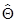
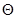
Даже если нулевая гипотеза справедлива, то выборочное значение 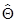
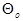
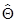
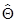
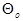
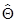
Вид критической области полностью определяется характером альтернативной гипотезы h1, т. е. гипотезы, противопоставляемой нулевой, той гипотезы, в пользу которой склоняется исследователь, отвергая проверяемую нулевую гипотезу.
Если нулевой гипотезе Но: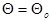
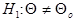
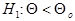
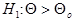
В табл. 2.3 приведены некоторые стандартные критерии, позволяющие проверять гипотезы о значениях математических ожиданий и дисперсий нормальных генеральных совокупностей при независимых наблюдениях в выборке.
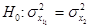
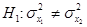
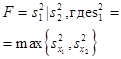
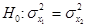
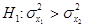
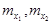 неизвестны
неизвестны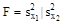
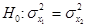
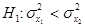
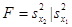
Критерием согласия называется критерий гипотезы о том, что генеральная совокупность имеет распределение предполагаемого типа (например, нормальное распределение). Существуют несколько критериев согласия: критерий согласия Пирсона, Колмогорова, и др. Процедура проверки согласия опытного и теоретического распределения случайной величины состоит в построении эмпирического распределения, полученного по независимым измерениям, случайной величины X, определении некоторой функции накопленных частот и сравнении ее с теоретической при заданном уровне значимости. Среди различных критериев согласия наиболее употребителен универсальный критерий согласия c 2 (Пирсона).
где F(x)— функция распределения вероятностей или интегральная функция распределения.
Закон распределения 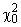
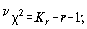
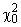
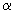
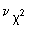
Если 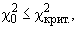
КРИТЕРИЙ ЗНАЧИМОСТИ
Полезное
Смотреть что такое «КРИТЕРИЙ ЗНАЧИМОСТИ» в других словарях:
критерий значимости — проверка по критерию значимости — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы проверка по критерию значимости EN significance test … Справочник технического переводчика
КРИТЕРИЙ ЗНАЧИМОСТИ — (test of significance) Статистический критерий, базирующийся на расчете вероятности того, что данный результат может быть получен в результате ошибки выборочного обследования. Например, оценка статистически значимо отличается от нуля при 5… … Экономический словарь
КРИТЕРИЙ — F критерий значимости для проверки гипотезы равенства стандартных отклонений σ1 = σ2 двух независимых выборок из нормальной совокупности соответственно объема n1 и n2. Если s21 и s22 выборочные оценки соответственно σ21, σ22,… … Геологическая энциклопедия
КРИТЕРИЙ СОГЛАСИЯ — см. Критерий значимости. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
КРИТЕРИЙ t, t-СТАТИСТИКА — (t test) Широко используемый критерий значимости (significance) статистических оценок. t статистика – это отношение стандартной ошибки оценки коэффициента к его абсолютной величине. Его конкретное значение можно сравнить с таблицами t статистик,… … Экономический словарь
Значимости уровень — статистического критерия, вероятность ошибочно отвергнуть основную проверяемую гипотезу, когда она верна. В теории статистической проверки гипотез З. у. называется вероятностью ошибки первого рода. Понятие «З. у.» возникло в связи с… … Большая советская энциклопедия
ЗНАЧИМОСТИ УРОВЕНЬ — статистического критерия вероятность ошибочно отвергнуть основную проверяемую гипотезу, когда она верна. В теории статистич. проверки гипотез 3. у. наз. вероятностью ошибки первого рода. Понятие 3. у. возникло в связи с задачей проверки… … Математическая энциклопедия
Критерий Фишера — (F критерий, φ* критерий, критерий наименьшей значимой разности) апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в… … Википедия
Критерий Лиллиефорса — статистический критерий, названный по имени Хьюберта Лиллиефорса, профессора статистики Университета Джорджа Вашингтона, являющийся модификацией критерия Колмогорова–Смирнова. Используется для проверки нулевой гипотезы о том, что выборка… … Википедия
ЗНАЧИМОСТИ КРИТЕРИЙ
Далее, по наблюденным значениям Х 1=150 и Х 2=117 вычисляют значение X 2 статистики критерия:
Поскольку 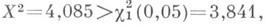
Лит.:[1] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [2] Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964; [3] Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; [4] Девятов Б. И., «Теория вероятн. и ее примен.», 1969, т. 14, № 1, с. 175-78.
Полезное
Смотреть что такое «ЗНАЧИМОСТИ КРИТЕРИЙ» в других словарях:
Критерий Фишера — (F критерий, φ* критерий, критерий наименьшей значимой разности) апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в… … Википедия
Критерий Лиллиефорса — статистический критерий, названный по имени Хьюберта Лиллиефорса, профессора статистики Университета Джорджа Вашингтона, являющийся модификацией критерия Колмогорова–Смирнова. Используется для проверки нулевой гипотезы о том, что выборка… … Википедия
Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия
КРИТЕРИЙ ЗНАЧИМОСТИ — правило проверки статистических гипотез, основанное на свойствах распределения меры отклонения эмпирической функции распределения выборки при одной гипотезе от эмпирической функции распределения при др. гипотезе. Эта мера определяется разл.… … Геологическая энциклопедия
Критерий согласия Пирсона — Критерий Пирсона, или критерий χ² (Хи квадрат) наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая… … Википедия
Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Данный критерий является многомерным обобщением критерия Уилкоксона Манна Уитни. Критерий Краскела Уоллиса является ранговым, поэтому он инвариантен по отношению к любому… … Википедия
Критерий Дарбина — Критерий Дарбина Уотсона (или DW критерий) статистический критерий, используемый для тестирования автокорреляции первого порядка элементов исследуемой последовательности. Наиболее часто применяется при анализе временных рядов и… … Википедия
Критерий Дарбина-Уотсона — (или DW критерий) статистический критерий, используемый для нахождения автокорреляции остатков первого порядка регрессионной модели. Критерий назван в честь Джеймса Дарбина и Джеффри Уотсона. Критерий Дарбина Уотсона рассчитывется по следующей… … Википедия
Критерий Пирсона — Критерий Пирсона, или критерий χ2 наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической … Википедия
критерий значимости — проверка по критерию значимости — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы проверка по критерию значимости EN significance test … Справочник технического переводчика
Проверка статистических гипотез
п.1. Понятие о статистической гипотезе
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| \(H_0\) | \(H_1\) | ||
| Принятая гипотеза | \(H_0\) | True Negative \(H_0\) принята верно | False Negative \(H_0\) принята неверно Ошибка 2-го рода |
| \(H_1\) | False Positive \(H_0\) отвергнута неверно \(H_1\) принята неверно Ошибка 1-го рода | True Positive \(H_0\) отвергнута верно \(H_1\) принята верно | |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Уровень значимости при проверке гипотезы
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости \(p\) | Решение о гипотезе \(H_0\) | Вывод для гипотезы \(H_1\) |
| \(p\gt 0,1\) | \(H_0\) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| \(0,5\lt p\leq 0,1\) | Истинность \(H_0\) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| \(0,01\lt p\leq 0,05\) | Отклонение \(H_0\), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| \(p\leq 0,01\) | Отклонение \(H_0\), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы \(H_1\).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с \(n\geq 100\) критический уровень снижают до α=0,01.
п.3. Критическая область
Различают 3 вида критических областей
п.4. Простая гипотеза и критерии согласия
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
\(H_0\): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
п.5. Критерий согласия \(X^2\) Пирсона
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| \(m_i\) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| \(f_i-m_i\) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| \(\frac<(f_i-m_i)^2> | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| \(m_i\) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| \(f_i-m_i\) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| \(\frac<(f_i-m_i)^2> | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(p_i\) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: \(X_e^2=36,84\)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для \(X_<кр>^2=X^2(\alpha,k-2)\).
Для уровня значимости α=0,05 и k=8, r=1 находим:
\(X_<кр>^2\approx 12,59\)
Получается, что: \(X_e^2\gt X_<кр>^2\)
Гипотеза \(H_0\) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x= <4;5;6;7>с редким числом попаданий:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 8 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 35 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(p_i\) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: \(X_e^2=1,12\)
Критическое значение статистики ищем в виде \(X_<кр>^2=X^2(\alpha,k-2)\), где α=0,05 и k=5, r=1
\(X_<кр>^2\approx 7,81\)
Получается, что: \(X_e^2\lt X_<кр>^2\)
Гипотеза \(H_0\) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики \(X_e^2\) в Примере 2, основной вклад внесло слагаемое для \(x_i=7\). Оно равно 34,34 и поэтому сумма \(X_e^2=36,84\) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты \(x_i=4,375\) слагаемое статистики равно 0,16 и сумма \(X_e^2=1,12\) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.