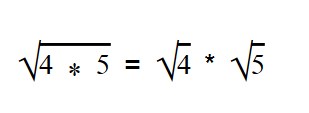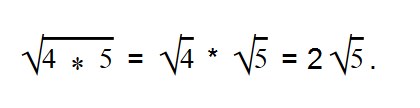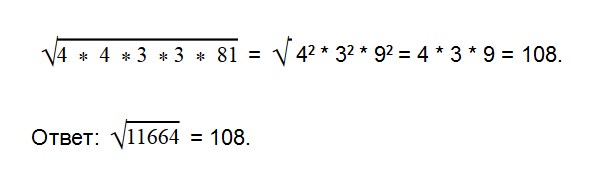Корень поделить на корень что будет

Действия с корнями.

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Деление корней с одинаковыми и разными показателями

Чтобы разделить корни с одинаковыми показателями, нужно разделить подкоренные выражения, а показатель корня оставить прежний.

Если показатели корней разные, то сначала нужно привести корни к общему показателю, а потом — поделить получившиеся корни с одинаковыми показателями.Можно делить (число на корень или корень на число) — для этого нужно занести под знак корня (в числитель или в знаменатель) это число, возведённое в степень с показателем, как у корня.

Возведение корней в степень

Чтобы возвести корень в степень, нужно возвести в эту степень подкоренное выражение, а показатель корня оставить тем же.
(∛‎(125)) 2 = (∛‎(125 2 ))

Извлечение корня из корня

Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить прежним.

Уничтожение иррациональности в знаменателе

Чтобы избавиться от иррациональности в знаменателе, нужно домножить на одно и то же выражение числитель и знаменатель дроби, пользуясь по мере надобности формулами сокращённого умножения. Если в знаменатетеле дроби корень числа — домножаем на такой же корень, и в знаменателе оказывается само число.

Если в знаменателе дроби сумма/разность корней двух чисел — домножаем на разность/сумму этих корней, и в знаменателе оказывается разность самих чисел.

Если в знаменателе сумма/разность кубических корней двух чисел — домножаем на неполный квадрат разности/суммы этих кубических корней. В знаменателе получается сумма/разность самих чисел.Если в знаменателе неполный квадрат суммы/разности кубических корней двух чисел — домножаем на разность/сумму этих кубических корней. В знаменателе получается разность/сумма самих чисел.

Источник

Корень и его свойства

Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.

Определение «Корень»

Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).

Формула: √ a 2 = a

Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.

Извлечение корней: примеры

Найти корень из числа можно одним из следующих способов:

Приведение корней с разными показателями

Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.

Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.

Корень: сложение и вычитание корней

Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.

Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.

Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Корень: умножение

Умножение корней без множителей

Произведение корней из чисел равно корню из произведения этих чисел.
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2

Умножение корней с множителями

При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6

Корень: деление

Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.

Деление корней без множителей

Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7

Деление квадратных корней с множителями

Примеры для практики

Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«

Источник

Корень поделить на корень что будет

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Продолжаем развлечение? В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам. Очень уж она полезная в решении примеров! Осталось ещё две. Переходим к следующей формуле. Это будет деление корней.

Формула столь же проста, как и умножение. Вот она:

У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.

Как делить корни?

Элементарно. Вот вам примерчик:

В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования. Например:

Здесь мы превратили двойку в корень квадратный из четырёх. Исключительно для того, чтобы формулу деления корней в дело употребить. Как видите, ничего здесь сложного нет.

Рассмотрим формулу деления корней в обратном направлении. Справа налево. Вот так:

Какие возможности раскрывает нам такая запись? Ничего нового, думаете? Ошибаетесь! Забавно, но простая запись формулы в другом направлении частенько высвечивает дополнительные возможности!

В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Например, пусть нам надо извлечь квадратный корень из дроби 25/144. Спокойно пишем себе:

Что, забыли, как переводить дроби? Срочно двигайте в тему «Дроби» и вспоминайте. А то ни дробь преобразовать, ни сократить её. И зачем вам тогда квадратные корни?

Надеюсь, что деление корней проблем не составляет. Простая и безобидная формула, простое употребление. Теперь в нашем арсенале уже две формулы. Умножение и деление корней. Табурет на двух ножках. Сидеть можно, но. некомфортно.)

Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.

Но именно эти действия вызывают массу проблем. С этим надо разобраться основательно. Что мы сейчас и сделаем. Начнём с безобидного действия. С корня в квадрате.

Как возвести корень в квадрат?

Так как посчитать корень в квадрате? Очень просто. Прямо по смыслу корня. Что такое корень квадратный из двух, например? Это число, которое при возведении в квадрат должно дать двойку. Так вот, если мы число, которое при возведении в квадрат должно дать двойку, возведём-таки в этот самый квадрат? Что получим? Двойку, конечно! Т.е. подкоренное выражение. Или, в общем виде:

А если корень не в квадрате, а в другой степени? Не вопрос! Если, конечно, знаете действия со степенями. По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Например, вот так (расписываю подробно):

Как видим, корень исчезает, Степень результата в два раза меньше исходной степени.

Как извлечь корень из квадрата?

Пусть у нас есть хорошее число 2. Возведём его в квадрат.

Кто бы спорил? А теперь давайте обратно, извлечём из результата квадратный корень:

Опять всё чудесно, правда? С чего начали, к тому и вернулись! Стало быть, можно записать:

Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:

Для таких преобразований надо опять-таки знать действия со степенями, но тут уж ничего не поделаешь.

Теперь по формуле корня из квадрата:

Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Как только в игру вступают отрицательные величины, простота куда-то пропадает начисто. Вернём эту простоту и ясное понимание.

Вот тут и будет мрачный заяц. Для лучшего запоминания.) Концентрируем внимание и собираем весь интеллект в кулак!)

Итак, откуда в корнях могут появиться отрицательные числа и выражения?

Пунктик первый. Отрицательные значения даны прямо в задании. Вспоминаем пример корня из квадрата двойки:

Здесь всё понятно и просто.

А теперь попробуем вычислить:

Берём, и просто считаем, безо всяких формул:

А если бы мы использовали формулу:

получили бы не два, а минус два! Что является ошибкой.

Не работает эта формула для отрицательных значений.

Для того, чтобы формула корня из квадрата работала для всех значений а, она записывается вот так:

Это и есть последнее, третье свойство корней. Корень из квадрата. Третья ножка для табурета.)

Здесь появляется страшный значок для старшеклассников. Модуль. Если вы пока не сильны в раскрытии модулей, не волнуйтесь. Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Формула стала полноценной. Модуль просто отсекает минусы:

Пунктик второй. Отрицательные значения спрятаны в буквах и дополнительных условиях. Например, требуется упростить выражение:

Не выходит? Смотрим ЗАКЛЮЧЕНИЕ урока.

Получилось? Неплохо. А как вам эти примерчики?

Не всё понятно? Не беда. Читаем дальше.

Не получаются даже простые примеры? Или не очень простые? Хотелось бы увидеть решение всех примеров с подробными и понятными объяснениями? Нет проблем! Идём в Особый раздел 555. Квадратные корни. Там даны все разъяснения. Которые, между прочим, годятся не только для решения этих примеров.

Это и будет последняя, четвёртая ножка для табурета.) Которая не даст свалиться и при серьёзных заданиях.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Деление корней: правила, методы, примеры

Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.

Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.

Метод 1. Деление подкоренных выражений

Записать дробь

Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.

Использовать один знак корня

В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.

Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.

Разделить подкоренные выражения

Просто разделите одно выражение на другое, а результат запишите под знаком корня.

Упростить подкоренное выражение (если необходимо)

Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.

Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.

Метод 2. Разложение подкоренного выражения на множители

Записать дробь

Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.

Разложить на множители каждое из подкоренных выражений

Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.

8 36 = 2 × 2 × 2 6 × 6

Упростить числитель и знаменатель дроби

Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.

Рационализировать знаменатель (избавиться от корня)

В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него.

Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.

6 2 3 × 3 3 = 6 2 × 3 3 × 3 = 6 6 9 = 6 6 3

Упростить полученное выражение (если необходимо)

Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.

2 6 упрощается до 1 3 ; таким образом 2 2 6 упрощается до 1 2 3 = 2 3

Метод 3. Деление квадратных корней с множителями

Упростить множители

Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!

Упростить квадратные корни

Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.

Умножить упрощенные множители на упрощенные корни

Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.

Рационализировать знаменатель (избавиться от корня в знаменателе)

4 3 7 × 7 7 = 4 3 × 7 7 × 7 = 4 21 49 = 4 21 7

Метод 4. Деление на двучлен с квадратным корнем

Определить, находится ли двучлен (бином) в знаменателе

Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.

1 5 + 2 — в знаменателе присутствует бином, поскольку есть два одночлена.

Найти выражение, сопряженное биному

Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.

Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе

Советы:

Источник

Что такое квадратный корень

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

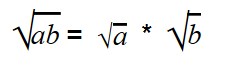Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

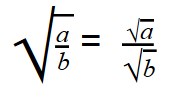Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

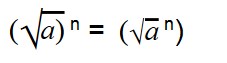Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10

Источник