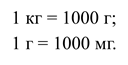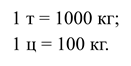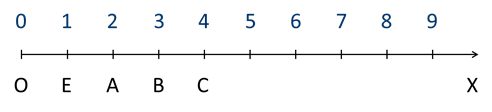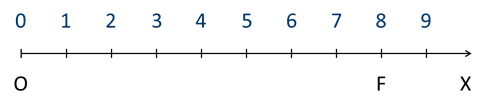Координаты что это в математике 5 класс
Шкалы и координаты
Урок 5. Математика 5 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Шкалы и координаты»
На этом уроке мы поговорим о величинах. Посмотрим, как измеряются различные величины и для чего они используются. Разберёмся в понятиях «шкала», «координатный луч» и «координата».
К уроку вы должны были подготовиться и принести линейки. Положите, пожалуйста, линейку перед собой.
Обратите внимание на то, что у всех они разные: разного цвета, разного материала и разной длины. Но все линейки имеют общие черты – на них нанесены штрихи.
Все штрихи находятся на одинаковом расстоянии друг от друга. Около некоторых штрихов написаны числа. Все штрихи на линейке разбивают её на равные части. Эти части называют делениями. Длину деления называют ценой. Цена деления на вашей линейке равна 1 мм. Все деления линейки вместе с написанными числами образуют шкалу. Линейки используют для измерения длины.
Давайте измерим длину отрезка АВ.
Приложим к нему линейку.
Видим, что длина отрезка АВ равна 6 см.
Шкалы имеют и другие измерительные приборы, например комнатный термометр.
Используют его для измерения температуры. Его шкала состоит из 55 делений. Каждое деление соответствует одному градусу Цельсия. Посмотрите: какую температуру показывает термометр на рисунке? Правильно! 15 °С.
Шкалы могут иметь различные формы. Например, спидометр:
На его шкале на промежутке от 0 км/ч до 20 км/ч содержится 4 деления. Поэтому одному делению шкалы соответствует 20 км/ч : 4 = 5 км/ч. Значит, каждое деление спидометра соответствует 5 км/ч. С помощью спидометра контролируют скорость автомобиля.
На весах тоже бывают шкалы:
На рисунке видно, что масса яблок равна 2 кг. При взвешивании меньших предметов применяют единицы массы: грамм (г) и миллиграмм (мл).
При взвешивании больших предметов применяют единицы массы: тонну (т) и центнер (ц).
А вспомним механические часы или часы с циферблатом:
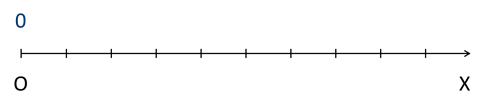
Со шкалами мы разобрались, а теперь давайте перейдём к чертежам. Начертим луч ОХ, так чтобы он шёл слева направо. Его начало, точку О, пометим числом 0.
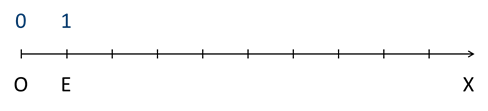
Отметим на луче ОХ некоторую точку Е и пометим её числом 1. Получили отрезок ОЕ, его длину примем равной единице.
Такой отрезок называют единичным отрезком.
Отложим на луче ОХ вправо от точки Е такой же единичный отрезок. Получим новую точку, обозначим её А, а над ней запишем число 2. Повторим это ещё раз, получим точку В, которую пометим числом 3. Этот процесс можно повторить бесконечное количество раз. В результате получится бесконечная шкала.
Её называют координатным лучом, а точку О – началом отсчёта.
И так как конца у координатного луча нет, то завершим его стрелочкой, которая нам будет показывать, что числа продолжаются и дальше.
Натуральное число изображается определённой точкой координатного луча. Например, число 3 изображается точкой В. Говорят, что число 3 является координатой точки В или точка В имеет координату 3.
Это записывают так: В (3).
Координата точки показывает расстояние от этой точки до начала координат, измеренное единичным отрезком.
На рисунке точка F имеет координату 8. Это говорит о том, что расстояние от точки F до точки О равно 8, или отрезок ОF имеет длину 8 (ОF = 8).
Итак, сегодня на уроке мы рассмотрели различные величины и их единицы измерения. Узнали такое понятие, как шкала. Научились строить координатный луч и находить точки по их координатам.
Шкалы, координаты
Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.
Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.
Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).
Рисунок 1. Измерительная линейка.
Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.
Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).
Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.
Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.
Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.
Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.
Рисунок 2 Цена деления шкалы
Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?
Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:
Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.
Координатный луч, единичный отрезок, координаты точки
Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.
Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.
Рис. 3. Луч с началом в точке O
Рис. 4. Луч с равными отрезками
Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).
Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.
Рис. 5. Луч с отрезками и цифрами
Покажу еще раз на примере точки S :
так как RS=OP (по условиям построения данных отрезков),
подставив известные нам значения длины отрезков OR и OP, получим:
Значит, точке S на нашем лучу соответствует число 3.
Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.
Рис. 6. Координатный луч
Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.
Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.
Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.
Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.
Координатный луч — это не что иное, как бесконечная шкала.
Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.
Рис. 7. Разные варианты единичного отрезка
Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).
Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.
Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.
Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.
Рис. 8. Координаты точек
Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).
В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.
Рис. 9. Большие числа на координатном луче.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.1 / 5. Количество оценок: 8
Шкалы и координаты
Шкалы
Вот неполный перечень предметов, которые дают нам представление о шкале (деления на весах, на спидометре, на часах, на линейке, на градуснике).
Рассмотрим внимательно такую знакомую ученическую линейку:
На линейке нанесены штрихи, которые разбивают ее на равные части – деления.
Длина одного деления составляет 1 мм. Вместе эти деления образуют шкалу.
С помощью линейки можно измерить длину отрезка:
На рисунке отрезок АВ имеет длину 12 см (АВ = 12 см).
С помощью шкалы комнатного термометра измеряют температуру воздуха в помещении.
Одно деление равно 1°С (один градус Цельсия).
На рисунке термометр показывает температуру 24ºС.
Единицы массы
С помощью шкалы кухонных весов измеряют массу каких – либо продуктов.
На рисунке масса лука равна 800 г. (Вспомните, что 1 000 г = 1 кг).
При взвешивании предметов большой массы, применяют единицы массы: тонна (т), центнер (ц).
Одна тонна равна 1 000 кг.
Один центнер равен 100 кг.
Пишут: 1 т = 1 000 кг, 1 ц = 100 кг.
Единичный отрезок
Построим луч MN (слева направо, M – начало луча).
Отложим от начала луча вправо несколько одинаковых отрезков и выполним следующие действия: внизу под лучом каждое деление отметим буквой (выбираем произвольно), а сверху луча над делениями запишем цифры по порядку, начиная с начала луча – точки M (это будет цифра 0).
Отрезок MA называется единичным отрезком.
Координаты
Откладывая дальше единичные отрезки, получим бесконечную шкалу.
Ее называют координатным лучом. Для удобства, вместо точек ставят штрихи (короткие вертикальные черточки).
Записывают: M(0), A(1), B(2), C(3), D(4), E(5), F(6), K(7) и т.д.
Поделись с друзьями в социальных сетях:
Математика. 5 класс
Конспект урока
Представление натуральных чисел на координатном луче
Перечень рассматриваемых вопросов:
— изображение чисел точками на координатной прямой;
— нахождение координат отмеченной точки;
— сравнение натуральных чисел по их расположению на координатном луче.
Луч – прямая линия, которая имеет начало, но не имеет конца.
Координатный луч – это луч, на котором задано направление, а также отмечены начало отсчёта и единичный отрезок.
Начало отсчёта – особая точка, обычно обозначаемая буквой О, которая используется как точка отсчёта для всех остальных точек.
Единичный отрезок – величина, принимаемая за единицу при геометрических построениях.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Как вы уже знаете, для пересчёта предметов используют натуральные числа. Сегодня мы будем представлять их на координатном луче.
Для начала рассмотрим, чем отличается координатный луч от луча.
Вспомним, что такое луч. Луч – это прямая линия, которая имеет начало, но не имеет конца. А теперь рассмотрим координатный луч. Для этого зададим луч. Начало луча обозначим точкой О сверху, а снизу под началом луча подпишем число 0. Точку О примем за начало отсчёта. Говорят, что точка О имеет координату 0 и пишут О(0). Далее на луче, начиная с точки О, отложим выбранный единичный отрезок ОА, под точкой А запишем число 1. Говорят, что точка А имеет координату 1. Отложим единичный отрезок от точки А вправо несколько раз и запишем, соответственно, числа 2, 3, 4 и так далее, обозначив эти точки буквами В, С, D и так далее. Говорят, что точка В имеет координату 2, С – координату 3…
Координатный луч мы будем чертить слева направо, выходящим из точки О в направлении, отмеченном стрелкой. Отмерим на координатном луче единичный отрезок, длину которого будем принимать за единицу при определении координат.
А теперь свяжем натуральные числа и координатный луч.
Известно, что ряд натуральных чисел начинается с единицы. За каждым натуральным числом в ряду следует ещё одно натуральное число, большее предшествующего на единицу. Такая же структура и у координатного луча. Поэтому числа удобно представлять в виде точек на координатном луче.
Обратите внимание, что координатный луч напоминает линейку, на которой отмечены числа 0, 1, 2, 3 и так далее – с той лишь разницей, что любая линейка ограничена (конечна), а координатный луч неограничен (бесконечен).
А теперь зададимся вопросом, как изобразить точку D с координатой 45?
Ответ прост: изменим масштаб координатного луча, например, так, чтобы один единичный отрезок соответствовал 10. Тогда точка D будет серединой отрезка с концами в точках с координатами 40 и 50.
Заметим, что если на координатном луче точка M лежит правее точки N, то она будет соответствовать большему числу. Так натуральные числа можно сравнивать при помощи координатного луча.
А теперь отметим точку Р, которая будет правее точки М. Следовательно, точка Р будет больше точек М и N.
Таким образом, мы получим иллюстрацию одного очень интересного свойства: если первое число меньше второго, а второе меньше третьего, то первое меньше третьего. Это свойство транзитивности натуральных чисел.
Итак, сегодня мы познакомились с понятием координатный луч и научились изображать числа точками на координатном луче.
Изображение точек на координатной прямой.
Начертим координатный луч, исходя из условия задания: точки О, С, А имеют следующие координаты: О(0), С(2) и А(5), отрезок СА = 6 см.
Решение: по условию задачи начертим координатный луч. Отметим на нём точку О(0) (с координатой). Далее следует задать единичный отрезок. Определим его следующим образом: от точки С до точки А умещается три единичных отрезка – это можно определить по координатам точек С и А.
5 – 2 = 3 (единичных отрезка)
Теперь найдём длину одного единичного отрезка. Для этого длину отрезка АС поделим на три единичных отрезка, входящих в отрезок АС.
6 см : 3 единичных отрезка = 2 см в единичном отрезке.
Назовём единичный отрезок ОМ = 2 см, следовательно, координаты точки – М(1).
Теперь изобразим полученный луч.
№ 1. Выберите правильный ответ. Какая из точек – С(78), D(45), М (15), Р(24) – расположена правее других?
При выполнении данного задания нужно использовать правило сравнения чисел с помощью координатного луча. Чем большему числу соответствует координата точки, тем правее она будет расположена на координатном луче.
Правильный ответ: точка С.
№ 2. Напишите координаты точек D, Е, Т и К, отмеченных на координатном луче.
Каждая точка имеет координату, соответствующую натуральному числу, который отсчитывается от 0 по единичным отрезкам.
Таким образом, правильными ответами будут: Е(2); D(4); Т(10); К(12).
Конспект урока по математике в 5 классе на тему «Шкалы и координаты»
Конспект урока по математике в 5 классе
Тип урока: урок получения новых знаний
Шкалы и координаты
Образовательная: пр одолжить работу по формированию вычислительных навыков.
Воспитательная: воспитывать аккуратность при работе на доске и в тетрадях, рационально распределять отведенное время.
Развивающая: развивать познавательный интерес учащихся, умение обрабатывать информацию.
Планируемые результаты: изучить шкалы, координаты точек, а также уметь находить по шкале определенную величину и определять координату точки на координатном луче.
Познавательные УУД: логические – анализ объектов с целью выделения признаков.
Коммуникативные УУД: планирование учебного сотрудничества с учителем и одноклассниками.
Регулятивные УУД: целеполагание.
Личностные УУД: самоопределение.
фронтальная, индивидуальная, групповая.
Долгожданный дан звонок –
Тут затеи и задачи,
Игры, шутки, все для вас!
Пожелаем всем удачи –
За работу, в добрый час!
2. Самостоятельная работа
Проверочный тест (приложение 1).
Выполняют самостоятельную работу
3. Определение темы урока
— Как называется инструмент, при помощи которого измеряют длину отрезка?
— Рассмотрите линейку. Деления, которые вы на ней видите, образуют шкалу.
— Вспомните и назовите приборы и инструменты, на которых есть шкалы.
Сегодня на уроке мы будем изучать шкалы и координаты.
— Какое слово вам непонятно?
— Понять значения новых слов нам поможет учебник.
Термометр, транспортир, весы, спидометр и др.
4. Работа по учебнику
1. С. 21—22 (работа по статье учебника).
— Прочитайте статью учебника и приготовьтесь отвечать на вопросы.
— Какие понятия связаны с координатным лучом?
— Расскажите, как построить координатный луч.
2. На доске начерчен координатный луч с отмеченными на нем точками А, В, С, D, М, К.
— Покажите начало координатного луча.
— Покажите единичный отрезок.
— Запишите координаты точек D, М, К.
4. С. 23, № 109 (работа в паре).
5. С. 23, № 110 (письменно).
— Сколько делений между числами 10 и 30?
— Чему равно одно деление?
— Запишите координаты точек.
5. Работа над задачей
— Сколько машин перевозило зерно?
— По сколько зерна перевозила первая машина за один рейс?
— Что сказано про вторую машину?
— Что известно про третью?
(В ходе анализа данных составляется таблица с кратким условием.)
— Что необходимо знать, чтобы выяснить, сколько зерна перевезла каждая машина?
— Можем ли найти грузоподъемность второй машины?
— Как узнать грузоподъемность второй машины?
— Можем ли узнать, сколько зерна перевезли три машины за один рейс?
— Сколько таких поездок было?
— Составьте план решения задачи.
(Полезно рассмотреть и второй способ решения.)
— Подумайте, как бы вы решали эту задачу, если бы машины сделали разное количество рейсов.
— Решите другим способом.
— Какое решение вам понравилось больше? Почему?
1) 3 + 1 = 4 (т) — грузоподъемность второй машины.
2) 4 : 2 = 2 (т) — грузоподъемность третьей машины.
3) 3 + 4 + 2 = 9 (т) — перевозят три машины за один рейс.
4) 9 ∙ 3 = 27 (т) — перевезут три машины за три рейса.
1) 3 ∙ 3 = 9 (т) — перевезла первая машина.
2) 3 + 1 = 4 (т) — грузоподъемность второй машины.
3) 4 ∙ 3 = 12 (т) — перевезла вторая машина.
4) 4 : 2 = 2 (т) — грузоподъемность третьей машины.
5) 2 ∙ 3 = 6 (т) — перевезла третья машина.
6) 9 + 12 + 6 = 27 (т) — перевезли всего зерна.
6. Повторение изученного материала. Комбинаторная задача
— Что вы можете о ней сказать?
— Сколько человек в команде?
— Рассмотрим вариант, когда вратарь не может быть капитаном команды.
— Сколько вариантов выбора капитана существует?
— Сколько существует вариантов выбора вратаря для выбранного капитана?
— Сколькими способами можно выбрать капитана и вратаря?
— Как вы думаете, изменится ли решение задачи, если вратарь может быть капитаном?
— Сколько способов выбора существует при этом условии?
7. Выполнение заданий
С. 26, № 136 (работа в паре с последующей проверкой).
8. Подведение итогов урока, рефлексия
— Объясните, что такое координатный луч.
— О чем нужно помнить при построении координатного луча?
— Устно закончите следующие предложения:
«На сегодняшнем уроке я понял, я узнал, я разобрался…»;
«Я похвалил бы себя…»;
«Особенно мне понравилось…»;
«После урока мне захотелось…»;
«Сегодня мне удалось…»;
9. Домашнее задание
С. 26, № 137, 138; с. 27, № 144 (а).
Приложение 1
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-083810
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Новые аккредитационные показатели для вузов вступят в силу с 1 марта
Время чтения: 1 минута
В школах Тюмени запустят раздельный сбор отходов
Время чтения: 1 минута
В России утверждены новые аккредитационные показатели для школ и колледжей
Время чтения: 2 минуты
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.