Контрольные суммы что это
Как узнать контрольную сумму файла в Windows
При скачивании ISO образов и архивов больших размеров всегда есть вероятность получить «битый» файл. Во времена Dial-UP такое было сплошь и рядом. И хотя сейчас такое случается намного реже, чтобы убедиться, что перед вами «оригинальный» файл придумали контрольные суммы, которые вычисляются на основе содержимого и позволяют заметить несоответствие даже одного байта.
То есть, если вы измените один байт в проверяемом файле, то и контрольная сумма такого файла так же изменится.
Для чего нужны контрольные суммы
У контрольных сумм две задачи:
Зная контрольную сумму оригинала, можно проверить является ли ваша копия подлинной.
Как вычислить контрольную сумму он-лайн
Контрольную сумму можно проверить он-лайн. Но я не буду рекомендовать этот способ, так как если размер вашего файла несколько ГигаБайт, то это займет много времени и всегда есть вероятность ошибки при передаче файла. Кроме того делиться своими файлами со сторонними сервисами не правильно.
Как узнать контрольную сумму файла в Windows
Разумнее вычислить контрольную сумму локально на своем компьютере. Это быстро и конфиденциально. В этой статье я опишу несколько способов получения контрольных сумм, как с помощью сторонних программ, так и непосредственно с помощью самой операционной системы Виндовс.
Файловый менеджер Total Commander
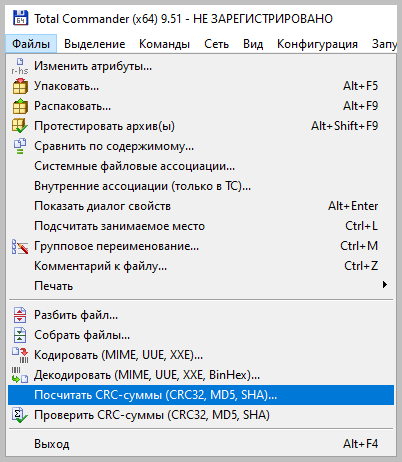
Total Commander — это популярный файловый менеджер, работающий на платформах Microsoft Windows и Android. В нем есть встроенная функция вычисления контрольных сумм.
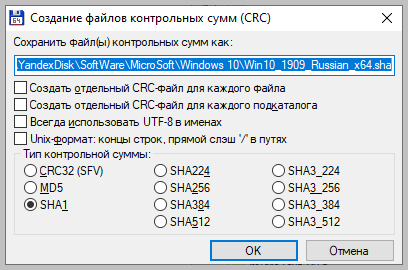
После чего вы можете выбрать один из алгоритмом вычисления контрольных сумм.
По-умолчанию Total Commander создает файл с именем проверяемого и с расширением по имени выбранного алгоритма расчета контрольной суммы.
Файловый архиватор 7-Zip
7-Zip — свободный, бесплатный файловый архиватор с высокой степенью сжатия данных. Он поддерживает несколько алгоритмов сжатия и множество форматов данных, включая собственный формат 7z c высокоэффективным алгоритмом сжатия LZMA.
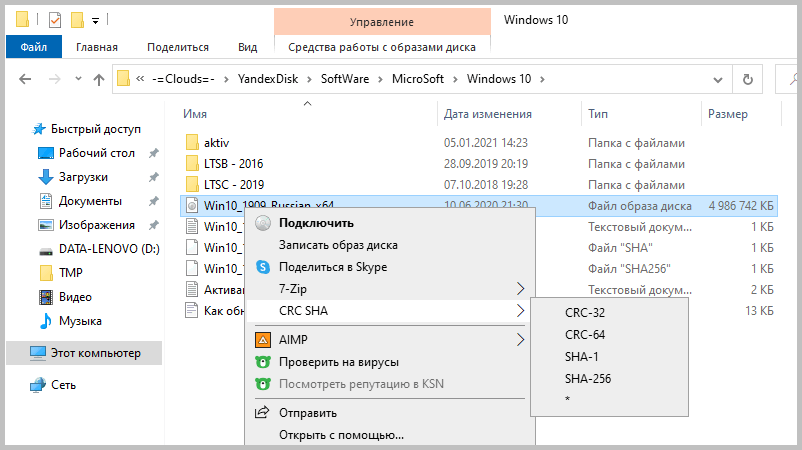
Этот архиватор имеет встроенную функцию вычисления контрольных сумм. Запустить ее можно прямо из контекстного меню Windows:
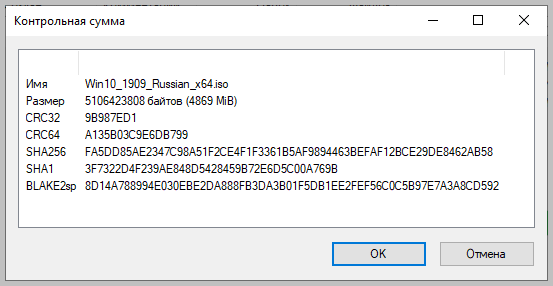
Если выбрать «звездочку», то программа подсчитает сразу несколько контрольных сумм:
Полученные данные можно выделить и скопировать в текстовый документ.
Как подсчитать контрольную сумму файла из консоли Windows
Чтобы посчитать контрольную сумму совсем не обязательно устанавливать специальные программы. И если вы не пользуетесь упомянутыми выше, то можете рассчитать контрольную сумму прямо из командной строки операционной системы.
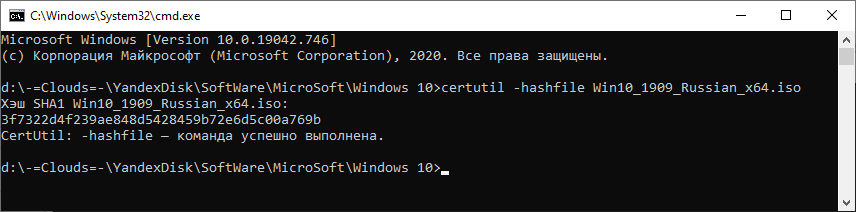
Например, чтобы посчитать контрольную сумму SHA1 с помощью утилиты CertUtil нужно запустить командную строку Windows 10, 8 или Windows 7 и ввести следующую команду:
Вот пример ее работы через несколько минут:
Считаем контрольную сумму в PowerShell
PowerShell — это средство автоматизации от Microsoft, с интерфейсом командной строки и языка сценариев, работает и включена в состав Windows 8 и новее.
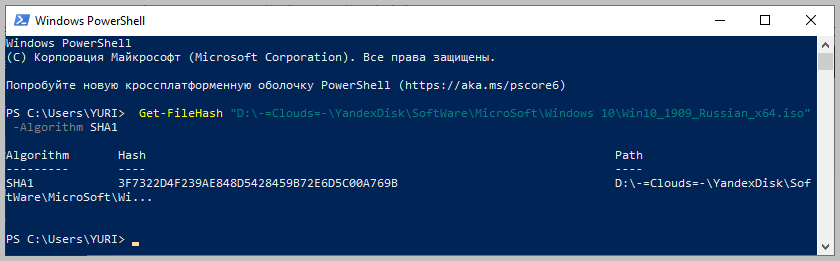
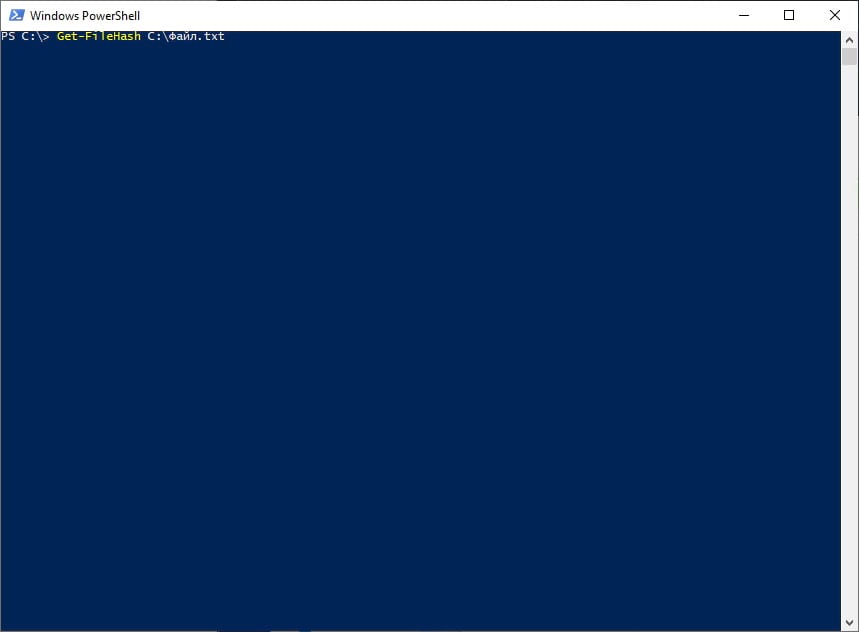
Чтобы вычислить контрольную сумму файла необходимо выполнить команду Get-FileHash указав через пробел имя файла и алгоритм вычисления контрольной суммы:
Обратите внимание, что полный путь и имя файла лучше заключить в двойные кавычки.
По-умолчанию, если не указать тип контрольной суммы, то будет посчитана SHA-256.
Для алгоритмов вычисления контрольной суммы в Windows PowerShell поддерживаются следующие значения:
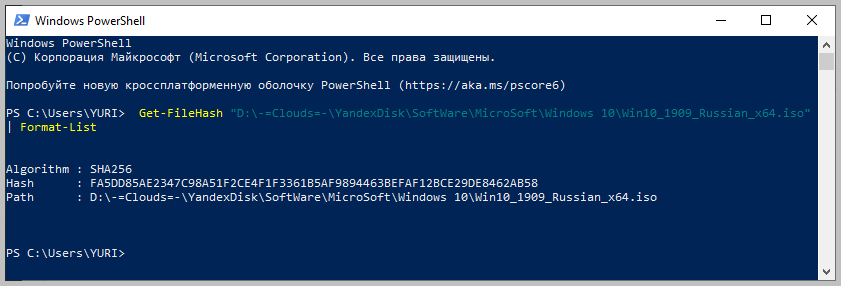
Для оформления вывода в виде списка можно использовать параметр | Format-List. Например:
Тогда результат работы будет выглядеть так:
Подробнее об использовании команды Get-FileHash можно прочитать на официальном сайте Microsoft — https://docs.microsoft.com/ru-ru/powershell/module/microsoft.powershell.utility/get-filehash
Какой алгоритм вычисления контрольных сумм самый правильный
MD5, SHA-1, SHA-256 и прочие – это разные алгоритмы хеш-функции. Хэши являются результатом работы криптографических алгоритмов, и представляют собой строку символов. Часто эти строки имеют фиксированную длину, независимо от размера входных данных.
MD5 самый быстрый, считается устаревшим, а SHA-256 имеет наименьшую вероятность коллизии, когда два разных файла имеют одинаковую контрольную сумму.
Для проверки целостности файла вам следует использовать тот, который предоставляет издатель. Если у вас на выбор есть несколько контрольных сумм, то лучше выбрать в следующей последовательности MD5, SHA-1, SHA-256, последний вариант является более предпочтительным.
Выводы
Если вы сомневаетесь в целостности скаченных файлов из интернета, особенно когда это касается оригинальных образов операционных систем, то проверьте их контрольную сумму. Сделать это можно как с помощью уже имеющихся у вас программ, так и воспользовавшись встроенными средствами операционной системы Windows.
Что такое контрольная сумма файла
К онтрольная сумма — это последовательность цифр и букв, используемая для проверки данных на наличие ошибок. Если Вам известна контрольная сумма исходного файла, Вы можете использовать специальную утилиту чтобы убедиться, что Ваша копия идентична.
Объяснение контрольных сумм
Чтобы получить контрольную сумму, Вы запускаете программу, которая обрабатывает этот файл алгоритмом. Типичные алгоритмы, используемые для этого, включают MD5, SHA-1, SHA-256 и SHA-512.
Алгоритм использует криптографическую хеш-функцию, которая принимает входные данные и создает строку (последовательность цифр и букв) фиксированной длины. Входным файлом может быть небольшой файл размером 1 МБ или большой файл размером 4 ГБ, но в любом случае Вы получите контрольную сумму такой же длины. Контрольные суммы также могут называться «хешами».
Небольшие изменения в файле приводят к иному виду контрольных сумм. Например, два разных текстовых файла, которые почти одинаковы, но у одного есть восклицательный знак, а у другого — точка будут иметь разные контрольные суммы. Разница в один символ в файле дает другую контрольную сумму.
Когда контрольные суммы полезны
Вы можете использовать контрольные суммы для проверки файлов и других данных на наличие ошибок, возникающих во время передачи или хранения. Например, файл мог быть неправильно загружен из-за проблем с сетью или проблемы с жестким диском могли вызвать повреждение файла на диске.
Если Вы знаете контрольную сумму исходного файла, Вы можете запустить для нее утилиту хеширования. Если полученная контрольная сумма совпадает, Вы знаете, что файл у Вас идентичен.
Компьютеры используют методы контрольной суммы для проверки данных на наличие проблем в фоновом режиме, но Вы также можете сделать это самостоятельно. Например, дистрибутивы Linux часто предоставляют контрольные суммы, чтобы Вы могли проверить правильно загруженный ISO-образ Linux, прежде чем записывать его на диск или помещать на USB-накопитель. Вы также можете использовать контрольные суммы для проверки целостности любого другого типа файла, от приложений до документов и носителей. Вам просто нужно знать контрольную сумму исходного файла.
В чем разница между хешами MD5, SHA-1 и SHA-256
Контрольные суммы — это полезный способ убедиться, что в файле нет ошибок. Если ошибка возникает из-за проблем с загрузкой или проблем с жестким диском, результирующая контрольная сумма будет другой, даже если это небольшая ошибка.
Однако эти криптографические хеш-функции несовершенны. Исследователи безопасности обнаружили «коллизии» с функциями MD5 и SHA-1. Другими словами, они обнаружили два разных файла, которые производят один и тот же хэш MD5 или SHA-1.
Это вряд ли произойдет случайно, но злоумышленник может использовать эту технику, чтобы замаскировать вредоносный файл. Вот почему не следует полагаться на суммы MD5 или SHA-1 для проверки подлинности файла — только для проверки на наличие повреждений.
Сообщений о конфликте SHA-256 пока не поступало, поэтому приложения теперь создают суммы SHA-256 вместо сумм MD5 и SHA-1. SHA-256 — более сильный и безопасный алгоритм.
Различные алгоритмы контрольной суммы дают разные результаты. Файл будет иметь разные контрольные суммы MD5, SHA-1 и SHA–256. Если Вам известна только сумма MD5 исходного файла, Вы должны вычислить сумму MD5 своей копии, чтобы проверить, совпадает ли она.
Как рассчитать контрольную сумму
Если Вы знаете контрольную сумму исходного файла и хотите проверить ее на своем компьютере, Вы можете легко это сделать. Windows, macOS и Linux имеют встроенные утилиты для генерации контрольных сумм. Вам не нужны сторонние утилиты.
В Windows команда PowerShell Get-FileHash вычисляет контрольную сумму файла. Чтобы использовать ее, сначала откройте PowerShell. В Windows 10 щелкните правой кнопкой мыши кнопку «Пуск» и выберите «Windows PowerShell». Вы также можете запустить его, выполнив поиск в меню «Пуск» по запросу «PowerShell» и щелкнув ярлык «Windows PowerShell».
Get-FileHash входит в состав Windows 10. Но в Windows 7 Вам необходимо установить обновление PowerShell 4.0.
В командной строке введите Get-FileHash и нажмите клавишу пробела.
Введите путь к файлу, для которого Вы хотите вычислить контрольную сумму. Или, чтобы упростить задачу, перетащите файл из окна проводника в окно PowerShell, чтобы автоматически указать путь к нему.
Нажмите Enter, чтобы запустить команду, и Вы увидите хэш SHA-256 для файла. В зависимости от размера файла и скорости памяти Вашего компьютера процесс может занять несколько секунд.
Если Вам нужен другой тип контрольной суммы, добавьте соответствующую опцию -Algorithm в конец команды, например:
Сравните рассчитанную контрольную сумму с исходной. Не нужно смотреть слишком внимательно, так как будет большая разница в контрольной сумме, даже если в базовом файле будет только крошечная разница.
Если контрольная сумма совпадает, файлы идентичны. Если нет, значит проблема — возможно, файл поврежден или Вы просто сравниваете два разных файла. Если Вы скачали копию файла и ее контрольная сумма не соответствует ожидаемой, попробуйте загрузить файл еще раз.
Контрольные суммы что это
Контрольная сумма файла используется для проверки оригинальности и целостности файла.
Например с помощью контрольных сумм мы проверяли оригинальность скаченных образов в этих статьях:
О контрольной сумме файла из википедии:
Контро́льная су́мма — некоторое значение, рассчитанное по набору данных путём применения определённого алгоритма и используемое для проверки целостности данных при их передаче или хранении. Также контрольные суммы могут использоваться для быстрого сравнения двух наборов данных на неэквивалентность: с большой вероятностью различные наборы данных будут иметь неравные контрольные суммы. Это может быть использовано, например, для обнаружения компьютерных вирусов. Несмотря на своё название, контрольная сумма не обязательно вычисляется путём суммирования.
С точки зрения математики контрольная сумма является результатом хеш-функции, используемой для вычисления контрольного кода — небольшого количества бит внутри большого блока данных, например, сетевого пакета или блока компьютерногофайла, применяемого для обнаружения ошибок при передаче или хранении информации. Значение контрольной суммы добавляется в конец блока данных непосредственно перед началом передачи или записи данных на какой-либо носитель информации. Впоследствии оно проверяется для подтверждения целостности данных.
Популярность использования контрольных сумм для проверки целостности данных обусловлена тем, что подобная проверка просто реализуема в двоичном цифровом оборудовании, легко анализируется и хорошо подходит для обнаружения общих ошибок, вызванных наличием шума в каналах передачи данных.
Криптографическая функция MD5 уже почти не используется для определения контрольных сумм, так как оказалось, что для неё можно быстро создавать с помощью современных компьютеров два разных файла, имеющих разную длину в байтах, но одинаковые величины контрольных сумм, подсчитанных с помощью алгоритма MD5.
Использование термина сумма связано с тем, что на заре цифровой связи при байтовых передачах информационными были 7 бит, а восьмой — контрольный — рассчитывался как младший разряд сложения информационных.
Подсчет контрольной суммы файлов в windows.
Для операционных систем windows существует множество программ которые подсчитывают контрольную сумму.
Самой распространенной программой считается программа HashTab.
Скачать и использовать ее в не коммерческих целях можно совершенно бесплатно с официального сайта программы.
Если у вас Windows 10 — то этот функционал уже встроен в файловый менеджер.
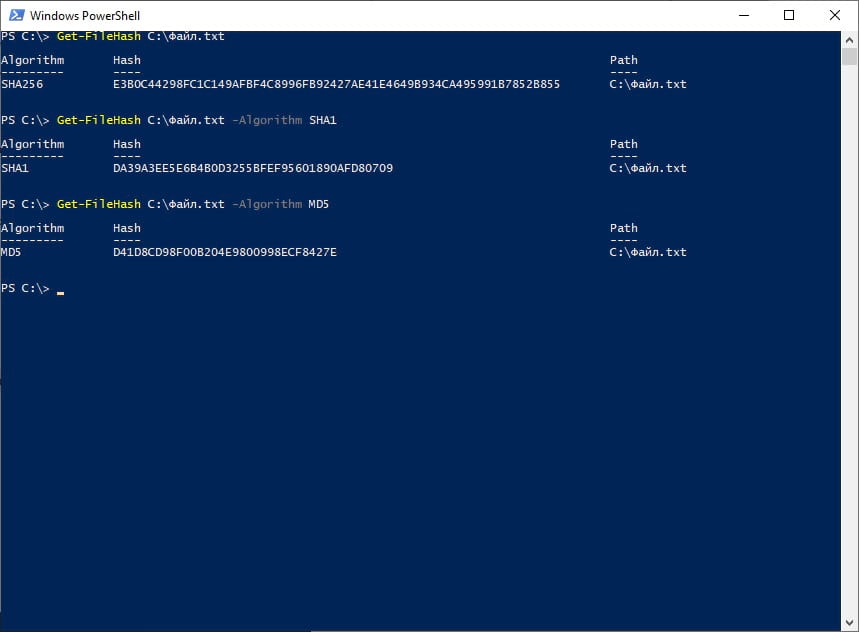
Кликаем по файлу правой кнопкой мыши, далее пункт CRC SHA и выбираем как посчитать контрольную сумму или выбираем пункт » * » который посчитает все возможные контрольные суммы из предоставленного списка.
Контрольная сумма файлов в Linux.
Подсчет контрольных сумм в linux осуществляется при помощи терминала.
Для подсчета MD5 суммы файла или строки, в Linux можно воспользоваться программой:
Для проверки контрольной суммы sha1:
Для проверки контрольной суммы sha256:
Для проверки контрольной суммы sha384:
Для проверки контрольной суммы sha512:
Для проверки контрольной суммы CRC:
Все эти программы входят в пакет coreutils — который должен быть предварительно установлен, например с помощью менеджера пакетов Sinaptic.
Для тех кто не любит терминал.
Можно установить расширение gtkhash для файлового менеджера и с помощью него производить все манипуляции.
Расширение есть для файловых менеджеров nautilus, nemo и thunar. Устанавливается через файловый менеджер Sinaptic.
После установки при выборе свойств файла появится вкладка в которой можно сравнить контрольную сумму или узнать ее.
Как то так. В комментариях добавляйте кто знает о других способах или использует другие методы.
Контрольная сумма файла: что это такое и как проверить
Скачивая файлы, программы или образы дисков вы наверняка замечали, что вместе с данными файлами часто распространяют и какие-то зашифрованные строки, которые называются контрольными или хеш суммами. В данной статье мы расскажем о том, что такое контрольная сумма, для чего ее используют и как проверить контрольную сумму для строк или файлов.
Что такое контрольная сумма
Контрольная сумма или хеш-сумма – это значение, которое было рассчитано по некоторому алгоритму на основе имеющихся файлов или данных. Особенностью контрольной суммы является то, что ее алгоритм, при одинаковых входных данных всегда выдает одинаковое значение. При этом малейшее изменение входных данных кардинально меняет значение контрольной суммы.
Эта особенность позволяет использовать контрольную сумму для проверки целостности файлов или данных. Например, вам нужно отправить какой-то файл, и вы хотите убедиться, что он не будет поврежден или изменен на своем пути к получателю. Для решения этой задачи можно использовать контрольную сумму. Высчитываете контрольную сумму и отправляете ее вместе с файлом. После чего получатель файла повторно высчитывает контрольную сумму файла и сравнивает ее с вашей контрольной суммой. Если значения совпадают, значит файл оригинальный, если нет, значит он получил какие-то изменения.
Также нужно упомянуть, что контрольную сумму нельзя использовать для получения исходных данных. То есть нельзя «расшифровать» хеш-сумму и получить данные которые были хешированы, хеш-сумму можно только сравнить с другой хеш-суммой. Это особенность открывает дополнительные возможности. Например, хеш-суммы используются для хранения паролей. Когда вы регистрируетесь на каком-то сайте и вводите свой пароль, то он не хранится на сервере в открытом виде. Вместо этого хранится только его контрольная сумма. А когда вы входите в свой аккаунт с использованием пароля, система получается ваш пароль, высчитывает его хеш-сумму и сравнивает с хеш-суммой, которая хранится на сервере. Если хеш-суммы совпали, значит пароль верный и вы можете войти в аккаунт, если хеш-суммы не совпадают, значит пароль не верный и вас перенаправляют на страницу для восстановления пароля.
Для высчитывания контрольной суммы существует множество различных алгоритмов или так называемых хеш-функций. Самыми известными и популярными алгоритмы являются: CRC32, MD5, SHA-1 и SHA-2. Но, есть и множество других алгоритмов, некоторые из которых имеют широкое применения, а некоторые используются только для специфических задач. При этом часть существующих алгоритмов признаны устаревшими или уязвимыми и больше не используются. Так, алгоритм MD5 практически полностью перестал использоваться поскольку выяснилось, что он может выдавать одинаковые значения для разных входных значений.
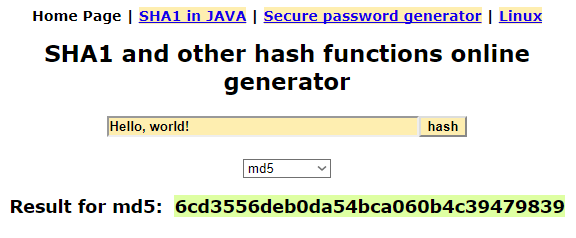
Для примера продемонстрируем, как выглядит контрольная сумма на практике. Например, возьмем строку «Hello, world!» и высчитаем ее контрольную сумму с использованием нескольких популярных алгоритмов.
Как видно, каждый алгоритм выдает значение, которое не имеет совершенно ничего общего с исходными данными. И сколько раз мы бы не высчитывали контрольную сумму строки «Hello, world!», мы каждый раз будем получать одни и те же значения.
Проверка контрольных сумм онлайн
Если нужно проверить контрольную сумму какой-то строки (например, пароля), то проще всего воспользоваться онлайн сервисами. Найти такие онлайн сервисы можно в любом поисковике по запросу «hash online».
Для примера рассмотрим сайт http://www.sha1-online.com. На этом сайте есть строка, в которую нужно ввести исходные данные, и выпадающий список, где нужно выбрать какой алгоритм вы хотите использовать для получения хеш-суммы.
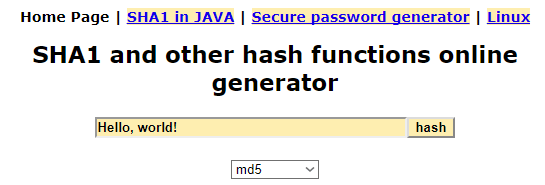
Чтобы проверить приведенную выше таблицу введем строку «Hello, world!», выберем алгоритм MD5 и нажмем на кнопку «hash».
В результате на экране появится строка со значением хеш-функции MD5.
Не сложно заметить, что полученное значение полностью совпадает с тем, которое указано в таблице выше, хотя данные из таблицы были получены другим способом.
Проверка контрольной суммы файла
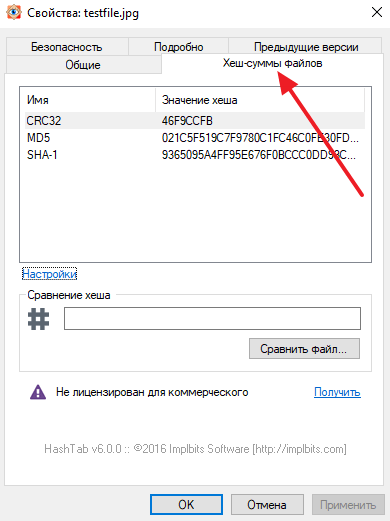
Если вам нужно проверить контрольную сумму файла (например, образа диска или программы), то вам понадобится специальная программа, которая умеет высчитывать контрольные суммы. Самой популярной программой такого рода является HashTab.
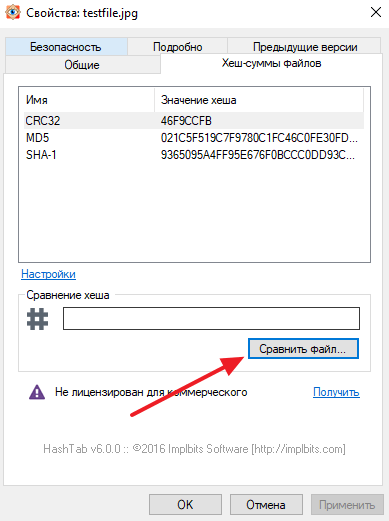
После установки данной программы в свойствах файла появится новая вкладка «Хеш-суммы файлов», в которой будет отображаться хеш-сумма выбранного вами файла.
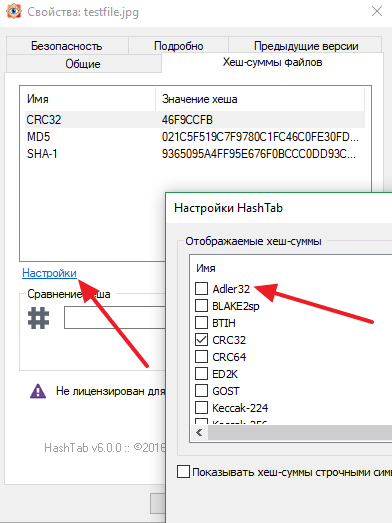
При этом пользователь можно изменить набор алгоритмов, которые программа HashTab использует для расчета хеш-суммы. Для этого нужно нажать на ссылку «Настройки», выбрать нужные алгоритмы и сохранить изменения с помощью кнопки «ОК».
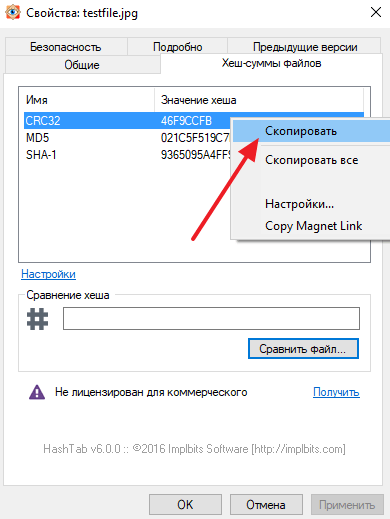
Полученные значения контрольных сумм можно скопировать, для этого нужно кликнуть на значению с помощью правой кнопки мышки.
Также HashTab позволяет сравнивать файлы. Для этого нужно нажать на кнопку «Сравнить файл» и выбрать другой файл.
Программа HashTab является бесплатной для личного пользования, некоммерческих организаций и студентов. Скачать программу можно на официальном сайте http://implbits.com/products/hashtab/.
Создатель сайта comp-security.net, автор более 2000 статей о ремонте компьютеров, работе с программами, настройке операционных систем.
Задайте вопрос в комментариях под статьей или на странице «Задать вопрос» и вы обязательно получите ответ.
Спасибо за статью. Все очень понятно изложено.
Зачем нужна контрольная сумма, если она по размерам больше чем то, что передают?
Простой расчет контрольной суммы
При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.
Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.
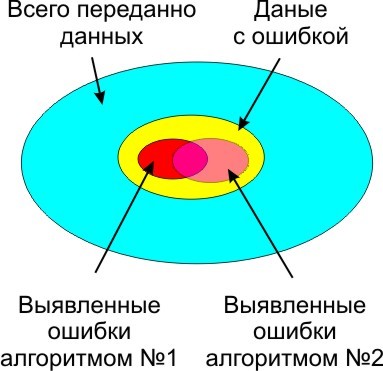
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.
Причина помех на физическом уровне, при передаче данных.
Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.
Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.
Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.
Бит четности (1-битная контрольная сумма)
На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:
Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.
8-битная контрольная сумма
Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично
Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:
.
,
на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:
Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).
Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.
Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.
Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.
Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:
Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:
Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов
Результат 91% от теоретического предела. Вполне годится для применения.
Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.
На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.
Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.
Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:
Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.
Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).
Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:
Результат 100.6% от теоретического предела.
Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:
Результат 86% от теоретического предела.
В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).
Небольшое улучшение в некоторых случаях дает так же:
16-битная контрольная сумма
Далее, предположим что нам мало 8 бит для формирования контрольной суммы.
Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.
Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.
Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.
Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.
Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.
32-битная контрольная сумма
Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения
За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:
Результат, из 10 млн. итераций ошибка обнаружена 3 раза
Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.
Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.
Вариант без умножения:
Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.
64-битная контрольная сумма
Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:
Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 🙂
Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.
Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.
Комментарии
В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.
Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.
Мой проект по исследованию CRC на гитхаб.
Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.