Коническая проекция что это
Коническая проекция
В конической проекции изображение строится на боковой поверхности конуса, секущего земной шар по двум параллелям или касательного к нему. Вершина конуса лежит на продолжении земной оси.
Параллели нормальной сетки являются дугами концентрических окружностей, а меридианы — их радиусами, углы между которыми пропорциональны соответствующим разностям долгот.
Искажения не зависят от долготы.
В равноугольной конической проекции меридианы сетки растянуты в такой же степени, в какой растянуты ее параллели.
Ссылки
Полезное
Смотреть что такое «Коническая проекция» в других словарях:
коническая проекция — Картографическая проекция, в которой параллели изображаются дугами концентрических окружностей, а меридианы – прямыми, расходящимися из общего центра параллелей, углы между которыми равны разностям их долгот. → Рис. 67 … Словарь по географии
коническая проекция — kūginė projekcija statusas T sritis fizika atitikmenys: angl. conic projection; conical projection vok. Kegelprojektion, f; konische Projektion, f rus. коническая проекция, f pranc. projection conique, f … Fizikos terminų žodynas
коническая картографическая проекция — коническая проекция Картографическая проекция, в которой параллели нормальной сетки дуги концентрических окружностей, а меридианы их радиусы, углы между которыми пропорциональны соответствующим разностям долгот. [ГОСТ 21667 76] Тематики… … Справочник технического переводчика
Проекция Альберса — … Википедия
Равновеликая проекция — Равновеликая проекция. Равновеликая проекция один из основных типов картографических проекций. Не искажает площадей и сохраняет на всей карте единый масштаб площадей, благодаря чему площади фигур на карте пропорциональны площадям… … Википедия
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — отображение всей поверхности земного эллипсоида или какой либо ее части на плоскость, получаемое в основном с целью построения карты. К. п. чертят в определенном масштабе. Уменьшая мысленно земной эллипсоид в Мраз, получают его геометрич. модель… … Математическая энциклопедия
легенда к географическим картам — НАСЕЛЕННЫЕ ПУНКТЫ :: более 1 млн. жителей :: от 250 тыс. до 1 млн. жителей :: от 100 тыс. до 250 тыс. жителей :: менее 100 тыс. жителей Прописными буквами выделены столицы. ПУТИ СООБЩЕНИЯ :: Железные дороги … Географическая энциклопедия
Карты географические — (истор.) Первоначальное понятие о К. можно встретить даже у дикарей, особенно живущих по берегам и о вам и имеющих более или менее ясное представление об окружающих их территорию местностях. Путешественники, расспрашивавшие эскимосов С. Америки и … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Картографическая коническая проекция: характеристики, достоинства, недостатки
Содержание:
В конических проекциях поверхности Земли меридианы становятся радиальными линиями с центром в вершине и равным угловым интервалом, а параллели Земли становятся дугами окружности, концентричными по отношению к вершине.
На рисунке 1 видно, что коническая проекция не позволяет представить оба полушария. Кроме того, ясно видно, что расстояния искажены в сторону от параллелей, пересекающих конус.
По этим причинам этот тип проекции используется для представления регионов средних широт, протяженных с востока на запад и меньшей протяженности с севера на юг. Так обстоит дело в континентальной части Соединенных Штатов.
Преимущество
Землю можно аппроксимировать сферой с радиусом 6378 км, учитывая, что все массы суши и воды находятся на этой большой сфере. Речь идет о преобразовании этой поверхности, которая покрывает объект в трех измерениях, например, сферу, в другой объект в двух измерениях: плоскую карту. Это приносит недостаток, заключающийся в том, что криволинейная поверхность искажается при ее проецировании на плоскость.
Картографические проекции, такие как коническая проекция, пытаются решить эту проблему с минимальной потерей точности. Следовательно, есть несколько вариантов построения проекции в зависимости от характеристик, которые вы хотите выделить.
Транспортировать глобус повсюду непросто, так как он занимает много места. Также невозможно увидеть всю поверхность Земли сразу, и невозможно воспроизвести все детали на масштабной модели.
Возможны следующие варианты проецирования:
— Проецировать на самолет или
— На цилиндре, который может разворачиваться в прямоугольную плоскость.
— Наконец-то на конусе.
Преимущество конической системы проецирования состоит в том, что она точна по сравнению с параллелями, выбранными для пересечения конуса.
Кроме того, он сохраняет ориентацию по меридианам практически неизменной, хотя может немного исказить шкалу по меридианам для широт, далеких от стандартных или опорных параллелей. Вот почему он подходит для представления очень больших стран или континентов.
Эквидистантная коническая проекция
Это коническая проекционная система, первоначально использовавшаяся Птолемеем, греческим географом, жившим между 100-170 годами нашей эры. Позже в 1745 году его улучшили.
Часто используется в атласах регионов с промежуточными широтами. Он подходит для отображения областей с несколькими градусами широты, принадлежащих одному из экваториальных полушарий.
В этой проекции расстояния истинны по меридианам и по двум стандартным параллелям, то есть параллелям, выбранным для пересечения с конусом проекции.
В эквидистантной конической проекции точка на сфере проходит радиально до пересечения с касательным или секущим конусом, принимая центр сферы за центр проекции.
Недостатки
Основным недостатком конической проекции является то, что она неприменима к экваториальным областям.
Кроме того, коническая проекция не подходит для картографирования больших регионов, а скорее отдельных областей, таких как Северная Америка.
Коническая проекция Альберта
Используйте две стандартные параллели и сохраните площадь, но не масштаб и форму. Этот тип конического выступа был введен Х. К. Альберсом в 1805 году.
Все области на карте пропорциональны земным. В ограниченных регионах направления относительно точны. Расстояния соответствуют расстояниям от сферической поверхности на стандартных параллелях.
В Соединенных Штатах эта система проекции используется для карт, показывающих границы штатов Союза, для которых 29,5º с.ш. и 45,5º с.ш. выбраны в качестве стандартных параллелей, что приводит к максимальной ошибке шкалы в 1, 25%.
Карты, сделанные с помощью этой проекции, не сохраняют углы, соответствующие углам сферы, а также перспективу или равноудаленность.
Конформная коническая проекция Ламберта
Он был предложен в 1772 году одноименным швейцарским математиком и географом. Его основная характеристика заключается в том, что он использует касательный или секущий конус к сфере, а проекция сохраняет неизменными углы. Эти качества делают его очень полезным в аэронавигационных картах.
Геологическая служба США (USGS) использует проекцию конуса Ламберта. В этой проекции расстояния истинны по стандартным параллелям.
В конической проекции Ламберта направления остаются достаточно точными. Области и формы слегка искажаются в положениях, близких к стандартным параллелям, но изменение формы и площади увеличивается с расстоянием между ними.
Поскольку целью этой проекции является поддержание направлений и углов, равных исходным на сфере или эллипсоиде, не существует геометрического метода их получения, в отличие от эквидистантной проекции Птолемея.
Скорее, это метод аналитического проектирования, основанный на математических формулах.
Базовые карты USGS для 48 континентальных штатов используют 33º и 45º с.ш. в качестве стандартных параллелей, что дает максимальную ошибку карты в 2,5%.
Для навигационных карт на Аляске используются базовые параллели: 55 ° и 65 °. Вместо этого в национальном атласе Канады используются 49º и 77º северной широты.
Ссылки
5 измерений устойчивости и их характеристики
Конические проекции.
Основные виды картографических проекций.
В авиации карты используются как при подготовке к полету, так и в процессе полета. При подготовке к полету карта необходима для прокладки и изучения маршрута полета; измерения путевых углов и расстояний между пунктами маршрута; определения географических координат пунктов; нанесения точек расположения радиотехнических средств, обеспечивающих полет; получения данных о магнитном склонении в районе полета; изучения рельефа местности.
В полете карта применяется для ведения визуальной и радиолокационной ориентировки; контроля пути и прокладки линий положения самолета; определения навигационных элементов полета.
Карты нужны также службе движения для руководства полетами и контроля за их выполнением. Авиационные карты создаются в определенных картографических проекциях.
Картографической проекцией называется способ изображения земной поверхности на плоскости. Сущность любой картографической проекции состоит в том, что поверхность земного шара переносится сначала на глобус определенного размера, а затем с глобуса по намеченному способу на плоскость.
При переносе поверхности Земли с глобуса на плоскость приходится в одних местах растягивать изображения, а в других сжимать, т.е. допускать искажения. Каждая проекция имеет определенную степень искажения длин, направлений и площадей и определенный вид сетки меридианов и параллелей. Выбор проекции для построения карты зависит от того, каким требованиям должна отвечать данная карта.
По виду сетки меридианов и параллелей все картографические проекции делятся на конические (поликонические) цилиндрические, и азимутальные.
Конические проекции.
Конические проекции могут строиться на касательном или секущем конусе.
В зависимости от расположения оси конуса относительно оси вращения глобуса конические проекции могут быть нормальные, поперечные и косые. Большинство авиационных карт конической проекции построено в нормальной равноугольной проекции на касательном или секущем конусах.
Равноугольная коническая проекция на касательном конусе. Построение этой проекции (рис. 1) наглядно можно объяснить следующим образом. Все меридианы выпрямляют до соприкосновения с боковой поверхностью конуса. При этом все параллели, кроме параллели касания, будут растягиваться до размеров окружности конуса. Для того чтобы сделать проекцию равноугольной и сохранить подобие фигур,
Рисунок 1. Равноугольная коническая проекция на касательном конусе
производят растягивание меридианов в такой степени, в какой были растянуты параллели в данной точке карты. Затем конус разрезается по образующей и разворачивается на плоскость. Карты в равноугольной конической проекции на касательном конусе имеют следующие свойства:
— меридианы изображаются в виде прямых, сходящихся к полюсу;
— угол схождения меридианов определяется по формуле
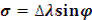
— параллели имеют вид дуг концентрических окружностей, расстояния между которыми увеличиваются по мере удаления от параллели касания;
— на параллели касания искажения длин отсутствуют, а в полосе ±5° от этой параллели они незначительны и в практике не учитываются;
— локсодромия изображается кривой линией, обращенной своей выпуклостью к экватору;
— ортодромия для расстояний до 1200 км изображается прямой линией, а для больших расстояний имеет вид кривой, обращенной своей выпуклостью в сторону более крупного масштаба.
В равноугольной конической проекции на касательном конусе издаются бортовые карты масштабов 1:2000000; 1:2500000; 1:3000000; 1:4000000 и обзорная карта масштаба 1:5000000.
Рисунок 2. Равноугольная коническая проекция на секущем конусе
Справка
Самая простая коническая проекция проходит по касательной к глобусу вдоль линии широты. Эта линия называется стандартной параллелью. Меридианы проецируются на коническую поверхность, сходясь на вершине или в точке конуса. Параллели проецируются на коническую поверхность как кольца. Конус затем “рассекается” вдоль любого меридиана для создания конечной конической проекции, в которой имеются прямые сходящиеся меридианы и параллели, представленные концентрическими окружностями. Меридиан, противолежащий линии сечения, становится центральным меридианом.
В целом, чем дальше от стандартной параллели, тем больше искажение. Соответственно, отсечение верхушки конуса создает более точную проекцию. Этого можно достичь, если не использовать полярную область при проецировании объектов. Конические проекции используются для среднеширотных зон, имеющих ориентацию с востока на запад.
Более сложные конические проекции соприкасаются с поверхностью глобуса в двух местах. Эти проекции называются секущими коническими проекциями и определяются двумя стандартными параллелями. Можно также определить секущую проекцию с помощью одной стандартной параллели и коэффициента масштабирования. Характер искажений при секущих проекциях различается для районов, расположенных между стандартными параллелями, и для районов, расположенных за их пределами. Как правило, секущая проекция дает меньшее суммарное искажение, чем касательная проекция. В еще более сложных конических проекциях ось конуса не совпадает с полярной осью глобуса. Такие проекции называются косыми.
Изображение географических объектов зависит от расстояния между параллелями. При их равном удалении друг от друга проекция получается равнопромежуточной в направлении с севера на юг, но не равноугольной и не равновеликой. Примером такого типа проекций является Равнопромежуточная Коническая проекция. Для небольших областей общее искажение минимально. В равноугольной конической проекции Ламберта расстояние между центральными параллелями меньше, чем у параллелей ближе к границам, и не искажаются формы малых географических объектов на мелкомасштабных и крупномасштабных картах. В равновеликой конической проекции Альберса параллели вблизи северного и южного полюса расположены ближе друг к другу, чем центральные параллели, и проекция отображает эквивалентные площади.
НАВИГАЦИЯ. Глава 3. §19 Классификация картографических проекций.
§19 Классификация картографических проекций.
Картографические проекции можно классифицировать по различным признакам. Однако с точки зрения построения и практического использования карт, наиболее употребительными признаками их классификации служат:
• характер искажений проекций, обусловливающий возможности практического использования карт;
• вид меридианов и параллелей нормальной сетки.
По характеру искажений
все картографические проекции делятся на четыре группы:
• равноугольные, или конформные;
• равновеликие, или эквивалентные (равноплощадные);
Равноугольные проекции
Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли.
Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом.
Однако, при сохранении неискаженными углов и направлений, в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.
Постоянство частного масштаба в данной точке по всем направлениям облегчает производство измерений на карте, составленной в равноугольной проекции. Для учета изменения масштаба при измерении больших отрезков их следует измерять на карте по частям.
Свойство конформности позволяет на картах, составленных в таких проекциях, измерять углы и азимуты непосредственно с помощью транспортира. Эти свойства обусловили широкое применение равноугольных проекций для построения морских карт. Отметим, что равноугольные проекции сохраняют равными углы, но не кривизну линий, поэтому подобие сохраняется только для малых фигур.
К равноугольным проекциям относятся проекции Меркатора, Гаусса, стереографическая и некоторые другие.
Равновеликие проекции
Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте.
Бесконечно малый на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.
На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.
Равнопромежуточные проекции
Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений.
Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга.
Произвольные проекции
Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными.
К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.
По виду меридианов и параллелей нормальной картографической сетки
проекции делятся на следующие основные группы:
Из всех перечисленных здесь рассматриваются лишь те виды проекций, которые используются или могут использоваться для построения морских карт.
Конические проекции
Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов.
Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса.
Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса. т. е. меньше главного масштаба.
Азимутальные проекции
Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов
Из приведенного определения видно, что азимутальные проекции являются частным случаем конических проекций.
Точка схождения меридианов в азимутальных проекциях является изображением полюса нормальной системы координат. Свойствами азимутальных проекций являются: равноугольность, равновеликость или равнопромежуточность.
К классу азимутальных проекций относятся перспективные проекции, получающиеся путем проектирования точек поверхности глобуса (шара) на картинную плоскость лучами, исходящими из постоянной точки.
Эта точка называется точкой зрения.
Картинная плоскость может или касаться поверхности проектируемого глобуса, или находиться от него на некотором удалении, или пересекать ее. Точка зрения выбирается на перпендикуляре к картинной плоскости, проходящем через центр проектируемого глобуса.
В зависимости от расположения точки зрения относительно центра глобуса перспективные проекции делятся:
— на ортографические, когда точка зрения удалена в бесконечность;
— на внешние, когда точка зрения находится на конечном расстоянии от центра проектируемого глобуса, но далее точки, представляющей антипод полюса нормальной системы координат;
— на стереографические, когда расстояние от центра глобуса до точки зрения равно радиусу глобуса, т.е. когда точка зрения помещается в точке шара, противоположной полюсу нормальной системы координат (в точке — антиподе полюса нормальной системы координат);
— на центральные (гномонические), когда точка зрения помещена в центре глобуса.
Цилиндрические проекции
Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми.
Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.
Общие уравнения цилиндрических проекций имеют вид:
x = f (φ); y = C λ
Вид функции x = f (φ) и коэффициент С определяют важнейшие свойства цилиндрической проекции. Изменяя их, можно получить равноугольную, равнопромежуточную, равновеликую или произвольную проекцию. Цилиндрические проекции могут быть получены путем проектирования поверхности глобуса на касательный или секущий глобус цилиндр. При проектировании на касательный по экватору цилиндр масштаб вдоль экватора сохраняет равенство главному масштабу, т.е. экватор глобуса изображается на проекции без искажений. При проектировании на секущий цилиндр линиями нулевых искажений будут являться параллели сечения.
Из цилиндрических наиболее употребительны в кораблевождении прямая и поперечная проекции Меркатора и поперечная проекция Гаусса.