Коэффициент возвращающего момента в чем измеряется
Лекция 4. Физика колебаний. Гармонический осциллятор. Нормальные моды
Дифференциальное уравнение гармонических колебаний и его решение. Модель гармонического осциллятора. Примеры гармонических осцилляторов: физический, математический и пружинный маятники. Определение их периодов и частот. Свободные колебания. Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний: коэффициент затухания, декремент, логарифмический декремент затухания, добротность. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс. Параметрический резонанс.
4.1. Дифференциальное уравнение гармонических колебаний и его решение
Воспользовавшись основным уравнением классической динамики (уравнением второго закона Ньютона) можно получить уравнение движения материальной точки (тела), совершающего гармоническое колебание:
F= ma или F = ma, (4.1)
F = åFi— результирующая сила, под действием которой совершается гармоническое колебание (возвращающая сила);
Из уравнения (4.2) видно, что сила, под действием которой совершается гармоническое колебание, пропорциональна смещению и направлена в сторону противоположную ему. Она называется возвращающей силой. Возвращающая сила стремится вернуть материальную точку в положение равновесия.
Таким образом, уравнение движения материальной точки при гармоническом колебательном движении имеет вид

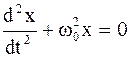
Решая дифференциальное уравнение гармонического колебательного движения, можно получить значение, например, периода колебаний, собственной частоты.
4.2. Примеры гармонических осцилляторов. Физический, математический и пружинный маятники.
Определение их периодов и частот
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида (4.3):

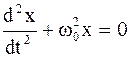
Колебания гармонического осциллятора являются примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики.
В качестве примеров гармонических осцилляторов рассмотрим гармонические колебания систем, называемых пружинным, физическим и математическим маятниками.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В векторной форме



M=[r´F].
Главный или результирующий момент сил относительно неподвижной оси вращенияравен векторной сумме моментов слагаемых сил:
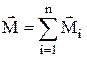
Моменты сил относительно осей, которые перпендикулярны и параллельны оси вращения, равны нулю.
Основной закон динамики вращательного движения твердых (недеформирующихся) тел, для которых I=const (второй закон динамики для вращательного движения):
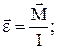
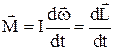
Импульс вращающего момента – произведение вращающего момента на время его действия:
M×dt = dL.
Осциллятор– физическая система, совершающая колебания; система, у которой величины, описывающие ее, периодически меняются с течением времени.
Гармонический осциллятор– механическая система, совершающая колебания около положения устойчивого равновесия, описывающие величины которой изменяются по гармоническому закону (закону синуса или косинуса).
Уравнение движения гармонического осциллятора:
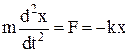
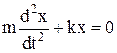
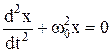
где a = d 2 x/dt 2 = –ω0 2 x – ускорение материальной точки;
F – возвращающая сила, которая стремится вернуть систему в положение равновесия (F = –mω0 2 x = –kx);
k = mω0 2 – коэффициент возвращающей силы. Он численно равен возвращающей силе, вызывающей единичное смещение.
Решение уравнения движения гармонического осциллятора:
Уравнение гармонических колебаний в комплексном виде:
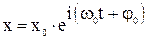
В теории колебаний принимается, что величина x равна вещественной части комплексного выражения, стоящего в этом выражении справа.
Дифференциальное уравнение гармонического колебательного движения:
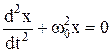
Решением дифференциального уравнения гармонических колебанийявляется выражение вида
где k = m w0 2 – коэффициент возвращающей силы;
x – смещение материальной точки;
x0 – амплитуда колебаний;
w0 = 2p/Т = 2pn – круговая (циклическая частота);
n = 1/T – частота колебаний;
T – период колебаний;
j0 – начальная фаза колебаний.
Примеры гармонических осцилляторов:
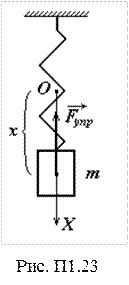
а) пружинный маятник – тело массой m (рис. П1.23), подвешенное на пружине, совершающее гармоническое колебание.
Упругие колебания совершаются под действием упругих сил:
где k = m wo 2 – коэффициент жесткости;
Dl – относительное удлинение.
Уравнение движения пружинного маятника:
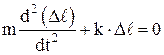
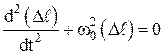
где 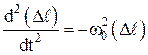
Dl – величина деформации.
Решение уравнения движения пружинного маятника:
Круговая частота, частота и период колебаний пружинного маятника:
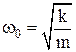
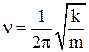
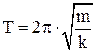
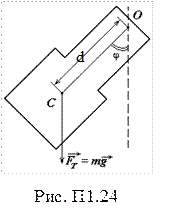
б) физический маятник – твердое тело, совершающее гармоническое колебательное движение относительно оси, не совпадающей с центром масс (рис. П1.24).
Уравнение движения физического маятника:
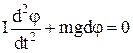
Решение уравнения движения физического маятника:
где α – начальная фаза колебаний.
Круговая частота, частота и период колебаний физического маятника:
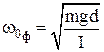
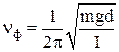
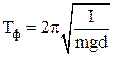
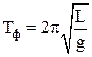
где L = I/md – приведенная длина физического маятника – длина такого математического маятник, период колебаний которого равен периоду колебаний физического маятника;
I – момент инерции физического маятникa относительно оси колебаний;
m – масса физического маятника;
d – расстояние между осью колебаний и центром масс;
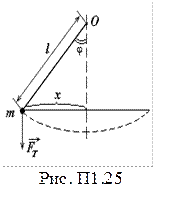
в) математический маятник – тело массой m, размерами которого можно пренебречь, подвешенное на невесомой, нерастяжимой нити (рис. П1.25).
Круговая частота, частота и период колебаний математического маятника:
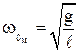
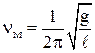
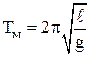
Приведенная длина физического маятника – величина, численно равная длине такого математического маятника, период колебаний которого равен периоду колебаний физического маятника:
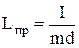
Крутильные колебания – колебания, совершающиеся под действием закручивающего момента, пропорционального углу закручивания (колебания диска, подвешенного на стальной нити):
где 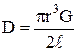
Методика определения коэффициента возвращающей силы пружины



Часть 1 Определение коэффициента возвращающей силы пружины.
1. Подвесить на штатив пружину с подвеской и заметить по указателю длину ненагруженной пружины 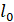
2. Положить на подвеску грузик массой m = 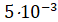
4. Рассчитать по формуле (4.30) коэффициент возвращающей силы для пяти измерений и найти среднее значение коэффициента.
5. Определить отклонение от среднего отдельных измерений
Δ 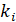
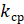
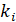
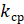
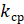
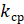
Таблица 4.2 – Результаты измерений и вычислений
Часть 2 Определение периода колебаний нагруженной пружины
1. Поместить на подвеску два грузика и записать массу грузиков с подвеской и указателем 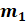
2. Слегка приподнять груз на пружине (на 6–8 мм), отпустить ее и, пропустив 5–6 колебаний, отсчитать по секундомеру время, за которое пружина совершит N колебаний (количество колебаний N задает преподаватель). По формуле 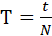
3. Опыт повторить 3 раза (число N можно взять разное), рассчитать каждый раз период и найти средний период 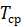
4. На подвеску добавить еще три грузика, подсчитать новую общую массу грузов и подвески 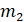
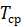
5. Используя формулу (4.32), найти теоретические значения периодов нагруженной пружины, взяв за коэффициент упругости значение 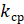

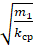
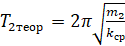
6. Приняв полученные значения 

δT
7.Данные измерений и вычислений занести в таблицу 4.3.
Таблица 4.3 – Результаты измерений и вычислений
| Масса, кг | № опыта | N | 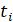 , с , с | 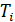 , с , с | 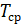 , с , с | 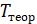 , с , с | δT, % |
| 2 | 14 | 16,3 | |||||
| 3 | 16 | 18,5 |
8. Окончательные результаты измерений для k записать в виде:
k= ( 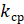
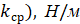
Контрольные вопросы
1. Напишите уравнение гармонического колебания. Что называется гармоническим колебанием?
2. Дайте определение величин, характеризующих гармоническое колебание
(амплитуда, фаза, частота, циклическая частота, период).
3. По каким формулам определяется ускорение колеблющейся точки?
4. Какие силы вызывают гармонические колебания? Каковы их свойства?
5. Какова природа возвращающей силы в данной работе? Какая формула ее определяет?
6. Что такое коэффициент возвращающей силы? По каким формулам его определяют?
7. Как можно рассчитать период колебаний нагруженной пружины? От чего он зависит?
Как можно практически измерить период колебаний груза на пружине?
3. Как в работе измеряется расстояние между центром диска и осью отверстия?
ЛАБОРАТОРНАЯ РАБОТА № 1
Экспериментальное определение момента инерции вращающейся системы Цель работы: измерение и теоретический расчет момента инерции системы тел и изучение вращательного движения твердого тела.
Методика измерений Маятник Максвелла (рис.2.8) представляет собой диск, жестко посаженный на стержень и подвешенный на двух параллельных нитях (бифилярный подвес).
J 2 mv 2 mgh mgh 0, (2.41)
Экспериментальная установка Общий вид экспериментальной установки показан на рис.2.10.
На вертикальной стойке 12 основания 1 крепятся два кронштейна:
верхний 2 и нижний 3. Верхний кронштейн снабжен электромагнитами 13 и устройством 4 для крепления и регулировки бифилярного подвеса
5. Маятник представляет собой диск 6, закрепленный на стержне 7, подвешенном на двух нитях. На диске крепятся сменные кольца 8.
Масса сменных колес 8 указана на каждом кольце. Маятник со сменными кольцами фиксируется в верхнем исходном положении с помощью электромагнита.
На вертикальной стойке нанесена миллиметровая шкала 14, по которой определяется ход маятника.
Фотоэлектрический датчик 9 закреплен на кронштейне 3.
Фотодатчик 9 предназначен для выдачи электрических сигналов на миллисекундомер 10, который является прибором для измерения времени.
1. Сформулируйте закон сохранения энергии для движения маятника.
2. Как определяется момент инерции маятника?
3. Как теоретически подсчитывают момент инерции диска и чему он равен?
4. Для чего в опытах используется электромагнит?
5. Какая существует связь между моментом силы и угловым ускорением для равноускоренного движения диска, момент инерции которого J?
ЛАБОРАТОРНАЯ РАБОТА №
Изучение динамики вращательного движения Цель работы: изучение основного уравнения динамики вращательного движения твердого тела и определение момента инерции тел.
Экспериментальная установка Общий вид маятника изображен на рис.2.12. На вертикальной стойке крепятся три кронштейна: верхний 2, средний 3 и нижний 4.
Положение всех кронштейнов на вертикальной стойке строго зафиксировано.
На верхнем кронштейне 2 крепится блок 5 изменения направления движения эластичной нити 6, на которой подвешен крючок 7 с грузами
8. Вращение блока 5 осуществляется в узле подшипников 19, который дает возможность уменьшить трение.
На среднем кронштейне 3 крепится электромагнит 14, который удерживает систему с грузами в неподвижном состоянии. На этом же кронштейне расположен узел подшипников 9, на оси которого с одной стороны закреплен двухступенчатый шкив 13, на котором имеется приспособление для закрепления нити 6. На другом конце оси находится крестовина 10, представляющая собой четыре металлических стержня с нанесенными на них рисками через каждые 10 мм, закрепленных в бобышке 12 под прямым углом друг к другу.
На каждом стержне могут свободно перемешаться и фиксироваться грузы 11, что дает возможность ступенчатого изменения момента инерции крестовины маятника. На нижнем кронштейне 4 крепится фотоэлектрический датчик 15, который выдает электрический сигнал на миллисекундомер 16 для окончания счета промежутков времени. На этом же кронштейне крепится резиновый амортизатор 17, о который ударяется груз при остановке.
Маятник снабжен миллиметровой линейкой 18, по которой определяется начальное и конечное положение грузов, а следовательно, и пройденный путь. Миллисекундомер 16 с цифровой индикацией времени закреплен на основании 1.
12. Найти момент силы трения М тр ( М тр равен координате точки пересечения графика с осью М) (рис.2.14).
13. Проделать те же измерения для шкива другого радиуса (r2 = см) и снова определить J и М тр. Результаты измерений занести в табл.2.5.
14. Выключить установку, нажав на кнопку “Сеть”.
15. Рассчитать доверительную и относительную погрешность результата измерений момента инерции для одной серии опытов.
1. Напишите закон сохранения энергии применительно к данной работе.
2. Получите формулу для расчета вращающего момента М.
3. Что такое центр тяжести?
4. Чему равен момент сил тяжести всех частиц тела относительно любой горизонтальной оси, проходящей через центр тяжести?
ЛАБОРАТОРНАЯ РАБОТА № 6
Определение момента инерции тела и скорости полета “пули” Цель работы: изучение динамики вращательного движения твердого тела с помощью крутильного маятника.
Рассмотрим вращательное движение маятника после удара.
Пренебрегая трением, можно применить для данного этапа закон сохранения механической энергии. Тогда кинетическая энергия маятника сразу после удара равна потенциальной энергии упругой деформации проволок в момент максимального отклонения маятника:
— масса груза (рис.2.16).
Экспериментальная установка Общий вид установки показан на рис. 2.16.
Основным элементом установки является маятник. Он представляет собой горизонтальный стержень 7, закрепленный на вертикальной проволоке 6, натянутой между кронштейнами 5 установки. Вдоль стержня могут перемещаться два груза 3 массой m = 0,18 кг каждый.
Винты 4 служат для закрепления грузов в определенном положении.
На концах стержня находятся пластины 1, покрытые с одной стороны пластилином. На торце пластины находится вертикальная черта, которая служит индикатором для шкалы на прозрачном экране 2, закрывающем маятник, при определении положения и угла отклонения маятника от положения равновесия. На пластине имеются деления, показывающие расстояние от оси подвеса маятника. На самом стержне 7 нанесены поперечные штрихи на расстоянии 1 см друг от друга, первый на расстоянии 0,02 м от оси.
3. Зарядить “пистолет”:
а) сдвинуть ручки 9 вперед до упора;
б) Повернуть ручки 9 и поместить на стержень “пулю”;
в) Вернуть ручки 9 в горизонтальное положение и оттянуть их назад до щелчка.
4. Убедившись, что маятник неподвижен, произвести выстрел, наклонив ручки 9. Произвести отсчет максимального угла поворота маятника. Рассчитать угол отклонения маятника по формуле 1 = – 0.
5. Измерить по шкале маятника расстояние L от следа пули до оси маятника Z.
6. Повторить измерения п.п 2. 5 не менее 4-х раз.
7. Рассчитать среднее значение максимального угла отклонения маятника 1, как среднее арифметическое нескольких значений 1, и среднее значение расстояния L.
8. Установить грузы маятника на максимальном расстоянии друг от друга, измерить а2 по шкале маятника.
9. Произвести измерения по п.п 2. 4 не менее 4 раз и рассчитать угол отклонения маятника по формуле 2 = – 0.
10. Рассчитать среднее значение максимального угла отклонения 2 при данном положении грузов.
11. Измерить толщину груза h по шкале маятника и радиус грузов r при помощи штангенциркуля.
12. Рассчитать момент инерции маятника по формуле (2.65), подставляя полученные значения углов 1 и 2 в радианах.
13. Рассчитать доверительную и относительную погрешность результата.
Определение скорости полета пули
1. Измерить длины проволок l1 и l2 и их диаметры D1 = 2R1 и D2 = 2R2.
2. По формуле (2.59) рассчитать коэффициент возвращающего момента с.
3. Используя выражение (2.62), рассчитать момент инерции маятника с грузами J1. Данные, необходимые для расчета получены в первом упражнении, масса “пули” mп = 0.75 г.
4. По формуле (2.66) для средних значений L и 1 рассчитать среднюю скорость полета пули v (подставляя 1 в радианах).
5. Рассчитать доверительную и относительную погрешность определения скорости пули.
2. Записать формулы для кинетической энергии вращающегося тела и потенциальной энергии закрученной проволоки.
3. Что такое коэффициент возвращающего момента?
4. Как можно определить момент инерции маятника?
Вопросы по разделу 2
1. Кинематические характеристики вращательного движения тела.
2. Нормальное и тангенциальное ускорение тела.
3. Понятие момента силы относительно неподвижной точки.
Каковы единицы измерения момента силы?
4. Момент импульса относительно неподвижной точки. Уравнение моментов.
5. Закон сохранения момента импульса для системы материальных точек.
6. Понятие момента силы относительно оси.
7. Понятие момента импульса твердого тела относительно оси.
8. Написать основное уравнение динамики вращательного движения.
9. Что такое момент инерции тела? Каков его физический смысл?
10. Расчет момента инерции стержня относительно оси, проходящей через центр масс перпендикулярно стержню.
11. Расчет момента инерции диска относительно оси, проходящей через центр масс перпендикулярно плоскости диска.
12. Теорема Штейнера, пример ее применения.
13. Кинетическая энергия вращающегося тела.
14. Закон сохранения момента импульса для твердого тела, вращающегося относительно неподвижной оси.
РАЗДЕЛ
Механические колебания и волны
3.1 Незатухающие гармонические колебания. Маятники Колебаниями называются процессы, характеризующиеся той или иной степенью повторяемости во времени. По физической природе колебания могут быть механическими, электромагнитными и др.
Колебания называются периодическими, если значения физических величин, характеризующих состояние системы, повторяются через равные промежутки времени. Минимальный из этих промежутков называется периодом колебаний Т. За период колебаний совершается одно полное колебание. Число полных колебаний, совершаемых в единицу времени, называется частотой колебаний
Одной из простейших колебательных систем является легкая спиральная пружина, к которой подвешен груз массой m (рис.3.1). Если вывести груз из положения равновесия, немного растянув Fупр пружину, и предоставить ее самой себе, то на груз m будет действовать упругая (возвращающая) сила пружины, прямо пропорциональная смещению х и x x направленная в сторону, противоположную смещению: F kx ; коэффициент возвращающей силы k в этом случае часто называют жесткостью Рис. 3.1 пружины. Под действием силы F тело совершает собственные гармонические колебания, которые можно наблюдать при малом сопротивлении среды.
Напишем второй закон Ньютона применительно к поступательному колебательному движению груза на пружине
Из выражения амплитуды затухающих колебаний видно, что коэффициент затухания есть величина, обратная тому времени, за которое амплитуда убывает в е раз. Если = 0, уравнение (3.32) переходит в уравнение гармонических незатухающих колебаний (3.4).
Подставляя уравнение (3.32) в (3.31), находим значения коэффициента затухания и круговой частоты :
r ; (3.33) 2m. (3.34) Период затухающих колебаний
Продифференцировав подкоренное выражение по частоте и приравняв полученное соотношение нулю, найдем значение резонансной частоты
График зависимости амплитуды установившихся вынужденных колебаний от частоты вынуждающей силы представлен на рис.3.5 для двух значений коэффициента затухания. Чем меньше затухание, тем круче поднимается и опускается амплитудная кривая А =f( ) при резонансе.
3.4 Волны Волнами называются процессы распространения возмущений какой-либо физической величины, характеризующей состояние вещества или поля. Процесс распространения механических возмущений в упругой среде называется упругой волной.
Распространение упругих волн состоит в возбуждении колебаний все более и более удаленных от источника волн частиц среды.
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды совершают колебания вдоль направления распространения волны. В поперечной волне колебания частиц совершаются в направлениях, перпендикулярных к направлению распространения волны.
Кроме того, поперечные волны могут распространяться на поверхности жидкости. Скорость распространения упругой волны в среде равна скорости v распространения в ней небольших возмущений в виде упругой деформации.
Скорость распространения упругих поперечных волн в изотропных твердых средах G (3.45) vпопер,
Если распространяющееся возмущение упругой среды является гармоническими колебаниями с неизменной круговой частотой, то волна называется гармонической.
В частном случае, когда А1 = А2 в точках, определяемых условием (3.56), колебания гасят друг друга.
При всех других значениях разности фаз, отличных от целого, величина амплитуды имеет значение между А1 А2 и А1 +А2.
ЛАБОРАТОРНАЯ РАБОТА № 2
Измерение ускорения свободного падения с помощью математического и оборотного (физического) маятников Цель работы: изучение колебаний физического и математического маятников и измерение ускорения свободного падения.
J (3.61) Lпр ma будет иметь такой же период колебаний, что и данный физический маятник. Величину (3.61) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Для всякого тела, рассматриваемого как физический маятник, можно указать две такие точки, именуемые центрами качания, что период малых колебаний при качании вокруг осей, проходящих через эти точки одинаков, а расстояние между ними равно приведенной длине физического маятника. На этом свойстве оборотного маятника основано определение ускорения свободного падения.
Оборотным будет такой маятник, у которого имеются две параллельные друг другу, закрепленные опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов или опорных призм добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно Lпр. Измерив период колебаний маятника и зная Lпр, можно из формулы Lпр (3.62) T2 g найти ускорение свободного падения g.
Экспериментальная установка Для измерения ускорения свободного падения предназначена экспериментальная установка, общий вид которой приведен на рис.3.8.
Установка состоит из математического и оборотного маятников.
Математический маятник представляет собой металлический шарик 5 на бифилярном подвесе 4. Длина подвеса может изменяться в пределах (0,1 – 0,5) м вращением винта 3 и измеряется с помощью линейки 10, укрепленной на стойке 9.
Оборотный маятник состоит из металлического стержня 14, на котором крепятся две способные перемещаться опорные призмы 13, обращенные ножами навстречу друг другу, и два тяжелых чечевицеобразных груза 12, перемещение которых существенно изменяет распределение масс.
Установка снабжена фотодатчиком 11, фиксирующим прохождение маятником положения равновесия. Сигнал с датчика подается на миллисекундомер 7 и счетчик числа полных колебаний 8.
2 0.3 2 0.35 2 0.4 2 0.45 1 2 0.5
4. Установочными винтами 3 и 6 отрегулировать положение шарика так, чтобы он проходил между оптическими элементами фотодатчика.
5. Подключить установку к сети 220 В. Нажать кнопку “Сеть”.
6. Отклонить шарик на небольшой угол (5 – 10) и отпустить.
7. Нажать кнопку “Сброс” на панели секундомера и отпустить ее.
После n = (10 – 15) колебаний нажать кнопку “Стоп”. Показания миллисекундомера занести в табл.3.1.
8. Повторив п.п 6, 7 еще два раза, найти среднее значение периода.
9. Повторить п.п 2. 8 для длин маятника (35, 40, 45 и 50) см.
10. Выключить установку, нажав кнопку “Сеть”.
11. По этим данным построить график зависимости Т2 = f(L) (экспериментальные точки и прямая линия).
12. С использованием графика (прямой линии) определить ускорение свободного падения по формуле (3.57).
13. Подсчитать доверительную и относительную погрешность результата измерения.
4. Не изменяя положения грузов А и В, перевернуть маятник, подвесив его за призму 2, и аналогичным образом измерить период Т 2 при положении призмы 2 вблизи груза В. Число колебаний при этом может быть не очень велико. Убедиться, что теперь период меньше, чем Т1.
5. Измерить расстояние между ножами призм L.
6. Снять маятник со штатива и незначительно (не более чем на 1 см) переместить призму 2 ближе к центру стержня. Подвесить маятник за призму 2 и измерить период Т 2 и расстояние L.
7. Перемещая призму 2, найти два таких положения призмы, когда период колебаний несколько больше и несколько меньше периода Т1, и измерить эти периоды с достаточно высокой точностью ((10 – 20) колебаний).
Измерить соответствующие расстояния между ножами призм.
ЛАБОРАТОРНАЯ РАБОТА № 012 Изучение колебаний математического маятника и явления параметрического резонанса Цель работы: исследование закономерностей колебаний математического маятника и наблюдение явления параметрического резонанса.
Методика измерений Математический маятник можно представить как материальную точку, подвешенную на невесомой и нерастяжимой нити. На практике математическим маятником можно считать тяжелое тело, подвешенное на легкой нити, длина которой во много раз больше размеров тела.
Формулу (3.63) можно записать в виде:
Но возможны и другие варианты, например параметрическое возбуждение, когда внешняя периодическая сила действует не непосредственно на движение системы, а только изменяет с определенной частотой один из параметров системы.
Так если при колебаниях математического маятника (рис.3.11) с частотой в два раза большей, чем частота колебаний маятника, укорачивать подвес при прохождении положения равновесия (см. рис.3.11 положение 2) на некоторую величину и 1 3 удлинять нить подвеса на ту же величину при наибольшем отклонении (см. рис.3.11 положения 1 и 3), то амплитуда колебаний маятника увеличивается. Это явление носит Рис. 3.11 название параметрического резонанса.
При подъеме маятника совершается положительная работа (система накапливает энергию), а при опускании маятника совершается отрицательная работа (энергия системы уменьшается). Если разность энергий больше потерь энергии на трение, то маятник накапливает энергию и амплитуда его колебаний увеличивается.
Экспериментальная установка Для изучения колебаний математического маятника и явления параметрического резонанса ускорения свободного падения предназначена экспериментальная установка, общий вид которой приведен на рис.3.12.
Она включает в себя математический маятник (стальной шарик 11, висящий на нити 10). Шкала на подвижном кронштейне 9 позволяет отсчитывать углы отклонения маятника.
В пульте управления 7 смонтирован электромотор, позволяющий менять длину нити 10. На лицевой панели пульта имеется тумблер “Сеть” 5, служащий для включения электромотора; лампочка 6, сигнализирующая о включении электромотора; и ручка 8 “Частота изменения параметра”. Вращение ручки 8 по часовой стрелке увеличивает частоту изменения длины нити.
На нижнем кронштейне смонтирован фотоэлектрический датчик 12, сигнал от которого поступает на миллисекундомер 4, который служит для подсчета количества и времени колебаний маятника. На миллисекундомере имеется ряд индикаторных ламп.
Первые две показывают число полных колебаний. Остальные пять показывают число секунд, причем первые две из них показывают целое число секунд, остальные три – доли секунд. Имеются также три клавиши:
“Сеть” 1, “Стоп” 2 и “Сброс” 3, служащие, соответственно, для включения прибора, прекращения счета и повторного включения в работу.
5. Нажав на клавишу “Сброс” миллисекундомера, измерить время (t) для n = (5 – 10) полных колебаний. Остановить миллисекундомер нажатием клавиши “Стоп”.
6. Подсчитать период колебаний T t n и занести полученные значения в табл.3.2.
7. Провести не менее трех измерений и найти среднее значение периода Т.
8. Установить кронштейн со шкалой в среднее и верхнее положения и повторить измерения по п.п. 4 – 7. Результаты занести в табл.3.2
9. Построить график зависимости Т2 = f(L).
Определение логарифмического декремента затухания.
1. Поставить кронштейн со шкалой в среднее положение.
2. Отвести маятник на угол 0 = (7 – 8) и отпустить.
3. Нажать клавишу “Сброс” миллисекундомера и замерить число колебаний N, во время которых максимальный угол отклонения маятника уменьшится в два раза 0 2.
4. По формуле (3.67) рассчитать логарифмический коэффициент затухания.
Исследование параметрического резонанса.
1. Ручку 8 “Частота изменения параметра” повернуть по часовой стрелке до упора.
2. Включить тумблер 5 “Сеть” на пульте управления 7.
3. Отвести шарик на угол (5 – 7) и отпустить.
4. Медленно вращая ручку “Частота изменения параметра” добиться резонанса системы, при котором амплитуда колебаний маятника будет резко возрастать.
5. Выключить тумблер 5 “Сеть” (не изменяя положение ручки “Частота изменения параметра”).
6. Замерить частоту колебаний маятника. Для этого отвести шарик на угол (5 – 7), отпустить и, включив миллисекундомер, измерить время t для n = (5 – 10) полных колебаний. Результаты измерений занести в табл.3.3.
7. Определить частоту колебаний f n t.
8. Повторить измерения по п.п. 6, 7 не менее трех раз.
9. Определить среднее значение частоты колебаний f.
10. Определить частоту изменения параметра. Для этого, не отклоняя шарик от положения равновесия, включить тумблер 5 “Сеть”.
11. Измерить время t1 для n1 = (10 – 15) подъемов и опускания нити (если фотодатчик установки не срабатывает, то использовать механический секундомер, считая число подъемов–опусканий нити).
12. Подсчитать частоту колебаний f1 n1 t1.
13. Повторить измерения по п.п. 11, 12 не менее трех раз.
14. Определить среднее значение частоты изменения параметра f1.
15. Найти отношение средней частоты изменения параметра к средней частоте колебаний f1 f.
16. Отключить установку от сети.
1. В чем отличие параметрических колебаний от свободных и вынужденных?
2. Как изменяется энергия маятника при параметрических колебаниях и при затухающих колебаниях с вязким трением?
3. Каково должно быть соотношение между частотой изменения параметра и собственной частотой колебаний системы для того, чтобы наблюдался параметрический резонанс?
4. Какие колебания будет совершать маятник, если подводимая энергия будет равна потерям энергии в системе?
Величины Т, m, r и L могут быть найдены непосредственными измерениями.
Порядок выполнения работы
1. Отклонив колесо с добавочным грузом от положения равновесия на небольшой угол (в пределах 10 ), определить с помощью секундомера время t для n = (10 – 15) полных колебаний и вычислить период колебаний T t n. Измерения повторить не менее трех раз.
2. Измерить штангенциркулем расстояние L между осями махового колеса и цилиндра, а также диаметр цилиндра (2r). Измерения повторить несколько раз. Все измерения записать в табл.3.4.
3. Рассчитать средние арифметические значения измеряемых величин и определить по формуле (3.73) среднее значение момента инерции J 0. Масса добавочного груза указана на установке.
4. Вычислить доверительную и относительную погрешности результата.
1. От чего зависит момент инерции тела?
2. Напишите исходные уравнения для вывода расчетной формулы в данной работе и объясните физический смысл всех входящих в эти уравнения величин.
3. Каково назначение дополнительного груза в данной работе? Как определяется его момент инерции?
Экспериментальная установка Для определения моментов инерции твердых тел предназначена экспериментальная установка, общий вид которой приведен на рис.3.15.
3. Определить период крутильных колебаний по формуле T t n.
4. Для средних значений периодов колебаний рассчитать моменты инерции JА, Jх, J y и Jz по формулам (3.81) и (3.82).
5. Определить доверительную и относительную погрешность измерений для одной из величин: Jх, J y, Jz (по указанию преподавателя).
1. В чем состоит метод крутильных колебаний?
2. Что такое момент инерции?
3. В чем заключается метод крутильных колебаний для расчета моментов инерции тела?
4. Объясните различие в величинах полученных моментов инерции JА, Jх, J y и Jz.
ЛАБОРАТОРНАЯ РАБОТА № 11 Определение момента инерции тела при помощи трифилярного подвеса Цель работы: определение момента инерции тела по параметрам крутильных колебаний тела на трифилярном подвесе.
Методика измерений и экспериментальная установка Моменты инерции различных тел относительно оси, проходящей через их центр тяжести, могут быть определены методом крутильных колебаний на трифилярном подвесе.
Трифилярный подвес состоит из диска массой mд и радиусом R, подвешенного к неподвижному диску меньшего радиуса r на трех симметрично расположенных нитях длиной L (рис.3.16а). Подвес может совершать крутильные колебания относительно оси, проходящей через центр тяжести диска перпендикулярно к его плоскости.
При повороте нижнего диска относительно верхнего на небольшой ( 10 ) все нити принимают наклонное положение, и центр угол тяжести диска при этом поднимается на высоту h = h1 – h2 (рис.3.16б).
Угол отклонения от положения равновесия при гармонических крутильных колебаниях изменяется по закону
гармонических крутильных колебаний при соответствующих значениях J и m.
Для определения момента инерции исследуемого тела относительно оси, проходящей через центр тяжести, нужно построить с помощью эталонных грузов градуировочную кривую J = f(mT2).
Для этого на нижний диск подвеса нанесены концентрические окружности радиусом R1, R2. Rn. На каждой окружности сделано несколько отверстий на одинаковом расстоянии друг от друга.
Располагая эталонные грузы симметрично на том или ином расстоянии
Ri от оси вращения, мы получаем значение момента инерции:
– момент инерции каждого из грузов относительно оси вращения системы (по теореме Штейнера).
2. Помещая грузы последовательно на первую, вторую и т.д.
окружности, определить в каждом случае время t для n = (10 – 15) полных колебаний и рассчитать период колебаний T t n, где n число колебаний.
4. Определить среднее значение периода колебаний для каждой серии измерений Т.
5. Рассчитать суммарную массу системы m m д km 0, где
– масса нижнего диска, k – число грузов.
6. Определить момент инерции системы J по формуле (3.87).
7. Построить график зависимости J от ( mT 2 ). Экспериментальные точки должны располагаться около прямой.
9. Измерения по п.8 повторить не менее трех раз. Рассчитать период колебаний T t n, определить среднее значение Т и величину ( m T 2 ), где m m д m т. Результаты измерений занести в табл.3.12.
11. По построенному ранее градуировочному графику для этого значения ( mT 2 ) найти момент инерции системы J J д J т, откуда Jт J Jд.
12. Рассчитать доверительную и относительную погрешность измерений.
1. Какова цель данной работы? Опишите метод исследования.
2. Примените закон сохранения энергии к трифилярному подвесу и получите формулу для периода его гармонических крутильных колебаний.
3. Найдите зависимость между моментом инерции трифилярного подвеса и произведением его массы на квадрат периода его крутильных гармонических колебаний. Изобразите ее на графике.
4. Каково назначение цилиндрических грузов?
ЛАБОРАТОРНАЯ РАБОТА № 13 Исследование свободных колебаний пружинного маятника Цель работы: изучение зависимости периода колебаний пружинного маятника от массы тела и жесткости проволоки.
Методика измерений и экспериментальная установка В данной работе исследуются гармонические колебания пружинного маятника (рис.3.17), состоящего из
Измерив период колебаний для различных значений массы m при k = const, можно получить график зависимости квадрата периода колебаний Т2 от массы m колеблющегося тела. График функции Т2 = f(m) при k = const в соответствии с (3.88) при гармонических колебаниях должен быть прямой линией, проходящей через начало координат.
Измерив период колебаний для различных значений k при одной и той же массе m = const, можно получить график зависимости квадрата периода колебаний Т2 от 1 k. График функции T 2 f (1 k ) тоже должен быть прямой линией, проходящей через начало координат.
Экспериментальная установка состоит из подставки, к которой прикреплены пружины 1, 2, 3 разной длины, обладающие различными упругими свойствами. К пружинам прикреплены подвесы, на которые помещают цилиндрические грузы массой mгр 0,05 кг каждый (масса подвеса также 0,05 кг). Число грузов можно изменять, следовательно, можно изменять силу, растягивающую пружину, и колеблющуюся массу.
2. Добавляя постепенно грузы рассчитать по формуле (3.89) значения коэффициента возвращающей силы k1, k1. для той же пружины 1. Результаты измерений занести в табл.3.14.
3. Найти среднее арифметическое значение k1 для первой пружины.
4. Измерения по п.п 1. 3 повторяют для второй и третьей пружины.
5. Рассчитать средние значения 1 k1, 1 k 2, 1 k 3 и записать в табл.3.15.
1. Написать дифференциальное уравнение для колебания груза на пружине.
2. Как в работе определяется коэффициент возвращающей силы пружины?
3. От чего зависит период колебаний пружинного маятника?
ЛАБОРАТОРНАЯ РАБОТА № 14 Исследование крутильных колебаний Цель работы: изучение зависимости периода крутильных колебаний от момента инерции тела и упругих свойств проволоки.
Период таких колебаний выражается формулой (3.30)
Целью работы является экспериментальная проверка соотношения (3.90).
Измерив период колебаний крутильного маятника для различных значений момента инерции J при c = const, можно получить график зависимости квадрата периода колебаний Т2 от момента инерции J колеблющегося тела. График функции Т2 = f(J) в соответствии (3.90) должен быть прямой линией, проходящей через начало координат.
Измерив период колебаний для различных значений с и одного и того же тела (J = const), можно получить график зависимости T 2 f (1 c). График этой функции также должен быть прямой линией, проходящей через начало координат.
Экспериментальная установка (рис.3.21) состоит из перекладины, к которой прикреплены три проволоки разной длины L1, L2, L3, обладающие различными упругими свойствами. К проволокам прикреплены подвесы 1, 2, 3, на которые помещают одинаковые цилиндрические грузы с известным значением момента инерции. Число грузов на каждой проволоке можно изменять, следовательно, можно изменять и момент инерции колеблющейся системы. Момент инерции подвеса J п для данной установки мал и при расчетах им можно пренебречь.
Коэффициент возвращающего момента может быть определен по формуле (3.25):
Значения модуля сдвига G, радиуса проволоки r, а также момента инерции груза J и приведены в таблице на подставке установки.
Порядок выполнения работы Упражнение 1.
Проверка зависимости Т2 = f(J) при c = const.
1. Найти опытным путем периоды колебаний одного, двух, трех и т.д. грузов на подвесе на одной и той же проволоке. Для этого на подвес сначала поместить один груз с моментом инерции J, суммарный момент инерции системы будет J1 = J. Подвес с грузом осторожно повернуть в горизонтальной плоскости на небольшой угол (не допуская раскачивания груза) и отпустить. По секундомеру замерить время t, в течение которого совершается n полных крутильных колебаний.
2. Подсчитать период колебаний проволоки с одним грузом по формуле T t n.
проволоки по формуле (3.91) и найти величины.
с1 с 2 с 3 Результаты расчетов записать в табл. 3.17.
2. На первую проволоку положить груз (или несколько) и по секундомеру измерить время t, в течение которого совершается n колебаний.
3. Рассчитать период колебаний первой проволоки по формуле Т1 t n. Результаты записать в табл.3.17.
4. Измерения по п.п 2 – 3 повторить не менее трех раз при различных значениях числа колебаний n. Найти среднее значение
ЛАБОРАТОРНАЯ РАБОТА № 4
Изучение затухающих колебаний наклонного маятника Цель работы: Изучение колебаний наклонного маятника, расчет коэффициентов трения качения для различных углов наклона маятника и различных материалов.
Методика измерений Существуют различные виды трения. Трение качения без скольжения, возникающее, например, при качении цилиндра или шарика по горизонтальной или наклонной плоскостям называют сухим трением. Другим видом трения является вязкое трение при движении тела в жидкой или газообразной среде.
Затухающие колебания при наличии вязкого трения были рассмотрены в разделе 3.2. В данной работе рассматриваются затухающие колебания наклонного маятника – шарика, подвешенного на нити и катящегося по наклонной плоскости.
Причиной затухания колебаний в этом случае является наличие силы трения качения, зависящей от свойств материалов шарика и наклонной плоскости. При качении шарик и плоский образец деформируются из-за составляющей силы тяжести, прижимающей шарик к наклонной плоскости.
Если эти деформации мгновенно упруги, то силы взаимодействия между шариком и плоскостью ( F1 и F2 ) будут симметричны (рис.3.24а).
Экспериментальная установка В работе для определения коэффициента трения качения используется экспериментальная установка, общий вид которой приведен на рис.3.27.
На вертикальной стойке 5 основания 4 находится червячный редуктор. С его помощью осуществляется поворот и фиксация нижнего кронштейна 7. Редуктор приводится во вращение маховичком. Отсчет угла наклона образца производится по шкале 6. На нижнем кронштейне 7 крепятся: шкала 3 отсчета угловых амплитуд колебаний маятника, стержень 8, на который крепится верхний кронштейн 9, и фотоэлектрический датчик 10.
Шкала 3 представляет собой пластину, в которой имеется гнездо для установки сменных образцов. По шкале определяется угол отклонения маятника в пределах от нуля (положение равновесия) до
11. Зеркальный отражатель шкалы 3 служит для уменьшения погрешности параллакса1 при отсчете угла отклонения маятника.
Образцы представляют собой прямоугольные пластинки из различных материалов, рабочие поверхности пластинок разной чистоты обработки. Кронштейн 9 содержит механизм подвеса для регулировки длины маятника.
Маятник 11 представляет собой металлический шарик, подвешенный на тонкой нити. К шарику прикреплен острый конус для пересечения оптической оси фотоэлектрического датчика 10.
Фотоэлектрический датчик 10 размещается на нижнем кронштейне и подает электрические сигналы на миллисекундомер 2, который является прибором с цифровой индикацией времени и числа полных периодов колебаний маятника.
13. Для обоих образцов построить графики зависимости коэффициента трения качения от угла наклона плоскости к горизонту k = f( ).
14. Выключить миллисекундомер из сети.
15. Рассчитать погрешность измерений k для одного из углов наклона.
1. Какие виды трения вы знаете?
2. Какова физическая природа силы трения качения?
3. Что такое коэффициент трения качения?
4. Почему значения угловой амплитуды надо брать малыми?
5. Как и почему сила трения качения зависит от радиуса шарика R?
6. Зависит ли сила трения качения от величины поверхности соприкосновения?
7. Имеет ли размерность коэффициент трения качения?
ЛАБОРАТОРНАЯ РАБОТА № 19 Определение скорости звука в воздухе методом интерференции Цель работы: определение скорости звука в воздухе и изучение явления интерференции волн.
Методика измерений и экспериментальная установка Установка для измерения скорости звука интерференционным методом состоит из двух коленчатых трубок (рис.3.28), одно колено АВD имеет постоянную длину; длину другого колена АСD можно изменять приподнимая или опуская подвижную часть 2.
Рис. 3.28 Звук частоты f, создаваемый в телефоне 5 генератором звуковых колебаний, направляется в трубку D, где он разделяется на две звуковые волны в направлении пути АВD и АСD. В трубке A волны интерферируют, так как здесь складываются две когерентные волны.
Разность фаз этих волн определяется разностью путей в коленах установки. Трубка А соединена со слуховой трубкой 1. Удлинение колена АСD определяется по шкале 3.
Из соотношения (3.49) следует, что для определения скорости звука необходимо знать длину звуковой волны и частоту f. В данном методе длину звуковой волны можно определить путем измерения разности хода волн, соответствующей максимальному ослаблению звука вследствие интерференции. Два соседних минимума при интерференции соответствуют изменению разности хода волн на (см.
формулу 3.56).
Разность хода волн в двух трубках равна удвоенному удлинению колена АСD, поэтому положения указателя 4, соответствующие двум соседним минимумам звука, отстоят друг от друга на. Частота f L
Порядок выполнения работы
1. Подключить трубку телефона 5 к генератору звуковых колебаний 6 и разместить ее в соответствующем гнезде прибора (рис.3.28).
Установить перед началом опыта одинаковые длины трубок прибора.
2. Включить генератор тумблером “Сеть” и дать ему прогреться в течение 1. 2 мин. Установить на генераторе звуковых колебаний частоту f = 1500 Гц.
3. Услышав звук в слуховой трубке 1, медленно перемещать подвижное колено 2 прибора. Определить показания L по шкале 3, соответствующие положению указателя 4 при всех последовательных минимумах звука. Результаты измерений записать в табл.3.20.
4. Рассчитать расстояния L между всеми последовательными положениями указателя 4:
5. Определить среднее значение L для данной частоты колебаний.
7. Измерить температуру Т в помещении лаборатории.
8. Определить для каждого значения частоты колебаний скорость звука по формуле (3.107).
9. Рассчитать доверительную и относительную погрешность измерения.
1. В чем заключается условия минимума и максимума звука при интерференции двух волн?
2. Для чего в работе необходимо перемещать колено прибора?
3. В чем заключается метод определения скорости звука на основе явления интерференции?
136 Вопросы по разделу 3
1. Какое движение называется гармоническим колебанием? Каковы характеризующие его уравнения?
2. Что такое коэффициент возвращающей силы и коэффициент возвращающего момента силы? Каков физический смысл этих коэффициентов?
3. Покажите, что при гармонических колебаниях полная энергия системы сохраняется постоянной.
4. Что называется физическим и математическим маятником? Чему равны периоды их колебаний?
5. Получите дифференциальное уравнение колебаний физического маятника.
6. Получите дифференциальное уравнение гармонических крутильных колебаний.
7. Какими уравнениями характеризуются затухающие колебания?
8. Что такое коэффициент затухания и от чего он зависит?
9. Что называется логарифмическим декрементом затухания?
10. Каков физический смысл коэффициента затухания и логарифмического декремента затухания?
11. Какими уравнениями характеризуются вынужденные колебания?
12. Какова частота установивших вынужденных колебаний?
13. Что такое резонанс и когда он возникает?
14. От чего зависит резонансная частота механических колебаний?
15. Что называется упругой волной? От чего зависит скорость продольных и поперечных упругих волн?
16. Напишите уравнение плоской гармонической волны, используя понятия фазовой скорости, длины волны и волнового вектора.
17. Какие источники волн и волны называются когерентными?
18. Чему равна разность хода волн при интерференции в точках, где происходит усиление волн?
19. Чему равна разность хода волн при интерференции в точках, где происходит ослабление волн?
РАЗДЕЛ 4
Основы термодинамики. Теплоемкость вещества
4.1 Идеальный газ. Первое начало термодинамики Термодинамические системы состоят из большого числа частиц.
Термодинамический метод исследования основан на описании состояния системы с помощью некоторых макроскопических параметров, характеризующих состояние системы в целом К ним относятся объем V, давление Р и температура Т.




















Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.



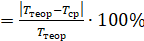
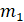 =0,033
=0,033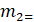 0,048
0,048