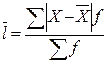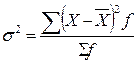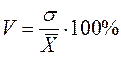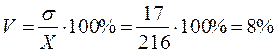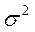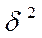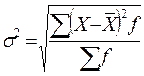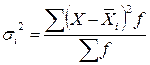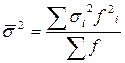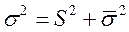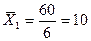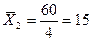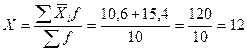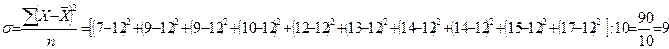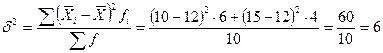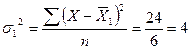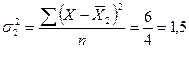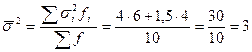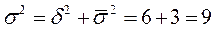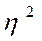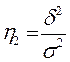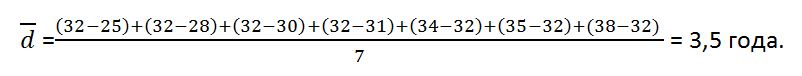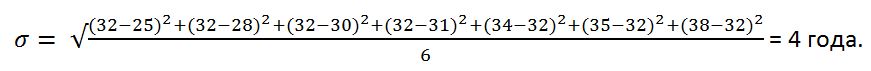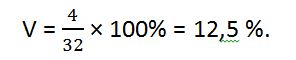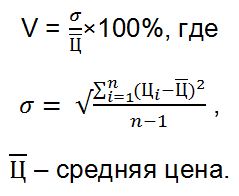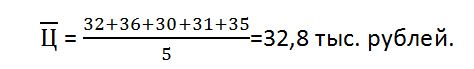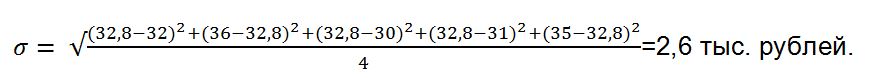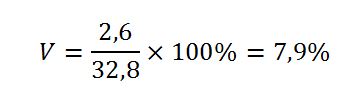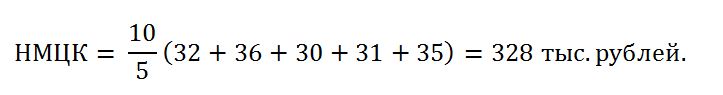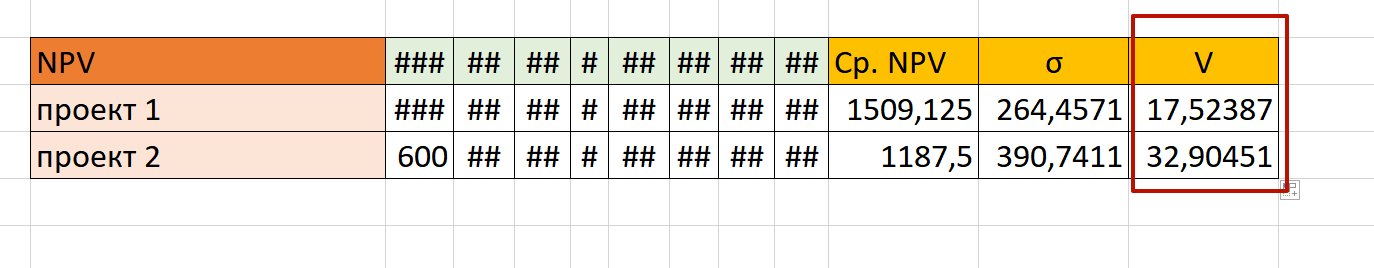Коэффициент вариации используют для оценки чего в химии

Показатели вариации

Вариация – это различие в значениях какого – либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Например работники СХПК различаются по доходам, затратам времени на работу, росту, весу, образованию, профессии и т.д.

Размах вариации R –разность между максимальным и минимальным значениями признака

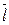
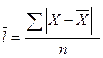
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариант в ряду. Для более точного анализа вариации необходимы показатели, которые отражают все колебания варьирующего признака и дают обобщенную характеристику. Простейший из показателей такого типа – среднее линейное отклонение .Оно определяется как среднее арифметическое из отклонений индивидуальных значений от средней без учета знака этих отклонений.

или

Среднее линейное отклонение как меру вариации признака применяют в статистической практике в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл (например, анализ состава работающих, ритмичность производства, оборот внешней торговли).

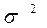
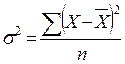
Дисперсия в зависимости от исходных данных вычисляется по формулам простой и взвешенной.

или

Дисперсия представляет собой средний квадрат отклонений вариантов от их средней величины.

Среднее квадратическое отклонение 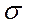равно корню квадратному из дисперсии. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем качественно однороднее совокупность и тем более типичной будет средняя величина.

Для сравнения вариаций различных признаков, а также колеблемости одного и того же признака в нескольких совокупностях используют относительный показатель вариации – коэффициент вариации V.

Коэффициент вариации характеризует, на сколько процентов в среднем отклоняются индивидуальные показатели от их среднего значения.

Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

Например, имеются данные о сменной выработке рабочих бригады, которые представлены интервальным рядов распределения:

Группы рабочих по сменной выработке изделий, шт.	Число рабо- чих f	Середина интервала x	Расчетные значения
X f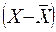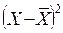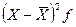
170-190	-36
190-210	-16
210-230
230-250
Итого	X	X	X

Исчислим среднюю выработку на одного работника:

(шт.)

(шт.)

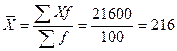
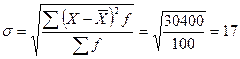
Таким образом, индивидуальные выработки рабочих за смену колеблются вокруг средней выработки в среднем на 216 изделий или 8%. Данная бригада рабочих по выработке достаточно однородна, поскольку вариация признака составляет лишь 8%, что меньше 33%.

Вариация признака обусловлена различными факторами. Определить их влияние на колеблемость индивидуальных значений признака можно при помощи трех видов дисперсий:

1) общей дисперсии

2) межгрупповой дисперсии

3) средней из внутригрупповых дисперсий

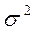
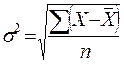
Общая дисперсия измеряет вариацию признакапо всейсовокупности под влиянием всех факторов, обусловивших эту вариацию. Она может быть вычислена по простой или взвешенной формуле:

или

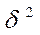
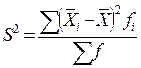
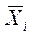
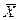
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, обусловленную влиянием факторного признака, положенного в основу группировки.

,т.е. она равна среднему квадрату отклонений групповых средних от общей средней по всей совокупности .

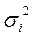
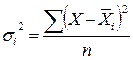
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от группировочного признака. Она исчисляется внутри каждой группы:

или

На основании внутригрупповых дисперсий вычисляют среднюю из внутригрупповых дисперсий:

Согласно правилу сложения дисперсий общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий, т.е.

Например, при изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда в цехе были получены данные, представленные в таблице:

NN п/п	Рабочие 4-го разряда	N п/п	Рабочие 5-го разряда
Выработка, шт.	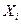		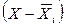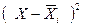Выработка, шт.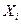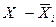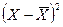
-3	-1
-1	-1
-1
-2
Итог	X	X

Результативный признак – выработка рабочего – варьирует под влиянием факторного признака (квалификации), а также под влиянием других неучтенных случайных факторных признаков. Задача заключается в измерении этих вариаций с помощью дисперсий: общей, межгрупповой и внутригрупповых.

1. Для расчета групповых дисперсий исчислим средние выработки по каждой группе и общую среднюю выработку, шт.:

по первой группе

по второй группе

в целом по десяти рабочим

Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию выработки изделий в среднем рабочими цеха.

3. Исчислим межгрупповую дисперсию

Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификационному разряду.

4. Данные для расчета внутригрупповых дисперсий представлены в таблице.

— по первой группе

— по второй группе

Средняя из внутригрупповых дисперсий:

отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих.

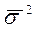
5. Проверим правило сложения дисперсий:

Очевидно, чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного признака (квалификационного разряда) на результативный признак (количество изделий на рабочего).

Для определения этой доли используется эмпирический коэффициент детерминации

показывает долю вариации результативного признака под влиянием факторного признака.

или 66,6%

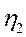
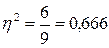
ТЕМА: «ВЫБОРОЧНЫЙ МЕТОД»

Выборочное наблюдение представляет собой такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, далее отобранная часть изучается, а затем результаты распространяются на всю исходную совокупность. Наблюдение осуществляется таким образом, что эта часть отобранных единиц представляет всю совокупность с достаточной для практике степенью точности.

Совокупность, из которой производится отбор, называется генеральной,и все ее обобщающие показатели – генеральными.

Выборочная совокупность –это совокупность единиц, отобранных из генеральной совокупности. Все ее обобщающие показатели называются выборочными.

Основными причинами, по которым во многих случаях выборочному наблюдению отдается предпочтение перед сплошным, являются:

Преимущество выборочного наблюдения по сравнению со сплошным можно реализовать, если оно организовано и приведено в соответствии с научными принципами теории выборочного метода. Это обеспечение случайности, т. е. равной возможности попадания в выборку единиц генеральной совокупности, и достаточного числа единиц отбора.

Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (т.е. средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических исследованиях (сплошных и выборочных) возникают ошибки.

Ошибки регистрации могут возникать и при сплошных, и при выборочных наблюдениях. Они могут иметь случайный (непреднамеренный) и систематический (преднамеренный) характер.

Ошибки репрезентативности (представительности) присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенной с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборочных и генеральных характеристик.

Ошибки репрезентативности возникают вследствие двух причин:

1) из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки)

2) в результате самого отбора (случайные ошибки)

Систематические ошибки выборки устраняются. Случайные ошибки устранить нельзя, но их рассчитывают и учитывают при переносе выборочных характеристик на генеральную совокупность.

Средняя ошибка выборки представляет собой такое расхождение между средними выборочной и генеральной совокупностей, которое не превышает среднеквадратическое отклонение в выборке.

Предельной ошибкой называется максимальное расхождение средних характеристик выборочной и генеральной совокупностей при заданной вероятности появления этой ошибки.

По методу отбора различают повторную и бесповторную выборки.

При повторной выборке ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами вновь попасть в выборку.

При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует.

По степени охвата единиц совокупности различают большие и малые (n

Источник

Что такое коэффициент вариации и для чего он нужен

Коэффициент вариации – это статистический показатель, какой широко используется в финансовых расчетах. Он показывает степень разброса значений в числовой последовательности. А именно, насколько любая из величин отклоняется от средней. Если вариация слишком высока, то оценивать среднее значение некорректно. В этой ситуации обыкновенно исключают минимальное и максимальное число.

Показатель чаще всего применяется при формировании начальной минимальной цены контракта по 44-ФЗ. Она должна опираться на выборке рыночных цен, а в их оценке как раз и используется вариация. Кроме того, применяется при анализе рисков инвестиционных проектов и доходности ценных бумаг. В цельном, показатели вариации применимы в любой сфере, где требуется оценить совокупность данных и их разнообразие: статистика, математика, экономический разбор, социология, маркетинг и т.д.

Формулы расчета в статистике

Для оценки совокупности значений и их однородности применяют следующие инструменты:

Рассмотрим применение указанных формул на примере оценки среднего возраста трудящихся в отделе кадров. В указанном подразделении трудятся 7 сотрудников, которым 25, 28, 30, 31, 34, 35 и 38 лет. Размах вариации покажет нам разницу в году между самым младшим и самым старшим из них:

Рассчитаем среднее линейное отклонение. Для этого для начала найдем посредственный возраст в отделе: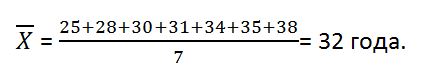Теперь посчитаем среднее линейное отклонение:

Соответственно, мы можем сказать, что средний возраст сотрудников составляет 32 ± 3,5 года.

Среднеквадратичное отклонение покажет то же самое, но немало точно:

Коэффициент вариации покажет, на сколько процентов возраст каждого работника отличается от среднего по отделу:

Оценка коэффициента вариации

Если со посредственными значениями и отклонениями от них все понятно, то зачем же рассчитывается коэффициент вариации? С его помощью можно судить, насколько показательно усредненное смысл и можно ли по нему судить о выборке в целом. В нашем примере он позволит ответить на вопрос, можно ли утверждать то, что посредственный возраст по отделу кадров составляет 32 года. Либо реальные показатели будут слишком сильно выделяться от полученного значения?

В статистике определены следующие критерии оценки:

Если показатель вариации превышает 33%, то выборка почитается неоднородной и судить о ней по средним значениям никак нельзя. При незначительном разбросе достоверность средних будет максимальной. В нашем образце вариативность средняя и в целом оценивать возраст по средним значениям с учетом отклонений вполне можно.

Если посмотреть на числовой ряд, то видать, что только 2 сотрудника существенно отклоняются от среднего возраста. На практике при слишком высокой вариативности из анализа исключают максимальное и минимальное смыслы, после чего проводят повторную проверку. Также часто по коэффициенту вариации сравнивают разные выборки. В нашем образце это слабо применимо, но, например, при анализе цен конкурентов будет вполне эффективно для выбора наиболее подходящей для анализа совокупности смыслов.

Читайте также! Выплата дивидендов учредителям ООО и АО в 2019 году

Применение при закупках по 44-ФЗ

Федеральный закон 44-ФЗ регулирует распорядок проведения государственных закупок. Его цель – не допустить злоупотреблений должностных лиц и передачу контрактов «своим» фирмам по завышенным/заниженным стоимостям. Именно для этого в законе определен порядок того, как устанавливается начальная минимальная цена контракта (НМЦК) – та, с какой и будут начинаться торги.

Методика определения начальной минимальной цены

Законом предусмотрено 5 методов определения НМЦК:

При этом наиболее предпочтительным и рекомендуемым является именно первоначальный. Его суть в том, что анализируются цены точно таких же товаров или услуг (идентичных) либо при их отсутствии схожих (однородных). Оба понятия четко установлены:

Данный порядок определен статьей 22 вышеуказанного закона. В 2019 году в нее было привнесено несколько изменений:

Как рассчитать НМЦК

Для расчета начальной цены заказчику необходимо составить выборку рыночных цен. Это можно сделать вытекающими способами:

Обычно используется первый способ. Нескольким поставщикам отправляются запросы введённой формы, а на основании полученных ответов и осуществляются расчеты по следующей формуле:

Коэффициент вариации в данном случае предзнаменований вид:

Пример расчета

Рассмотрим, как рассчитать НМЦК и коэффициент вариации на примере закупки 10 холодильников для больницы. От 5 поставщиков бывальщины получены коммерческие предложения со следующими ценами: 32, 36, 30, 31 и 35 тыс. рублей за штуку.

Оценим однородность ценовых предложений линией расчета коэффициента вариации. Для начала рассчитаем среднюю цену:

Теперь необходимо найти среднеквадратичное отклонение:

И, наконец, рассчитываем коэффициент вариации:

V меньше 10%, таким манером, делаем вывод о том, что выборка однородна и ее можно использовать для установки закупочных цен для торгов.

Посчитаем минимальную цену контракта:

Использование в оценке рисков

В финансовом разборе степень отклонения показателя от среднего значения показывает уровень риска. Например, если прибыль в разные годы существования компании то существенно всходит, то падает в убыток, инвестировать в нее опасно. То же самое касается ценных бумаг и любых других биржевых инструментов. Самыми привлекательными будут стабильные бумаги с минимальными колебаниями котировок при неплохом росте. Таким образом, есть еще два направления, где активно используется коэффициент вариации: оценка рисков проекта и рисков по доходности ценных бумаг.

Декламируйте также! Организация и внедрение бережливого производства на предприятии

Инвестиционные проекты

Как правило, при оценке рисков инвестиционных проектов используются:

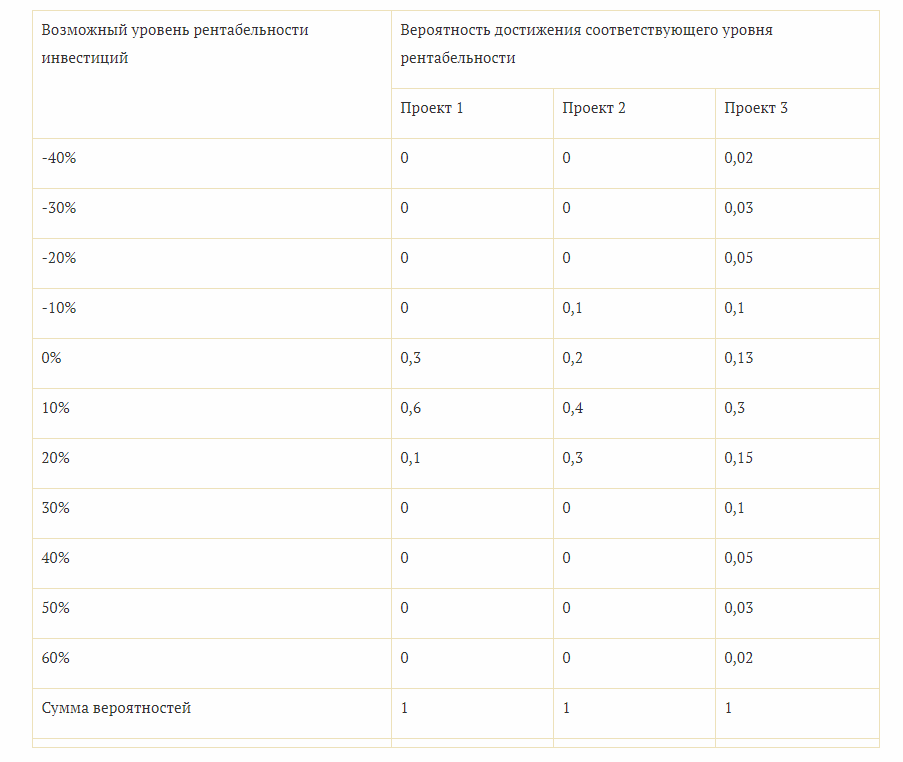
Обычно сравниваются несколько проектов по всем критериям. Также есть вариант рассмотреть возможность достижения того или другого уровня рентабельности:

В данном случае все проекты будут рискованными, поскольку коэффициент вариации составит 65%, 95% и 198% соответственно. Но риск по первому немало чем в 2 раза ниже, чем по третьему, поэтому из представленных вариантов лучше выбрать его.

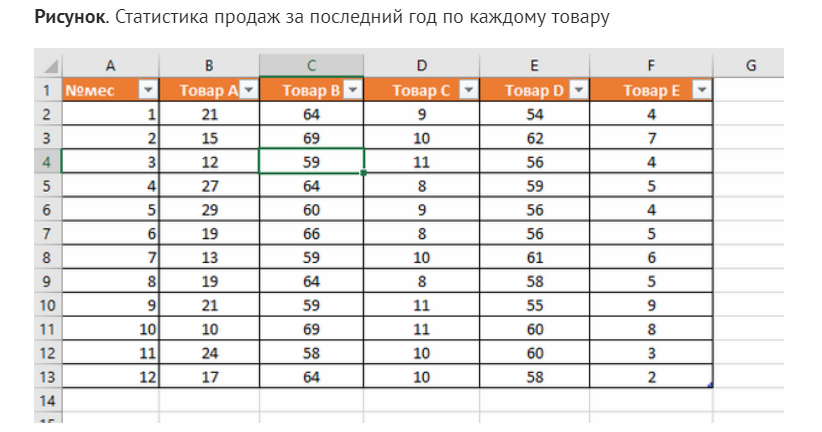
Нередко используют коэффициент при анализе спроса и принятии решении о закупках. Так, анализируется статистика продаж товара, после чего определяется, что закупать в первую очередь, а что только при наличии предзаказа:

В этом примере коэффициенты вариации по товарам А, B, C, D и E будут равны 30%, 6%, 12%, 4%, 38% соответственно. Очевидно, что спрос на продукцию E нестабилен и мощно колеблется в разные месяцы, поэтому заказывать целую партию рискованно.

Ценные бумаги

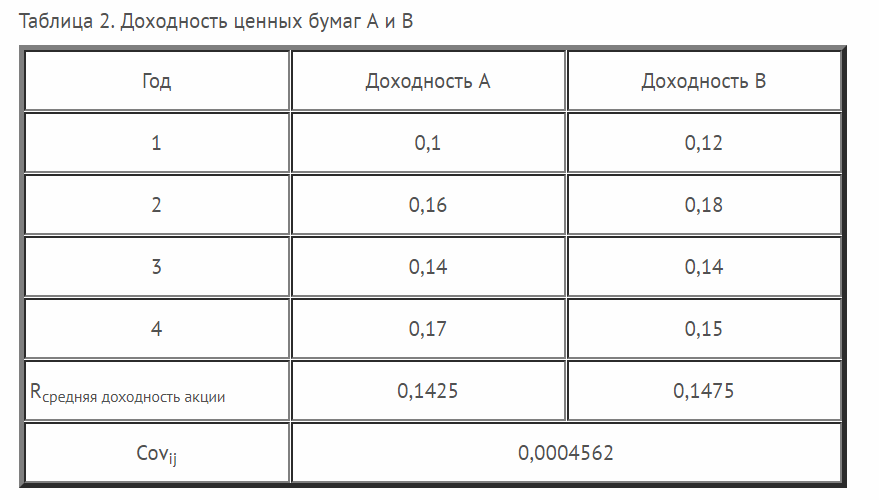
Что касается торговли на бирже, то тут можно оценивать в двух вариантах:

В первом случае, имея эти о колебаниях котировок в прошлом, мы сможем оценить риск вложения именно в данный инструмент. Во втором варианте можно оценить риск портфеля инвестиций на основании совокупности доходности любой его составляющей. Также риск портфеля можно проанализировать на основании совокупности вариаций каждой его составляющей во временном интервале. Все эти методики используются в комплексном анализе рисков инвестиционного портфеля.

Расчет в MS Excel

Как при расчете цены контракта, так и при оценке инвестиционных проектов выполнять громоздкие вычисления квадратичного отклонения и коэффициента вариации вручную весьма трудоемко. Поэтому рассмотрим, как быстро и просто выполнить это при помощи электронной таблицы Excel.

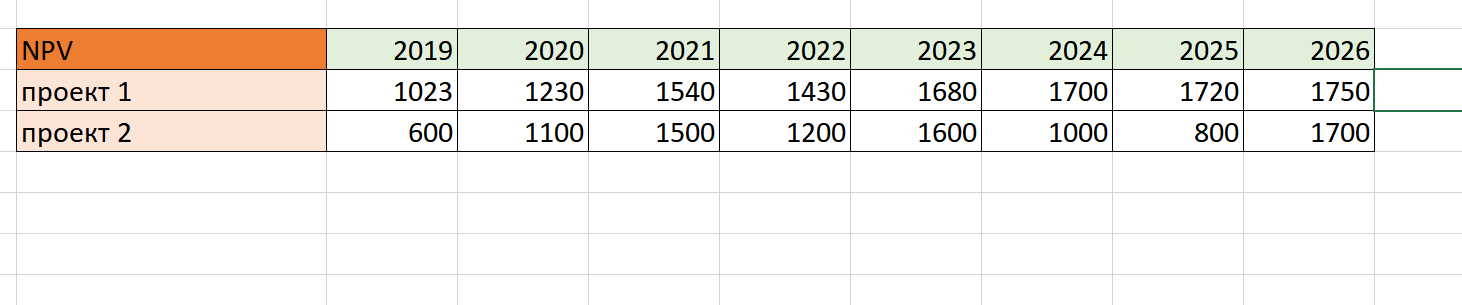
Для начала открываем редактор и создаем таблицу с отправными данными. Для примера возьмем два инвестиционных проекта с показателями NPV за 8 лет.

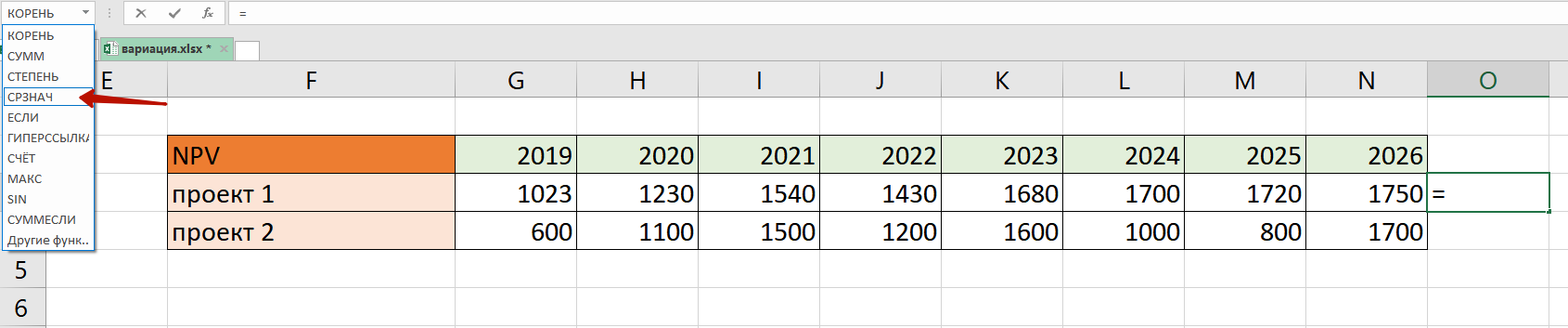
Далее находим среднее значение прибыли при помощи функции СРЗНАЧ:

Вышли вот такие значения:

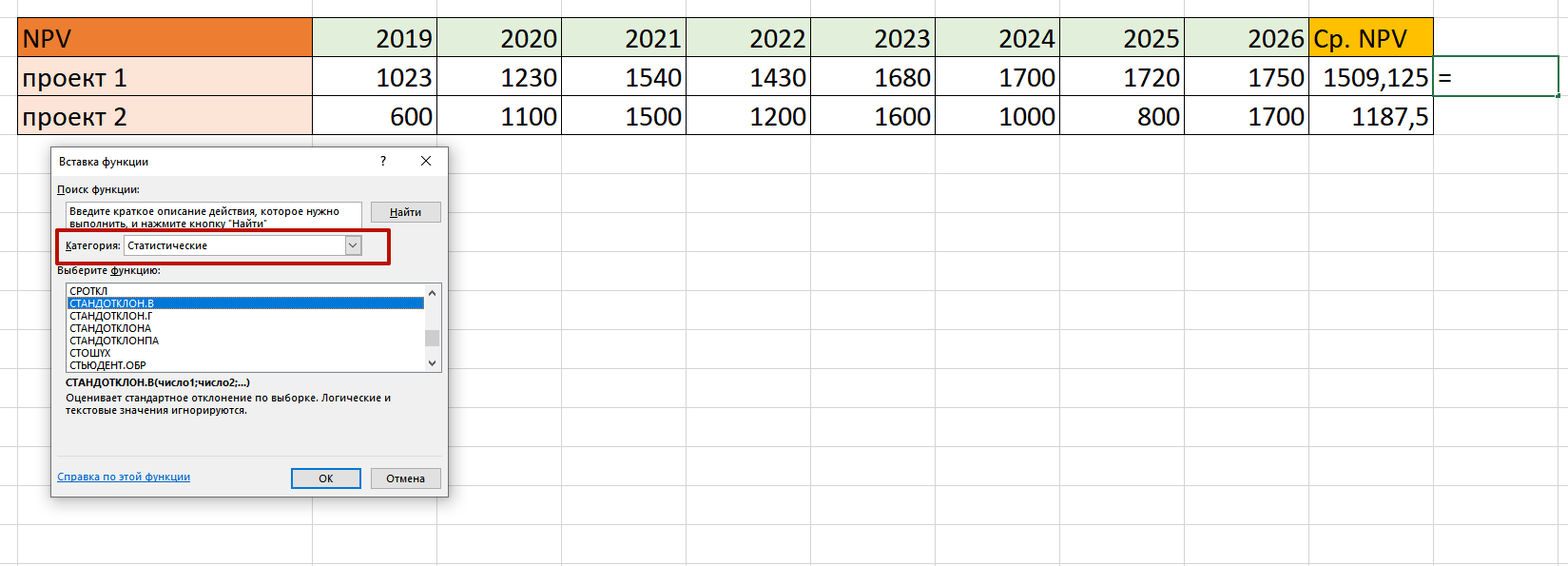
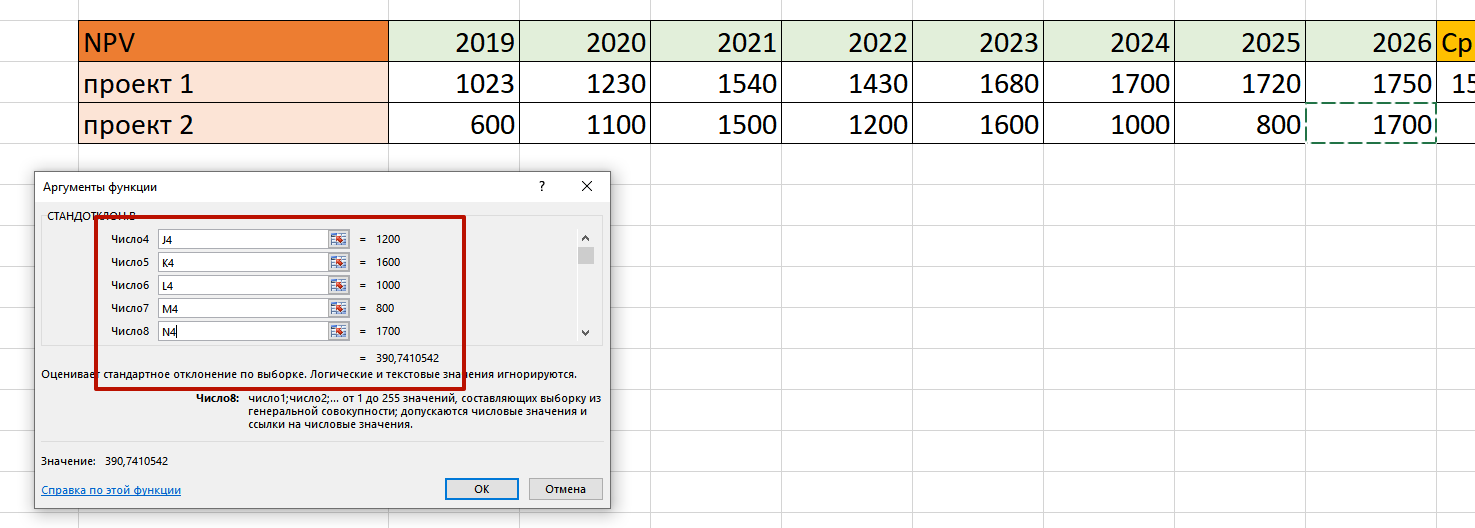
Теперь необходимо вычислить среднеквадратичное отклонение. Для этого предназначена функция СТАНДОТКЛОН.В

Обратите внимание, что в любую строку необходимо вбить одну ячейку, а не выбирать весь диапазон:

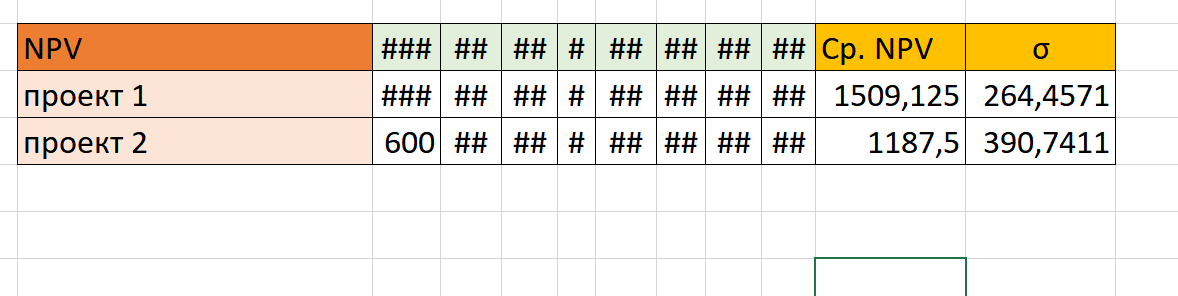
Таким образом, у нас есть рассчитанные посредственные значения доходности и среднеквадратичного отклонения по двум проектам:

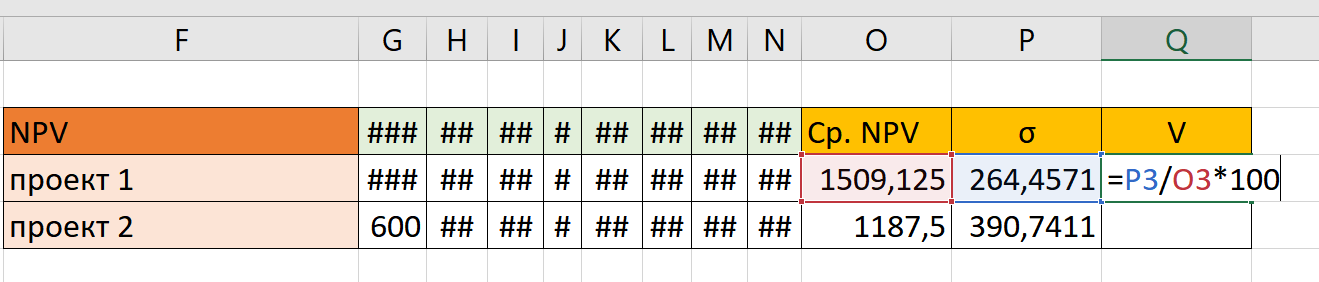
Теперь нам нужно найти коэффициент вариации. Для этого мы попросту вписываем вручную формулу: ячейку σ делим на среднюю доходность и умножаем на 100:

Таким образом, получаем следующие смыслы коэффициента вариации:

Можно сделать вывод о том, что первый проект менее рисковый, чем второй.

Источник