граф с какими свойствами называют деревом что такое корень дерева ветви листья
Какой граф называется деревом? Что такое дерево в информатике?
Содержание:
Граф-дерево является очень распространенным видом графов в информатике. Они нужны для хранения какой-либо информации в нелинейной структуре в иерархическом порядке.
Граф — это структура, состоящая из множества вершин, соединенных ребрами. Все в своей жизни видели транспортные схемы (передвижение автобусов или метро). Если эти схемы смоделировать в компьютере, то остановки и станции — это будут вершины графа, а маршрут транспорта между остановками/станциями — ребра графа.
В зависимости от того, каким образом расположены вершины, какое отношение между ними и каким способом они соединяются между собой ребрами, различают различные виды графов. Граф-дерево — это всего лишь один из множества видов графов.
Граф-дерево
Самое главное, все имена вы соединяли линиями зависимости между собой. Например, свое имя соединили с именами братьев и сестер и с именами своих родителей. Имена ваших родителей вы соединили с именами их братьев и сестер и с их родителями и т. д.
В информатике, граф-дерево выглядит точно так же, как и ваше генеалогическое дерево, только вместо имен — вершины, а вместо линий, связывающих имена — ребра.
Охарактеризовать граф-дерево в информатике можно так — это связный граф, где между двумя вершинам есть единственный связный путь. Вернемся к нашему дереву. Ваше имя будет связано линиями только с вашими родителями и вашими братьями/сестрами, с другими именами дерева у вас нет прямой связи. Например, с вашими дядями, тетями, бабушками и дедушками вы будете связаны только через ваших родителей, а не напрямую. А с вашей прабабушкой или вашим прадедушкой вы будете связаны только через родителей и бабушек с дедушками.
То есть граф-дерево в информатике следует строгой иерархии — одни элементы находятся «наверху» графа и будут называться «корнем дерева», другие элементы будут чуть ниже и будут называться «потомками», от «потомков» будут исходить «листья» — это те вершины, которые не имеют «потомков». Любой элемент верхнего уровня по отношению к нижнему уровню будет называться «предком».
Вернемся к нашему генеалогическому дереву. Бабушка с дедушкой (или прабабушка с прадедушкой, то есть в зависимости до какой глубины своих предков вы дойдете) будут корнем вашего граф-дерева (либо подкорнем, если у вас в корне будут прабабушка с прадедушкой). Ваши родители — это «потомки» вашего граф-дерева и бабушка с дедушкой для них будут «предками» вашего дерева. Вы будете «листьями» граф-дерева, потому что у вас пока нет своего потомства, как только у вас появятся дети, то вы станете «потомками» графа, а ваши дети «листьями». Ваши родители для вас будут «предками» графа.
Все что нужно знать о древовидных структурах данных
Jul 1, 2018 · 14 min read
Деревья прекрасны. Вот рисунок, который я сделал ребенком
Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».
В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.
Однако в самом начале и зучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.
Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.
Из этой статьи вы узнаете:
Давайте начнем наше учебное путешествие 🙂
Определения
Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.
Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.
Давайте вплотную займемся реальными примерами
Что я имею в виду, когда я говорю иерархически?
Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.
Мое фамильное дерево
Приведенный рисунок — это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми — мои дедушки и бабушки.
Тошиаки и Джулиана — мои родители.
ТК, Юдзи, Бруно и Кайо — дети моих родителей (я и мои братья).
Структура организации — еще один пример иерархии.
Структура компании является примером иерархии
В HTML, объектная модель документа (DOM) представляется в виде дерева.
Объектная модель документа (DOM)
Техническое определение
Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.
Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.
Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.
Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.
Другими важными понятиями являются высота и глубина.
Высота дерева — это длина самого длинного пути к листу.
Глубина узла — это длина пути к его корню.
Справочник терминов
Бинарные деревья
Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.
“В информатике бинарным (двоичным) деревом называется иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.” — Wikipedia
Рассмотрим пример бинарного дерева.
Давайте закодируем бинарное дерево
Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?
Вот наш двоичный класс дерева.
Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.
Давайте это проверим:
Перейдем к части вставки. Что нам нужно здесь сделать?
Мы реализуем метод вставки нового узла справа и слева.
Давайте это нарисуем 🙂
Вот программный код:
Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.
И мы делаем то же самое, чтобы вставить правый дочерний узел.
Но не полностью. Осталось протестировать.
Давайте построим следующее дерево:
Подытоживая изображенное дерево, заметим:
Таким образом, вот код для нашего дерева следующий:
Теперь нам нужно подумать об обходе дерева.
У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).
• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.
• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.
Давайте подробно рассмотрим каждый из алгоритмов обхода.
Поиск в глубину (DFS)
DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.
Результатом этого алгоритма будет: 1–2–3–4–5–6–7.
Давайте разъясним это подробно.
Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.
После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).
Предварительный обход
Именно это мы и делали в вышеприведенном примере.
1. Записать значение узла.
2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.
3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.
Дерево (теория графов)
Лес — упорядоченное множество упорядоченных деревьев.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.
Связанные понятия
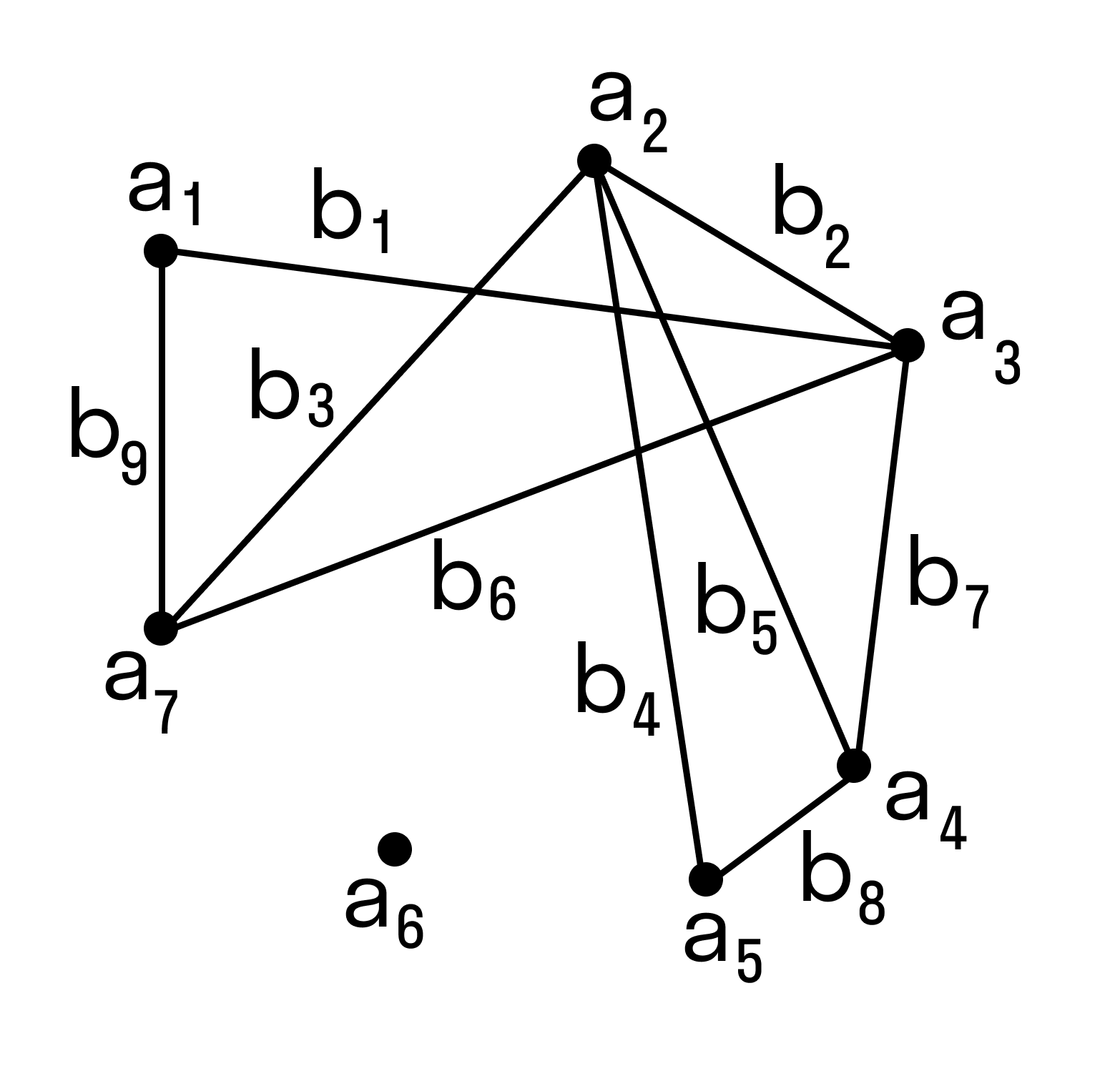
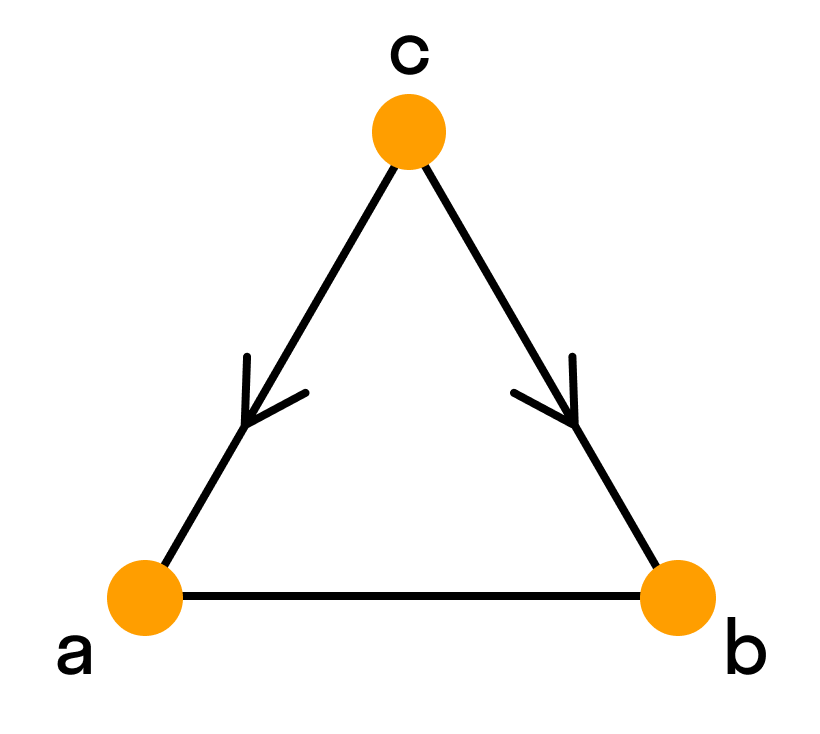
В теории графов вершиной называется фундаментальная единица, образующая графы — неориентированный граф состоит из множества вершин и множества рёбер (неупорядоченных пар вершин), в то время как ориентированный граф состоит из множества вершин и множества дуг (упорядоченных пар вершин). На рисунках, представляющих граф, вершина обычно обозначается кружком с меткой, ребро — линией, дуга — стрелкой, соединяющей вершины.
Упоминания в литературе
Связанные понятия (продолжение)
Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).
Кликой неориентированного графа называется подмножество его вершин, любые две из которых соединены ребром. Клики являются одной из основных концепций теории графов и используются во многих других математических задачах и построениях с графами. Клики изучаются также в информатике — задача определения, существует ли клика данного размера в графе (Задача о клике) является NP-полной. Несмотря на эту трудность, изучаются многие алгоритмы для поиска клик.
В теории графов графом-циклом называется граф, состоящий из единственного цикла, или, другими словами, некоторого числа вершин, соединённых замкнутой цепью. Граф-цикл с n вершинами обозначают как Cn. Число вершин в Cn равно числу рёбер и каждая вершина имеет степень 2, то есть любая вершина инцидентна ровно двум рёбрам.
Орграф называется сильно связным (англ. strongly connected), если любые две его вершины сильно связны. Две вершины s и t любого графа сильно связны, если существует ориентированный путь из s в t и ориентированный путь из t в s.
В теории графов outerplanar graph — это граф, допускающий планарную диаграмму, в которой все вершины принадлежат внешней грани.
В теории графов рёберным графом L(G) неориентированного графа G называется граф L(G), представляющий соседство рёбер графа G.
В теории графов мультиграфом (или псевдографом) называется граф, в котором разрешается присутствие кратных рёбер (их также называют «параллельными»), то есть рёбер, имеющих те же самые конечные вершины. Таким образом, две вершины могут быть соединены более чем одним ребром (тем самым мультиграфы отличаются от гиперграфов, в которых каждое ребро может соединять любое число вершин, а не в точности две).
В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества.
В теории графов графом пересечений называется граф, представляющий схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.
В теории графов неориентированный граф H называется минором графа G, если H может быть образован из G удалением рёбер и вершин и стягиванием рёбер.
В теории графов совершенным графом называется граф, в котором хроматическое число любого порождённого подграфа равно размеру максимальной клики этого подграфа. Благодаря строгой теореме о совершенных графах, с 2002 года известно, что совершенные графы — это то же самое, что и графы Бержа. Граф G является графом Бержа если ни G, ни его дополнение не имеет порождённых циклов нечётной длины (5 и более рёбер).
Граф решётки — это граф, рисунок которого, вложенный в некоторое евклидово пространство Rn, образует регулярную мозаику. Это подразумевает, что группа биективных преобразований, переводящая граф в себя, является решёткой в теоретико-групповом смысле.
Теория графов. Основные понятия и виды графов
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
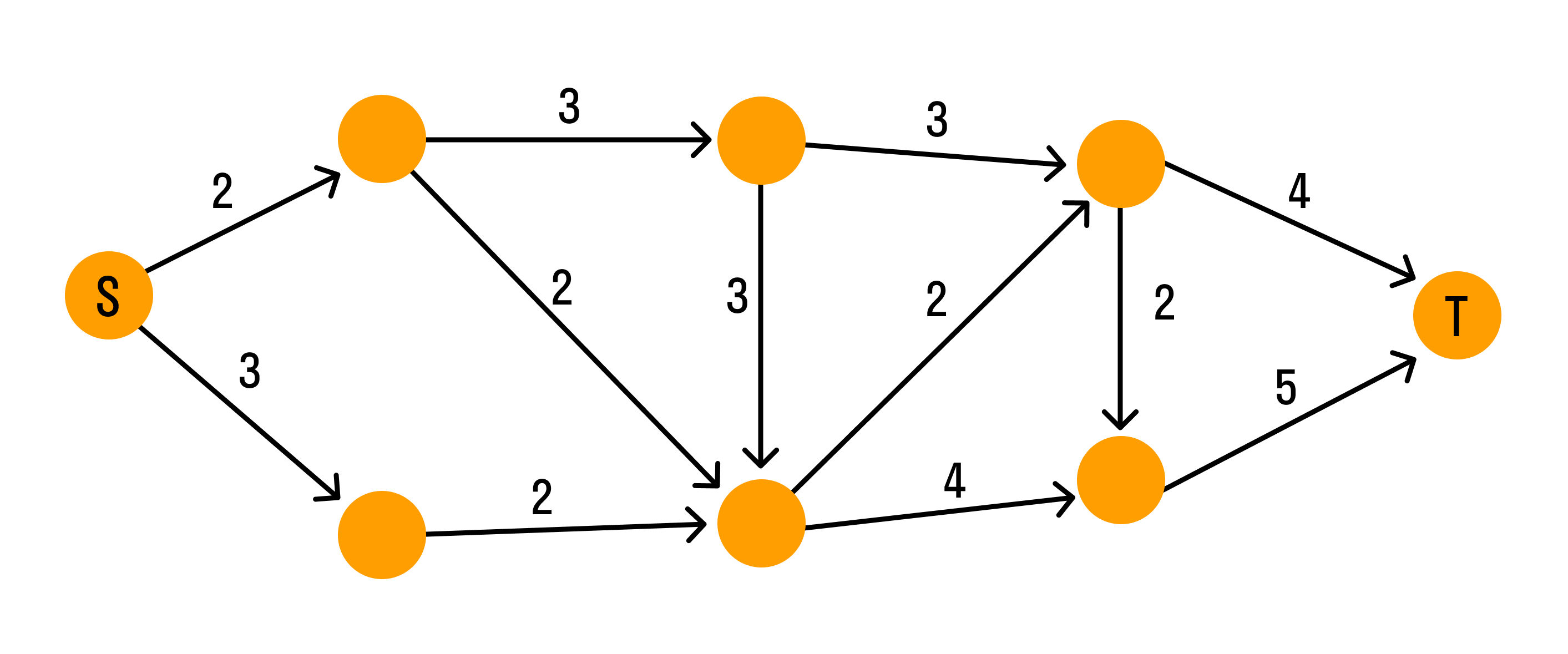
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
Лемма о рукопожатиях
В любом графе сумма степеней всех вершин равна удвоенному числу ребер.
Доказательство леммы о рукопожатиях
Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.
Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).
Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.
Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.
Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.
Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.
Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.
Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.
Путь и цепь в графе
Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Циклом называют путь, в котором первая и последняя вершины совпадают.
Путь или цикл называют простым, если ребра в нем не повторяются.
Если в графе любые две вершины соединены путем, то такой граф называется связным.
Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.
Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.
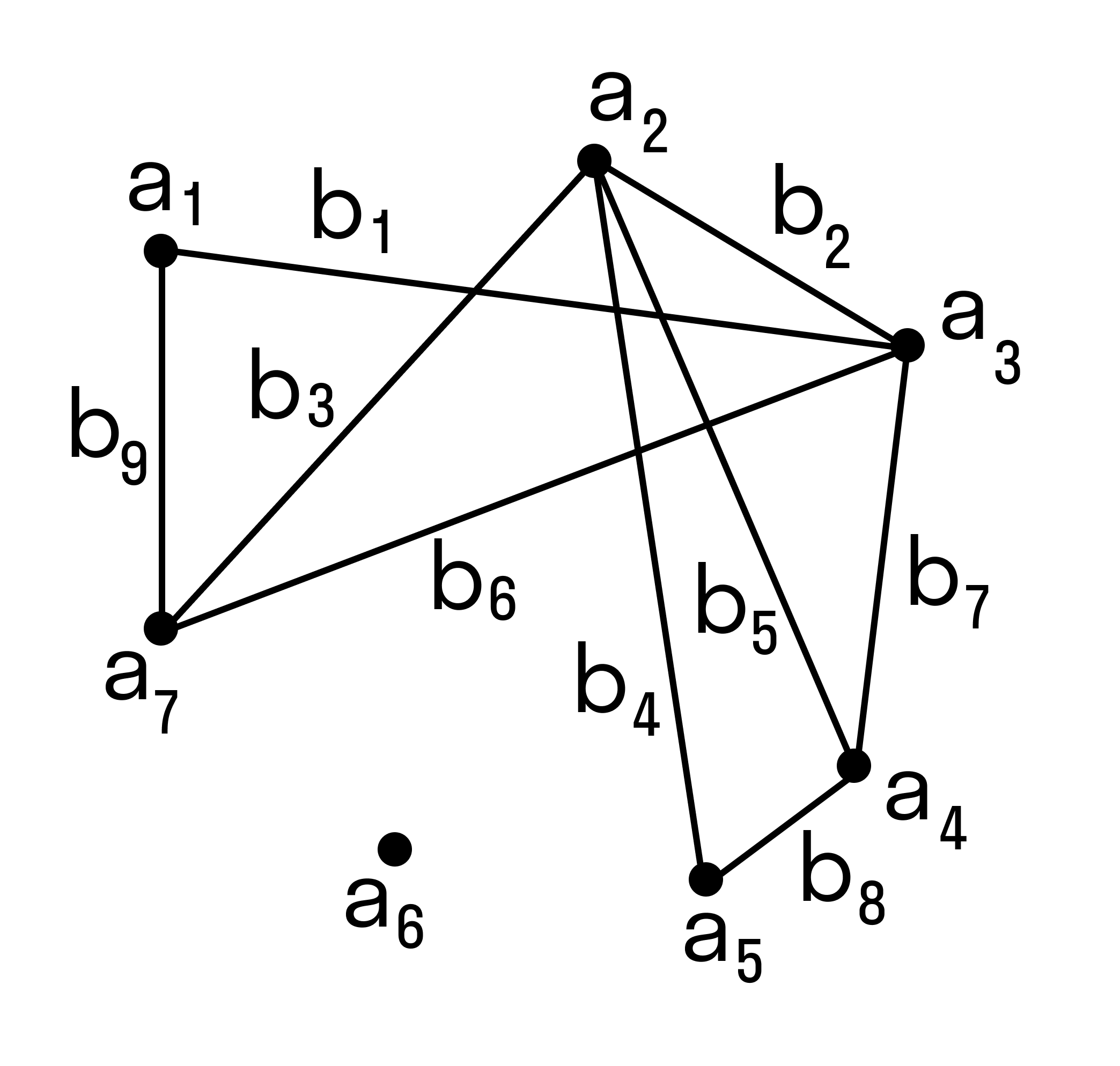
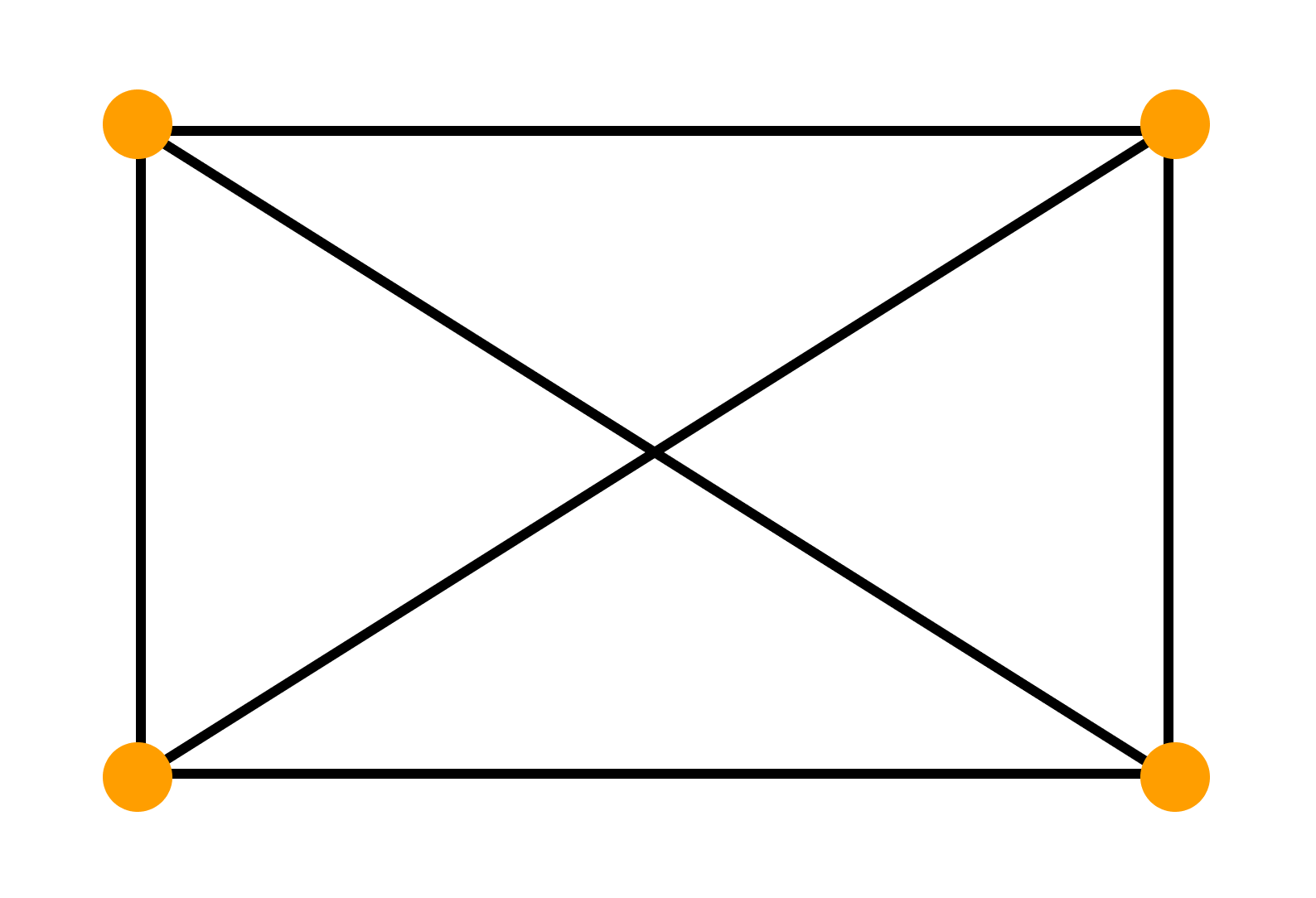
Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.
Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.
Визуализация графовых моделей
Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.
Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.
Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.
Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.
Виды изобразительных соглашений:
Виды графов
Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.
Ориентированные и неориентированные графы
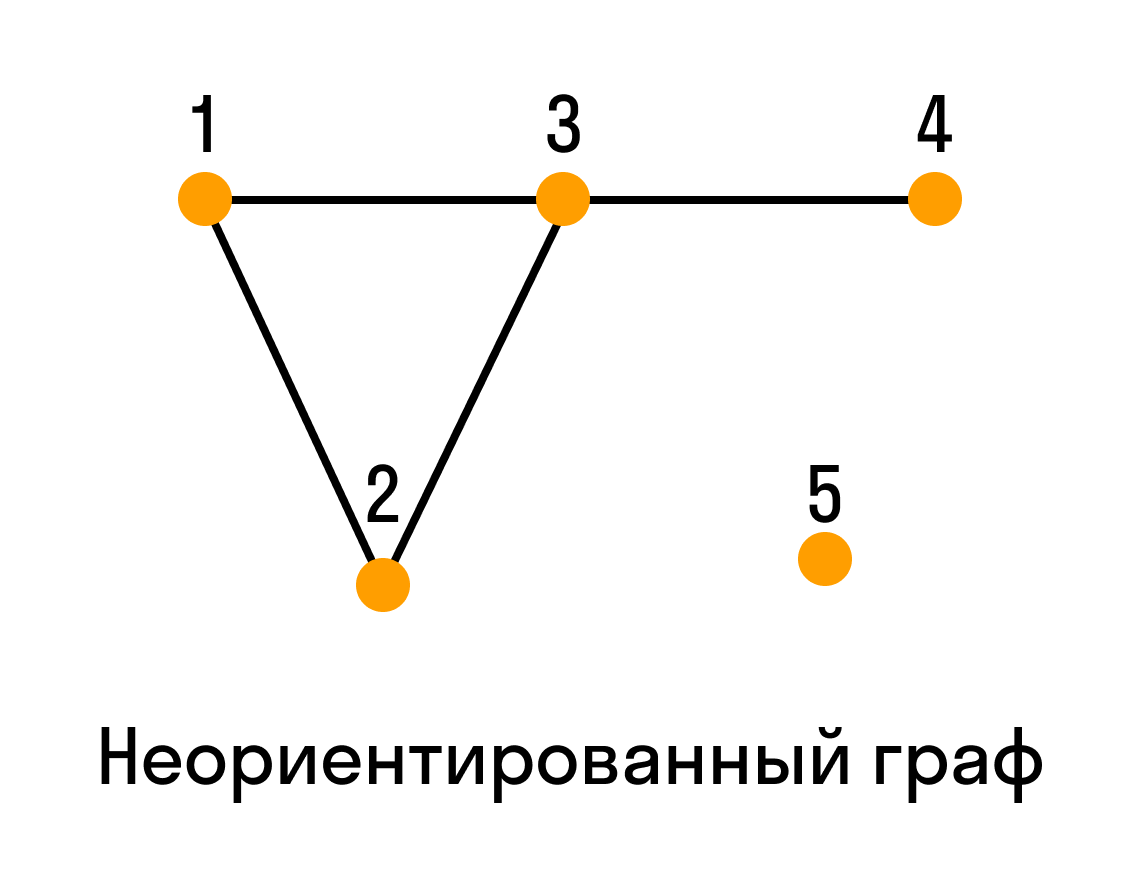
Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.
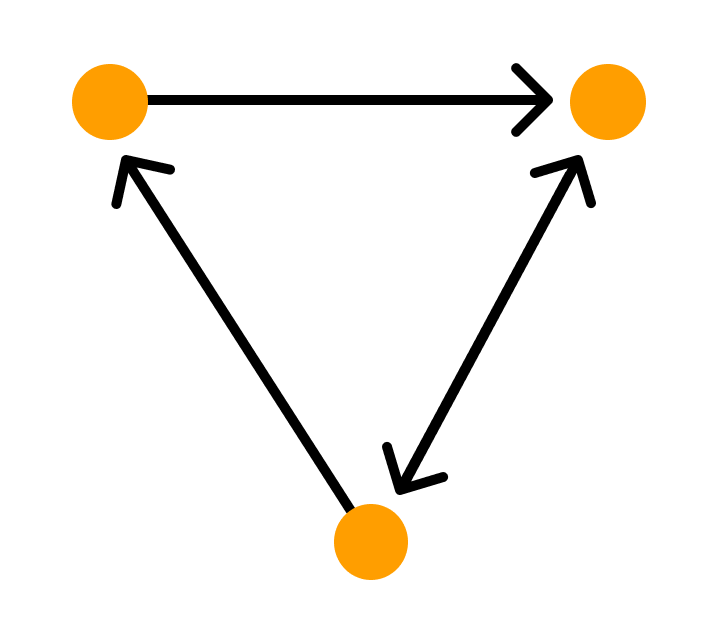
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.
Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.
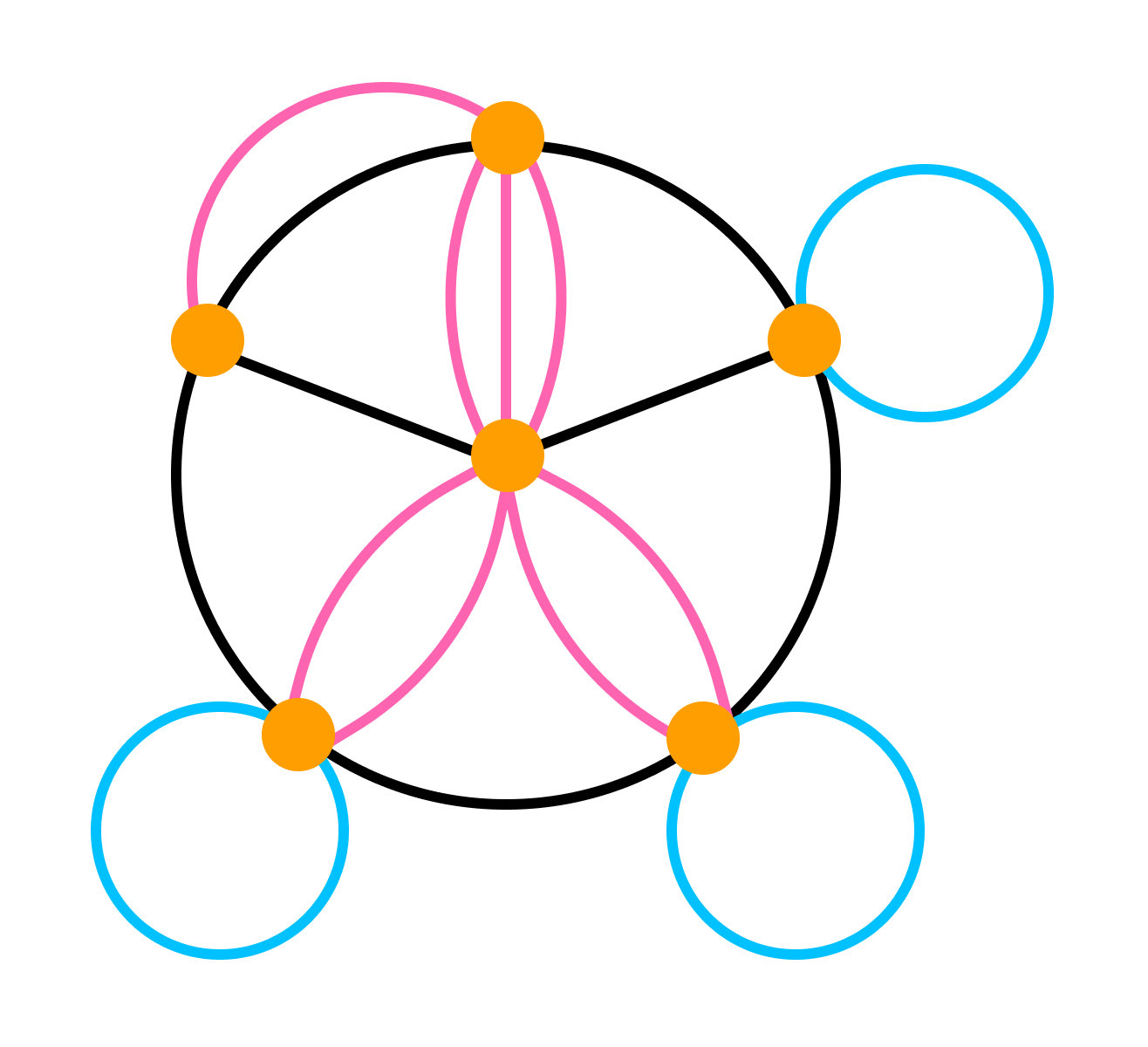
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».
Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).
Пустой граф — это тот, что состоит только из голых вершин.
Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.
Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.
Двудольный граф
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.
Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.
Эйлеров граф
Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?
Регулярный граф
Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.
Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.
Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.
Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.
Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:
Гамильтонов граф
Гамильтоновым графом называется граф, содержащий гамильтонов цикл.
Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.
Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.
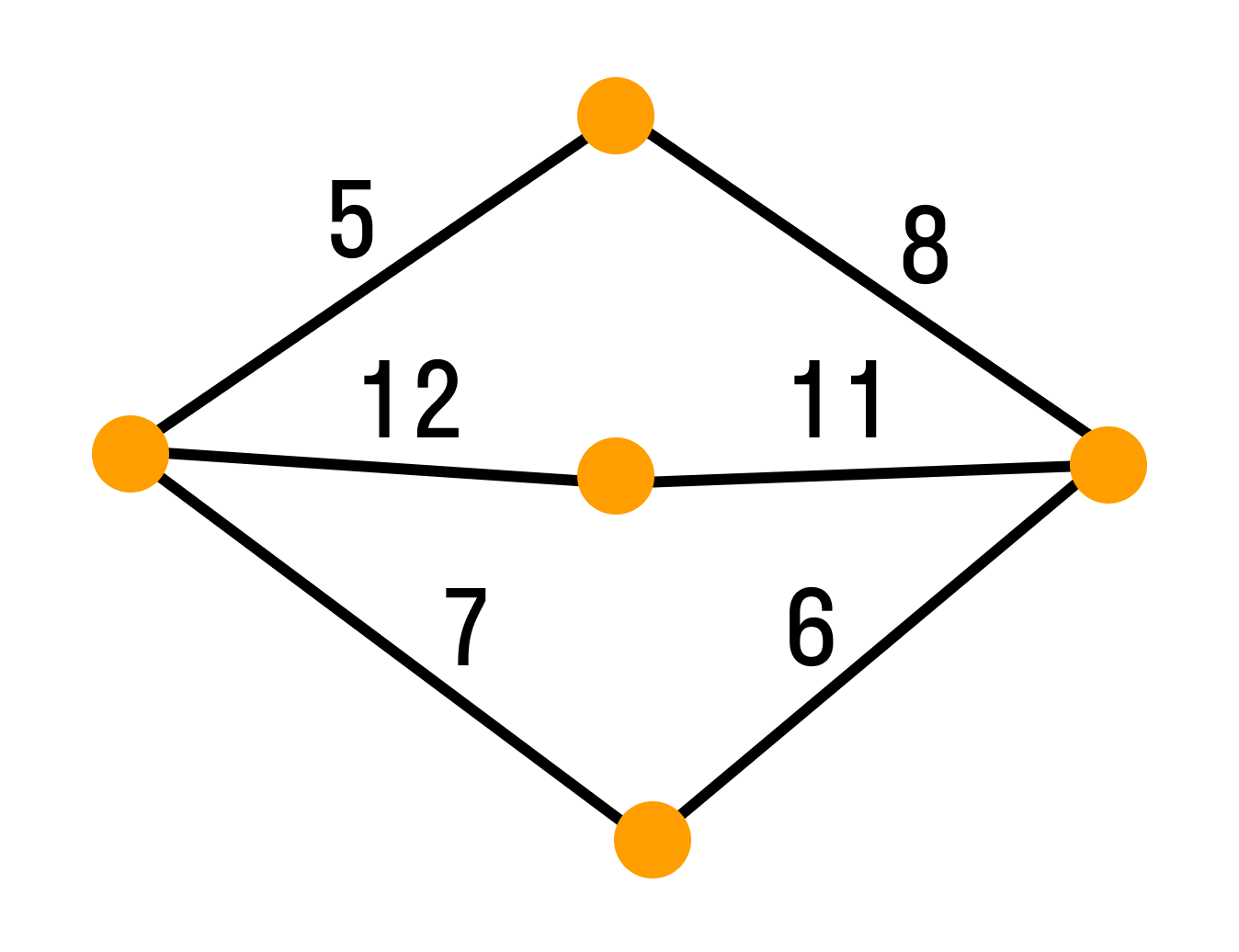
Взвешенный граф
Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.
Графы-деревья
Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.
Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.
Определение дерева
Деревом называется связный граф, который не содержит циклов.
Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.
Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.
Простым путем называется путь, в котором никакое ребро не встречается дважды.
Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:
Дерево — минимальный по числу рёбер связный граф.
Висячей вершиной называется вершина, из которой выходит ровно одно ребро.
Определения дерева:
Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.
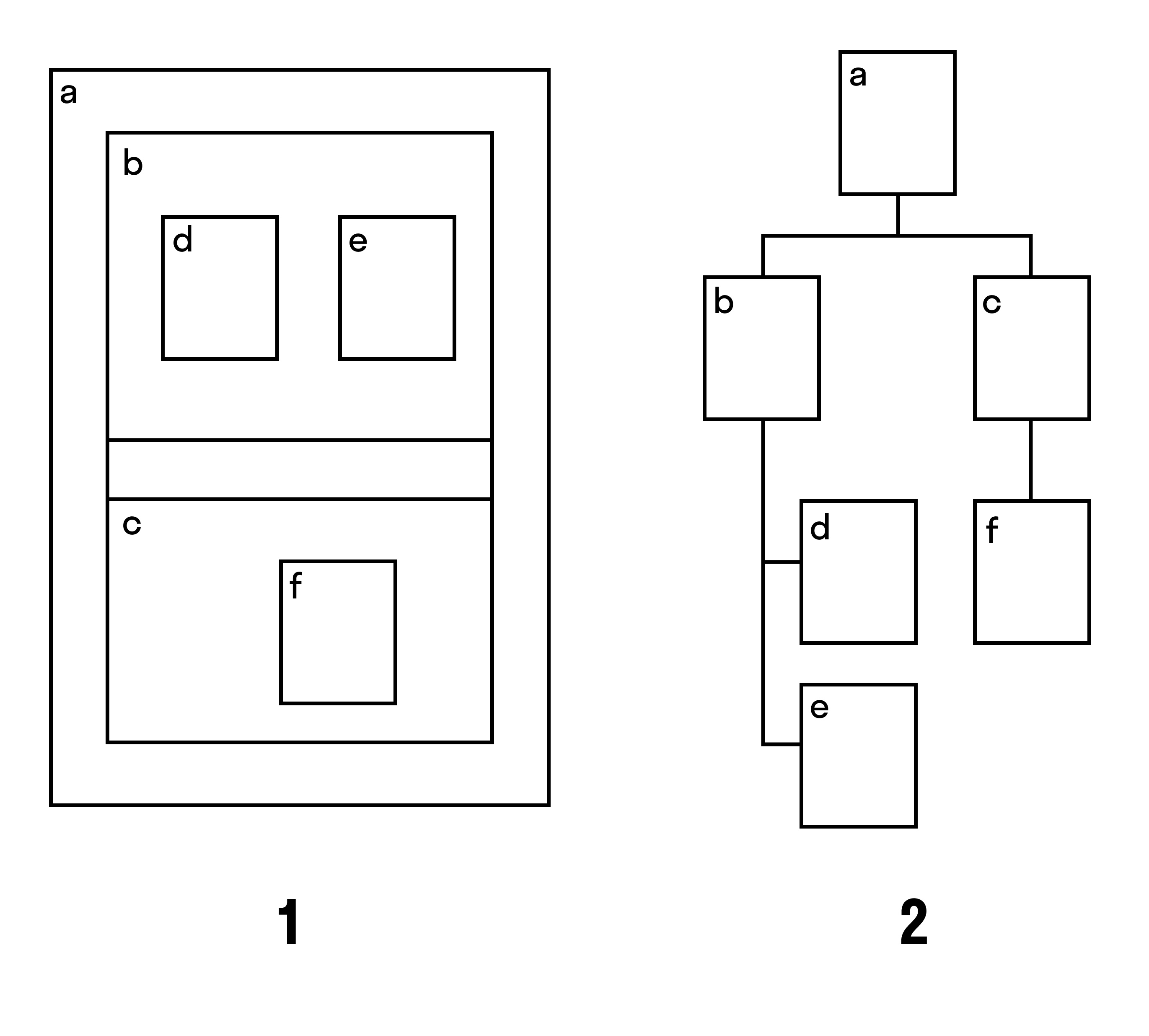
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.
Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:
Теоремы дерева и их доказательства
В дереве с более чем одной вершиной есть висячая вершина.
Доказательство первой теоремы:
Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.
Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.
В дереве число вершин на 1 больше числа ребер.
Доказательство второй теоремы:
Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n