гладкая упругая шайба радиуса r упруго сталкивается с такой же шайбой

Гладкая упругая шайба радиуса r упруго сталкивается с такой же шайбой

Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. е. на тела, входящие в систему, не действуют внешние силы, либо замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. Обращение к сохранению энергии требует порой учёта различных форм внутренней энергии.

Можно сказать, что действие законов сохранения импульса и энергии в процессах столкновения подтверждено широким спектром опытных данных.

Неупругие столкновения

Частица массой `m` с кинетической энергией `K` сталкивается с неподвижной частицей массой `M`. Найдите приращение `Q` внутренней энергии системы частиц в результате абсолютно неупругого столкновения («слипания»).

По закону сохранения энергии

Из приведённых соотношений находим

Отметим, что в предельных случаях

Как видим, при неупругом столкновении лёгкой частицы с массивной (например, электрона с атомом) происходит почти полный переход её кинетической энергии во внутреннюю энергию массивной частицы.

При равенстве масс `(m = M)` `Q = K/2`.

Отсюда следует, например, что при столкновении двух одинаковых ав­томобилей, один из которых неподвижен, а другой движется по на­правлению к нему, половина кинетической энергии идёт на разруше­ние.

Упругие столкновения

Задачу рассмотрим в ЛСО, ось `Ox` которой направим по линии центров шаров в момент соударения. Внешние силы, действующие на шары в процессе соударения, это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Следовательно, импульс системы шаров в процессе взаимодействия не изменяется. По закону сохранения импульса

`m vec v = m vecv_1 + M vecv_2`.

Переходя к проекциям на ось `Ox`, получаем

здесь учтено, что направление скорости налетающего шара после соударения не известно. По закону сохранения энергии

Полученные соотношения перепишем в виде

Налетающий шар будет двигаться после соударения в прежнем направ­лении `(v_(1x) > 0)` при `m > M`, т. е. если масса налетающего шара больше массы по­коящегося шара.

Две гладкие упругие круглые шайбы движутся поступательно по гладкой горизонтальной поверхности. Скорости `vecv_1` и `vecv_2` шайб непосредственно перед соударением известны и показаны на рис. 11. Найдите скорости `vecv_(1)^’` и `vecv_(2)^’` шайб после абсолютно упругого нецентрального соударения. Массы шайб `m_1` и `m_2`.

Задачу рассмотрим в ИСО, оси координат `Ox` и `Oy` которой лежат в горизонтальной плоскости, при этом ось `Ox` направлена по линии центров шайб в момент соударения (рис. 11).

В течение времени соударения на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется:

`vecp_1 + vecp_2 = vecp_(1)^’ + vecp_(2)^’`,

т. е. в проекции на ось `Oy` скорости шайб в результате соударения не изменились.

Найдём `x`-составляющие скоростей шайб после упругого соударения. При таком соударении сохраняется кинетическая энергия

`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x)^’)^2 + (v_(1y)^’)^2))/2 + (m_2 ((v_(2x)^’)^2 + (v_(2y)^’)^2))/2`.

С учётом равенства `y`-составляющих скоростей шайб до и после со­ударения последнее равенство принимает вид:

`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^’)^2)/2 + (m_2 (v_(2x)^’)^2)/2`.

Обратимся к закону сохранения импульса и перейдём к проекциям им­пульсов шайб на ось `Ox`:

`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^’ + m_2 v_(2x)^’`.

`v_(1x) + v_(1x)^’ = v_(2x) + v_(2x)^’`.

Решая систему из двух последних уравнений, находим

Полученные соотношения для `v_(1x)^’`, `v_(1y)^’` и `v_(2x)^’`, `v_(2y)^’` решают вопрос о проекциях и величинах скоростей шайб после соударения

а также об углах `alpha_1` и `alpha_2`, которые векторы скорости `vecv_(1)^’` и `vecv_(2)^’` образуют с положительным направлением оси `Ox`,

`bbb»tg» alpha_1 = (v_(1y)^’)/(v_(1x)^’)`, `bbb»tg» alpha_2 = (v_(2y)^’)/(v_(2x)^’)`.

Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц). Приведём пример.

Воспользуемся результатами, полученными в предыдущем примере. В ЛСО, ось `Ox` которой направлена по линии центров шайбы и обруча в момент соударения, проекции скоростей шайбы и центра обруча на ось `Ox` после соударения равны соответственно

Из этих соотношений следует, что в системе отсчёта, связанной с обручем, проекция скорости шайбы на линию центров после соударения

просто изменила знак, а перпендикулярная линии центров составляющая, как было показано, в рассматриваемом соударении не изменяется. Следовательно, в системе, связанной с обручем, шайба отразится по закону «угол падения равен углу отражения», и минимальное расстояние от шайбы до центра обруча снова будет равно `R//2`. Искомое время

`tau = (R cos^(2) pi/6)/|v_(1xsf»отн»)| = cos pi/6 R/v = sqrt3/2 R/v`.

Источник

Гладкая упругая шайба радиуса r упруго сталкивается с такой же шайбой

С2-1. На космическом аппарате, находящемся вдали от Земли, начал работать реактивный двигатель. Из сопла ракеты ежесекундно выбрасывается 2 кг газа (Δ m/Δt = 2 кг/с) со скоростью v = 500 м/с. Исходная масса аппарата М = 500 кг. Какую скорость приобретет аппарат, пройдя расстояние S = 36 м? Начальную скорость аппарата принять равной нулю. Изменением массы аппарата за время движения пренебречь.

С2-2.На краю стола высотой h = 1,25 м лежит пластилиновый шарик массой m = 100 г. На него со стороны стола налетает по горизонтали другой пластилиновый шарик, имеющий скорость υ = 0,9 м/с. Какой должна быть масса второго шарика, чтобы точка приземления шариков на пол была дальше от стола, чем заданное расстояние L = 0,3 м? (Удар считать центральным.)

С2-3. На гладкой горизонтальной плоскости покоится длинная доска массой М = 2 кг. На доске лежит шайба массой m = 0,5 кг. В начальный момент времени шайбе щелчком сообщили скорость v₀ = 2 м/с. Коэффициент трения между шайбой и доской μ = 0,2. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?

С2-4. На гладкой горизонтальной плоскости находится длинная доска массой M = 2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы v₀ = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?

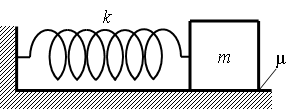
С2.5. На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы v₀ = 2 м/с, а доска покоится. В момент t = 0,8 с шайба перестает скользить по доске. Чему равна масса шайбы m?

А22-1.Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в неподвижно висящий на нити груз массой 81 г, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова длина нити?

А22-2.Летящая горизонтально пластилиновая пуля массой 9 г попадает в неподвижно висящий на нити длиной 40 см груз массой 81 г, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом α = 60°. Какова скорость пули перед попаданием в груз?

А22-3.Перед ударом два пластилиновых шарика движутся взаимно перпендикулярно с одинаковыми импульсами 1 кг•м/с. Массы шариков 100 г и 150 г. После столкновения слипшиеся шарики движутся поступательно. Их общая кинетическая энергия после соударения равна

С1-1. После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме. В некоторый момент времени льдинка находилась в точке А с координатой х = 10 см и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

С1-1. После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме. В некоторый момент времени льдинка находилась в точке А с координатой х = 10 см и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

С1-2. После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от ее координаты в яме. В некоторый момент времени льдинка находилась в точке А с координатой х = 50 см и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

С2-3. К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости μ = 0,2. Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.

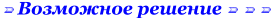
С2-3. Пуля летит горизонтально со скоростью v₀ = 150 м/с, пробивает стоящий на горизонтальной поверхности льда брусок и продолжает движение в прежнем направлении со скоростью V₀/3. Масса бруска в 10 раз больше массы пули. Коэффициент трения скольжения между бруском и льдом μ = 0,1. На какое расстояние S сместится брусок к моменту, когда его скорость уменьшится на 10%?

С2-4.Пуля летит горизонтально со скоростью v₀ = 160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью V₀/4. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью μ= 0,3. На какое расстояние S переместится коробка к моменту, когда её скорость уменьшится на 20%?

С2-5. Брусок массой m₁ = 500 г соскальзывает по наклонной плоскости с высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m ₂ = 300 г. В результате абсолютно неупругого соударения общая кинетическая энергия брусков становится равной 2,5 Дж. Определите высоту наклонной плоскости h. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

С2-6. Брусок массой m₁ = 500 г соскальзывает по наклонной плоскости с высоты h = 0,8 м и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m ₂ = 300 г. Считая столкновение абсолютно неупругим, определите общую кинетическую энергию брусков после столкновения. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

С2.7. Брусок массой m₁ = 500 г соскальзывает по наклонной плоскости высотой h = 0,8 м и сталкивается с неподвижным бруском массой m₂ = 300 г, лежащим на горизонтальной поверхности. Считая столкновение упругим, определите кинетическую энергию первого бруска после столкновения. Трением при движении пренебречь.

С2.9. Брусок массой m скользит по горизонтальной поверхности стола и нагоняет брусок массой 6m, скользящий по столу в том же направлении. В результате неупругого соударения бруски слипаются. Их скорости перед ударом были v₀ = 7 м/с и v₀/3. Коэффициент трения скольжения между брусками и столом μ = 0,5. На какое расстояние переместятся слипшиеся бруски к моменту, когда их скорость станет 2v₀/7?

С2-11. Шайба массой m = 100 г начинает движение по желобу АВ из точки А из состояния покоя. Точка А расположена выше точки В на высоте Н = 6 м. В процессе движения по желобу механическая энергия шайбы из-за трения уменьшается на ΔE = 2 Дж. В точке В шайба вылетает из желоба поз углом α = 15 0 к горизонту и падает на землю в точке D. находящейся на одной горизонтали с точкой В (см. рисунок). Найдите BD. Сопротивлением воздуха пренебречь.

С2-12. Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рисунок). В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит v₀ = 4 м/с, то в точке В шайба отрывается от опоры. Длина наклонной плоскости АВ = L = 1 м, угол α = 30°. Коэффициент трения между наклонной плоскостью и шайбой μ = 0,2. Найдите внешний радиус трубы R.

С2.13. Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закреплённого кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?

С2.14.Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закреплённой сферы. Груз m находится в точке А на вершине сферы (см. рисунок). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу М, если m = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.

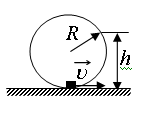
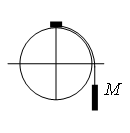
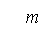
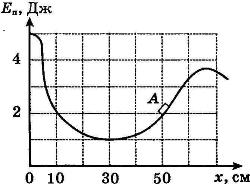
С2.15.Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закреплённого кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?

С2-16. Кусок пластилина сталкивается с покоящимся на горизонтальной поверхности стола бруском и прилипает к нему. Скорость пластилина перед ударом равна v_пл = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ = 0,25. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 40%?

С2.17. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно и равны v_пл = 15 м/с и v_бр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ = 0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?

С2-18. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены взаимно противоположно и равны v _пл =15 м/с и v_бр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ = 0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится в 2 раза?

С2-19. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены взаимно противоположно и равны v _пл = 15 м/с и v _бр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. К моменту, когда скорость слипшихся бруска и пластилина уменьшилась в 2 раза, они переместились на 0,22 м. Определите коэффициент трения μ бруска о поверхность стола.

С2-20. Пуля летит горизонтально со скоростью v₀ = 150 м/с, пробивает стоящий на горизонтальной поверхности льда брусок и продолжает движение в прежнем направлении со скоростью v₀/3. Масса бруска в 10 раз больше массы пули. Коэффициент трения скольжения между бруском и льдом μ = 0,1. На какое расстояние S сместится брусок к моменту, когда его скорость уменьшится на 10%?

С2.21. Пуля, летящая горизонтально со скоростью v_o = 120 м/с, пробивает лежащую на горизонтальной поверхности стола коробку и продолжает движение в прежнем направлении, потеряв 80% скорости. Масса коробки в 16 раз больше массы пули. Коэффициент трения скольжения между коробкой и столом μ = 0,5. На какое расстояние переместится коробка к моменту, когда её скорость уменьшится вдвое?

С2.24. Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?

С2.25. Каково среднее давление пороховых газов в стволе орудия, если скорость вылетевшего из него снаряда равна 1,5 км/с? Длина ствола 3 м, его диаметр 45 мм, масса снаряда 2 кг. (Трение пренебрежимо мало.)

С2-26. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок). На краю трамплина скорость гонщика направлена под таким углом к горизонту, что дальность его полёта максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

С2-27. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 30° к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова дальность полета L на этом трамплине? Сопротивлением воздуха и трением пренебречь.

С2-28. При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземлился на горизонтальный стол на той же высоте, что и край трамплина. Каково время полета?

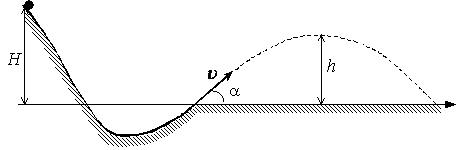
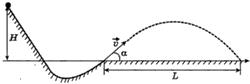
С2-29. Шарик скользит без трения по наклонному желобу, а затем движется по «мертвой петле» радиуса R. С какой силой давит шарик на желоб в верхней точке петли, если масса шарика 100 г, а высота, с которой его отпускают, равна 4 R считая от нижней точки петли?

Источник