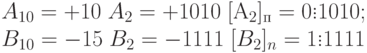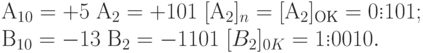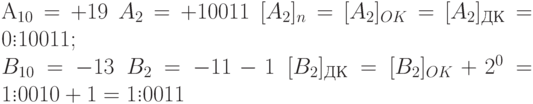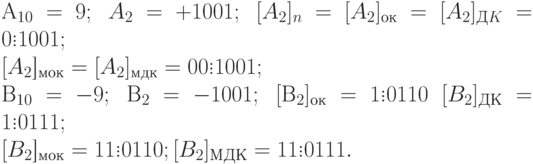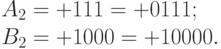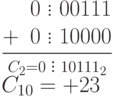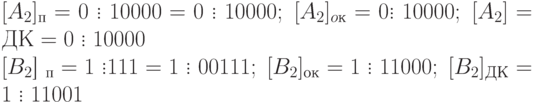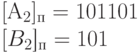числовая система эвм операции над машинными кодами

Арифметические основы ЭВМ. Машинные коды, операции с ними

6. Арифметические основы ЭВМ. Машинные коды, операции с ними

Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Но выполнение любой операции основано на использовании простейших микроопераций типа сложения и сдвиг. Это позволяет иметь единое арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации.

Под знак чисел отводится специальный знаковый разряд. Знак «+» кодируется двоичным нулем, а знак «–» – единицей.

В ЭВМ все операции выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.

Различают прямой код (П), обратный код (ОК) и дополнительный код (ДК) двоичных чисел.

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.

Вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд от значащих.

Обратный код двоичного числа образуется по следующему правилу.

Обратный код положительных чисел совпадает с их прямым кодом.

Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы – нулями.

Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа А>=О и В>=О, тогда операция алгебраического сложения выполняется в соответствии с табл.

Умножение. Умножение двоичных чисел наиболее просто реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.

Операция деления, как и в десятичной арифметике, является обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.

7. Алгебра логики. Булевы функции, способы задания

Алгебра логики – устанавливает основные законы формирования и преобразования логических функций. Она позволяет представить любую сложную функцию в виде композиции простейших функций.

Существует несколько синонимов по отношению к функциям алгебры логики:

• функции алгебры логики (ФАЛ);

Вся информация в ЭВМ представляется в двоичной системе счисления. Поставим в соответствие входным сигналам отдельных устройств ЭВМ соответствующие значения х_i, (i=1, n), а выходным сигналам – значения функций у_j(j=1, m)

где х_i— i-й вход; n – число входов; у_j – j – й выход; m – число выходов в устройстве, описывают алгоритм работы любого устройства ЭВМ.

Каждая такая зависимость y_j, является «булевой функцией» (функцией алгебры логики) – число возможных состояний её и каждой её независимой переменной равно двум, а её аргументы определены на множестве <0,1>.

Способы представления ФАЛ

При этом способе словесное описание однозначно определяет все случаи, при которых функция принимает значения 0 или 1. Например, многовходовая функция ИЛИ может иметь такое словесное описание: функция принимает значение 1, если хотя бы один из аргументов принимает значение 1, иначе – 0.

Функция задается в виде десятичных (или восьмеричных, или шестнадцатиричных) эквивалентов номеров тех наборов аргументов, на которых функция принимает значение 1.

Условие, что функция f (x1, x2, x3) = 1 на наборах 1,3,5,6,7 записывается f (1, 3, 5, 6, 7) = 1.

Аналогичным образом булева функция может быть задана по нулевым значениям.

Функция задается в виде таблицы истинности (соответствия), которая содержит 2 n строк (по числу наборов аргументов), n столбцов по числу переменных и один столбец значений функции. В такой таблице каждому набору аргументов соответствует значение функции.

Функция задается в виде алгебраического выражения, получаемого путем применения каких-либо логических операций к переменным алгебры логики. применяя операции конъюнкции и дизъюнкции можно задать функцию выражением f (x1, x2, x3) = x1x2 v x3.

При этом способе задания таблица истинности функции представляется в виде координатной карты состояний, которая часто называется картой Карно. Такая карта содержит 2 n клеток по числу наборов всевозможных значений n переменных функции. Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца, а другая – координаты строки.

При такoм способе построения клетка определяется координатами переменных, соответствующих определенному двоичному набору.

Внутри клетки карты Карно ставится значение функции на данном наборе.

Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е. были соседними.

Такой способ представления очень удобен для наглядности при минимизации булевых функций.

Является способом представления функционирования схемы, реализующей булеву функцию, во времени. Изображается в виде системы графиков, у которых ось Х соответствует автоматному времени (моментам времени), а ось Y соответствует напряжению дискретных уровней сигналов «логический 0» (0,4 в) и «логическая 1» (2,4 в).

Функция задается в виде n-мерного единичного куба, вершинам которого соответствуют наборы значений аргументов и приписаны значения функции на этих наборах. Куб назван единичным, так как каждое ребро соединяет вершины, наборы которых различаются только по одной переменной, т.е. являются соседними.

Такой способ задания булевых функций иногда называют геометрическим, но чаще всего кубическим. Кубическое представление наиболее пригодно для машинных методов анализа булевых функций, так как позволяет компактно представлять булевы функции от большого количества переменных.

Источник

Информационно-логические основы ЭВМ

Машинные коды

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.

Точечной вертикальной линией здесь отмечена условная граница, отделяющая знак от цифровых разрядов.

Свое название обратный код чисел получил потому, что коды цифр отрицательного числа заменены инверсными. Укажем наиболее важные свойства обратного кода чисел:

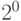
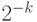
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (— для целых чисел, — для дробных).

Укажем основные свойства дополнительного кода.

Сложение дополнительных кодов положительного числа с его отрицательным значением дает так называемую машинную единицу дополнительного кода:

т. е. число 10 (два) в знаковых разрядах числа.

Арифметические операции над числами с фиксированной точкой

Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный ( ОК ) или дополнительный (ДК) код. Пусть числа 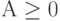и , тогда операция алгебраического сложения выполняется в соответствии с табл. 14.3.

Таблица 14.3. Таблица преобразования кодов при алгебраическом сложении

Требуемая операция	Необходимое преобразование

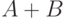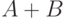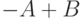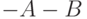Зависимости, представленные в правой части таблицы, указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 14.2. При выполнении сложения цифр необходимо соблюдать следующие правила.

Пример 14.9. Сложить два числа .

Исходные числа имеют различную разрядность, и необходимо провести выравнивание разрядной сетки:

Сложение в обратном или дополнительном кодах дает один и тот же результат:

Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.

Пример 14.10. Сложить два числа 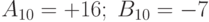в ОК и ДК. В соответствии с табл. 14.3 должна быть реализована зависимость , в которой второй член преобразуется с учетом знака

При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см. п. 4. правил). В случае ДК этот перенос игнорируется.

Умножение. Умножение двоичных чисел наиболее просто реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.

Пример 14.11. Умножить два числа 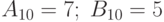. Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.

Нетрудно видеть, что произведение получается путем сложения частных произведений, которые представляют собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль, игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до . Знак произведения формируется путем сложения знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.

Деление. Операция деления, как и в десятичной арифметике, является обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.

Пример 14.12. Разделить два числа .

Знак частного формируется также путем сложения знаковых разрядов делимого и делителя, как это делалось при умножении.

Источник

1.3. Операции над машинными кодами чисел

Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Однако выполнение любой операции основано на использовании простейших микроопераций типа сло­жения и сдвиг. Это позволяет иметь единое арифметико-логическое устрой­ство для выполнения любых операций, связанных с обработкой информа­ции. Правила сложения двоичных цифр двух чисел А и В представлены в табл. 1.4.

Здесь показаны правила сложения двоичных цифр a_i, b_i одноименных раз­рядов с учетом возможных переносов из предыдущего разряда p_i-1.

Перенос в следующий разряд

• во-первых, приходится отдельно обрабатывать значащие разряды чисел и разряды знака;

• во-вторых, значение разряда знака влияет на алгоритм выполнения опе­рации (сложение может заменяться вычитанием и наоборот).

Во всех ЭВМ без исключения все операции выполняются над числами, представленными специальными машинными кодами. Их использование по­зволяет обрабатывать знаковые разряды чисел так же, как и значащие раз­ряды, а также заменять операцию вычитания операцией сложения.

Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа А≥0 и В≥0, тогда операция алгебраического сложения выпол­няется в соответствии с табл. 1.5.

Таблица преобразования кодов при алгебраическом сложении

Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом со­ответствующего числа. Сложение двоичных чисел осуществляется после­довательно, поразрядно в соответствии с табл. 1.4. При выполнении сложе­ния с использованием машинных кодов необходимо соблюдать следующие правила.

1. Слагаемые должны иметь одинаковое число разрядов. Для выравни­вания разрядной сетки слагаемых можно дописывать нули слева к целой части числа и нули справа к дробной части числа.

2. Знаковые разряды чисел участвуют в сложении так же, как и значащие.

3. Необходимые преобразования кодов (п.1.2.) производятся с измене­нием знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.

4. При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса отбрасывается. Знак результа­та формируется автоматически, результат представляется в том коде, в кото­ром представлены исходные слагаемые.

Исходные числа имеют различную разрядность, необходимо провести выравни­вание разрядной сетки:

Сложение в обратном или дополнительном коде дает один и тот же результат 0.00111

Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый раз­ряд и из знакового разряда, что свидетельствует о получении правильного результата.

В соответствии с табл. 1.5 должна быть реализована зависимость А+(-В), в кото­рой второе слагаемое преобразуется с учетом знака

[A₂]пк = 0.10000 = 0.10000 [А₂]ок = 0.10000 [А₂]дк = 0.10000;

[B₂]пк = 1.00111 = 1.00111 [В₂]ок = 1.11000 [В₂]дк = 1.11001.

Сложение в OK Сложение в ДК

При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см.п.4 правил). В случае ДК этот перенос игнорируется.

Пример 1.19. Сложить два числа А₁₀ =- 16 В= +7 в ОК и ДК.

В соответствии с табл. 1.3 должна быть реализована зависимость

(-А)+В, в кото­рой первое слагаемое преобразуется с учетом знака

[B₂]пк = + 00111= 0.00111 [В₂]ок = 0.00111 [В₂]дк = 0.00111.

Сложение в OK Сложение в ДК

При сложении чисел в ОК и ДК были получены отрицательные результаты («1» в знаковом разряде). Для перевода обратного кода отрицательного числа в прямой необходимо инвертировать значащие разряды, а знаковый разряд оставить без изменения. А для перевода дополнительного кода отрицательного числа в прямой код необходимо инвертировать значащие разряды и прибавить единицу младшего разряда.

т.о. имеем в ПК из ОК 1.01001, а в ПК из ДК 1.01000

Умножение. Умножение двоичных чисел реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.

Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.

+ 111 – мл. разряд ОП2 равен «1», поэтому к РЧС +ОП1;

1 такт  = 111 – результирующее значение РЧС;

 0111 – сдвиг РЧС вправо на один разряд;

2 такт  = 00111 –очередной р-д ОП2=«0», поэтому только сдвиг

Знак произведения определяется путем сложения по «модулю 2» знаков сомножителей ( 0  0 = 0)

Нетрудно видеть, что произведение получается путем сложения част­ных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведе­ния, полученные умножением на нуль, игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение раз­рядности произведения до п+п=2п. Знак произведения формируется путем сложения по модулю «2» знаковых разрядов сомножителей. Возможные переносы из знако­вого разряда игнорируются.

Деление. Операция деления, как и в десятичной арифметике, является обратной операции умножения. Эта операция также приводится к последовательности операций сложения и сдвига.

Отметим, что делимое перед операцией деления должно быть приведено к 2n-разрядной сетке. Только в этом случае при делении на n-разрядный делитель получается n-разрядное частное.

Знак частного формируется также путем сложения по «модулю 2» знаковых разрядов делимого и делителя, как это делалось при умножении.

Признаками переполнения являются:

наличие переноса из значащих разрядов в знаковый и отсутствие переноса из знакового разряда («положительное» переполнение);

наличие переноса из знакового разряда и отсутствие переноса из значащих в знаковый разряд («отрицательное» переполнение).

Пример 1.21. Сложить 2 числа: А=+5 и В=+6 в четырехразрядной сетке (с учетом знакового разряда).

Сложение в OK Сложение в ДК

Сложить 2 числа: А=-5 и В=-6 в четырехразрядной сетке (с учетом знакового разряда).

Сложение в OK Сложение в ДК

Как видно из примеров, при сложении положительных чисел получается отрицательный результат и наоборот. Это объясняется тем, что в трех значащих разрядах максимальное число по модулю может быть семь, а в примерах необходимо записать соответственно С=+11 и С=-11.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Арифметические основы ЭВМ. Машинные коды, операции с ними

Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Но выполнение любой операции основано на использовании простейших микроопераций типа сложения и сдвиг. Это позволяет иметь единое арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации.

Под знак чисел отводится специальный знаковый разряд. Знак «+» кодируется двоичным нулем, а знак «–» – единицей.

В ЭВМ все операции выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.

Различают прямой код (П), обратный код (ОК) и дополнительный код (ДК) двоичных чисел.

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.

Вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд от значащих.

Обратный код двоичного числа образуется по следующему правилу.

Обратный код положительных чисел совпадает с их прямым кодом.

Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы – нулями.

Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа А>=О и В>=О, тогда операция алгебраического сложения выполняется в соответствии с табл.

Умножение. Умножение двоичных чисел наиболее просто реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.

Операция деления, как и в десятичной арифметике, является обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.

Алгебра логики. Булевы функции, способы задания

Алгебра логики – устанавливает основные законы формирования и преобразования логических функций. Она позволяет представить любую сложную функцию в виде композиции простейших функций.

Существует несколько синонимов по отношению к функциям алгебры логики:

• функции алгебры логики (ФАЛ);

где х _i — i-й вход; n – число входов; у _j – j – й выход; m – число выходов в устройстве, описывают алгоритм работы любого устройства ЭВМ.

Способы представления ФАЛ

Словесный

При этом способе словесное описание однозначно определяет все случаи, при которых функция принимает значения 0 или 1. Например, многовходовая функция ИЛИ может иметь такое словесное описание: функция принимает значение 1, если хотя бы один из аргументов принимает значение 1, иначе – 0.

Числовой

Функция задается в виде десятичных (или восьмеричных, или шестнадцатиричных) эквивалентов номеров тех наборов аргументов, на которых функция принимает значение 1.

Условие, что функция f (x1, x2, x3) = 1 на наборах 1,3,5,6,7 записывается f (1, 3, 5, 6, 7) = 1.

Аналогичным образом булева функция может быть задана по нулевым значениям.

Табличный

Функция задается в виде таблицы истинности(соответствия), которая содержит 2 n строк (по числу наборов аргументов), n столбцов по числу переменных и один столбец значений функции. В такой таблице каждому набору аргументов соответствует значение функции.

Аналитический

Функция задается в виде алгебраического выражения, получаемого путем применения каких-либо логических операций к переменным алгебры логики. применяя операции конъюнкции и дизъюнкции можно задать функцию выражением f (x1, x2, x3) = x1x2 v x3.

Координатный

При этом способе задания таблица истинности функции представляется в виде координатной карты состояний, которая часто называется картой Карно. Такая карта содержит 2 n клеток по числу наборов всевозможных значений n переменных функции. Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца, а другая – координаты строки.

При такoм способе построения клетка определяется координатами переменных, соответствующих определенному двоичному набору.

Внутри клетки карты Карно ставится значение функции на данном наборе.

Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е. были соседними.

Такой способ представления очень удобен для наглядности при минимизации булевых функций.

Диаграмный

Является способом представления функционирования схемы, реализующей булеву функцию, во времени. Изображается в виде системы графиков, у которых ось Х соответствует автоматному времени (моментам времени), а ось Y соответствует напряжению дискретных уровней сигналов «логический 0» (0,4 в) и «логическая 1» (2,4 в).

Графический

Функция задается в виде n-мерного единичного куба, вершинам которого соответствуют наборы значений аргументов и приписаны значения функции на этих наборах. Куб назван единичным, так как каждое ребро соединяет вершины, наборы которых различаются только по одной переменной, т.е. являются соседними.

Такой способ задания булевых функций иногда называют геометрическим, но чаще всего кубическим. Кубическое представление наиболее пригодно для машинных методов анализа булевых функций, так как позволяет компактно представлять булевы функции от большого количества переменных.

Источник