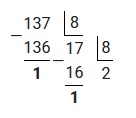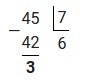число 7 в десятичной системе счисления при переводе его в циклический код имеет вид
Перевод из любой системы счисления в любую
Для перевода чисел из одной системы счисления в любую другую, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода из произвольных чисел в любую систему счисления
Подробно о переводе в десятичную систему смотрите на этой странице, о переводе из десятичной в q-ричную- здесь. Для целостного понимания, разберем несколько примеров, но для начала вспомним алфавиты в популярных системах счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 8 | Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Перевод целого q-ичного числа в систему счисления с новым основанием
Пример 1: перевести число 1101100 из двоичной в троичную систему.
Как было сказано выше, необходимо сначала перевести число в десятичное, а полученный ответ в троиную. Решение будет выглядеть следующим образом:
Для перевода шестнадцатеричного числа 1a316 в десятичную систему, воспользуемся формулой:
11011002=1 ∙ 2 6 + 1 ∙ 2 5 + 0 ∙ 2 4 + 1 ∙ 2 3 + 1 ∙ 2 2 + 0 ∙ 2 1 + 0 ∙ 2 0 = 1 ∙ 64 + 1 ∙ 32 + 0 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 = 64 + 32 + 0 + 8 + 4 + 0 + 0 = 10810
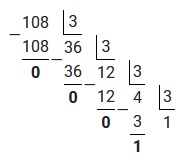
Полученное число 108 переведем из десятичной системы счисления в троичную. Для этого, осуществим последовательное деление на 3, до тех пор пока остаток не будет меньше чем 3.
Полученные остатки записываем в обратном порядке, таким образом:
Пример 2: перевести число 345 из шестеричной в восьмеричную систему.
Аналогично предыдущему примеру произведем вычисления:
3456=3 ∙ 6 2 + 4 ∙ 6 1 + 5 ∙ 6 0 = 3 ∙ 36 + 4 ∙ 6 + 5 ∙ 1 = 108 + 24 + 5 = 13710
Полученное число 137 переведем из десятичной системы счисления в восьмеричную. Для этого, осуществим последовательное деление на 8, до тех пор пока остаток не будет меньше чем 8.
Полученные остатки записываем в обратном порядке, таким образом:
Перевод любого дробного числа из одной системы в другую
Пример 3: перевести 231.20 из четверичной в семеричную систему счисления.
Общий смысл алгоритма перевода дробного числа, аналогичен алгоритму перевода целого, т.е. вначале переводим в десятичную, а затем в семеричную:
1. Для перевода числа 231.20 в десятичную систему воспользуемся формулой:
Обратите внимание! Формула перевода дробного числа в десятичную систему, очень похожа на формулу перевода целого, однако немного отличается.
2. Полученное число 45.5 переведем из десятичной системы счисления в семеричную. Т.к. полученное число содержит дробную часть, нам потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
2.1 Для того, чтобы перевести число 45 из десятичной системы счисления в 7-ую, необходимо осуществить последовательное деление на 7, до тех пор пока остаток не будет меньше чем 7.
Полученные остатки записываем в обратном порядке, таким образом:
2.2 Для перевода десятичной дроби 0.5 в 7-ую систему, необходимо выполнить последовательное умножение дроби на 7, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
0.5 ∙ 7 = 3.5 (3)
Ответом станет прямая последовательность целых частей произведения. Т.е.
2.3. Осталось соединить переведенные части, таким образом:
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.