быстрое преобразование фурье что такое

Быстрое преобразование Фурье

Содержание

Описание задачи [ править ]

Метод основывается на том, что степени одних комплексных корней единицы в степени [math]n[/math] дают другие.

Cначала мы разделяем вектор коэффициентов на два вектора, рекурсивно вычисляем значение ДПФ для них, и объединяем их в одно ДПФ.

Алгоритм построения БПФ [ править ]

[math] A(x) = a_0 x^0 + a_1 x^1 + \ldots + a_ x^ [/math]

Разделим [math]A(x)[/math] на два многочлена, где один будет с четными, а другой с нечетными коэффициентами:

[math] A_0(x) = a_0 x^0 + a_2 x^1 + \ldots + a_ x^<\frac <2>— 1> [/math]

[math] A_1(x) = a_1 x^0 + a_3 x^1 + \ldots + a_ x^<\frac <2>— 1> [/math]

Многочлен [math]A(x)[/math] получается из [math]A_0(x)[/math] и [math]A_1(x)[/math] следующим образом:

[math]A(x) = A_0(x^2) + xA_1(x^2) \ \ \ \ \ (1)[/math]

Таким образом, мы получили:

Алгоритм построения обратного БПФ [ править ]

Рассмотрим ДПФ в матричном виде:

[math] \begin \omega_n^0 & \omega_n^0 & \omega_n^0 & \ldots & \omega_n^0\\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \ldots & \omega_n^ \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \ldots & \omega_n^ <2(n-1)>\\ \vdots& \vdots & \vdots &\ddots & \vdots\\ \omega_n^0 & \omega_n^ & \omega_n^ <2(n-1)>&\ldots & \omega_n^ <(n-1)(n-1)>\end \begin a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_ \end = \begin y_0 \\ y_1 \\ y_2 \\ \vdots \\ y_ \end [/math]

[math] \begin a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_ \end = <\begin\omega_n^0 & \omega_n^0 & \omega_n^0 & \ldots & \omega_n^0\\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \ldots & \omega_n^ \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \ldots & \omega_n^ <2(n-1)>\\ \vdots& \vdots & \vdots &\ddots & \vdots\\ \omega_n^0 & \omega_n^ & \omega_n^ <2(n-1)>&\ldots & \omega_n^ <(n-1)(n-1)>\end>^ <-1>\begin y_0 \\ y_1 \\ y_2 \\ \vdots \\ y_ \end [/math]

Непосредственной проверкой можно убедиться, что обратная матрица имеет вид:

[math] \dfrac<1> \begin \omega_n^0 & \omega_n^0 & \omega_n^0 & \ldots & \omega_n^0\\ \omega_n^0 & \omega_n^ <-1>& \omega_n^ <-2>& \ldots & \omega_n^ <-(n-1)>\\ \omega_n^0 & \omega_n^ <-2>& \omega_n^ <-4>& \ldots & \omega_n^ <-2(n-1)>\\ \vdots& \vdots & \vdots &\ddots & \vdots\\ \omega_n^0 & \omega_n^ <-(n-1)>& \omega_n^ <-2(n-1)>&\ldots & \omega_n^ <-(n-1)(n-1)>\end [/math]

Получаем формулу для [math]a_k[/math] :

Источник

Простыми словами о преобразовании Фурье

Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

(с) xkcd

Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):

Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:

График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).

Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.

Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.

Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:

Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.

Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.

Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.

Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.

Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).

Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:

Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T

Источник

Быстрое преобразование фурье что такое

«Быстрое преобразование Фурье».

Дискретное преобразование Фурье (ДПФ) периодического дискретного сигнала x ( n ) с периодом N определяется как

(12.1),

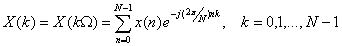
Выражение (12.1) можно переписать в виде

(12.2),

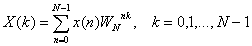
где 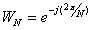(12.3).

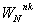
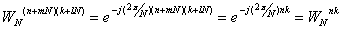
Коэффициент W_N называется поворачивающим множителем. Легко показать, что является периодической функцией с периодом N

(12.4).

Если сравнить ДПФ конечного дискретного сигнала со спектром этого же сигнала, определяемым выражением

(12.5),

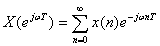
Существует большое количество алгоритмов БПФ. Однако все они являются частными случаями единого алгоритма, базирующегося на задаче разбиения одного массива чисел на два. Тот факт, что это можно сделать более чем одним способом, определяет многообразие алгоритмов БПФ. Расмотрим два из них.

Первый алгоритм называется алгоритмом Б ПФ с пр ореживанием по времени.

Разобъем исходный сигнал x ( n ) на два N /2-отсчетных сигнала x ₁ ( n ) и x ₂ ( n ), составленных соответственно из четных и нечетных отсчетов исходного сигнала x ( n )

(12.6).

(12.7).

(12.8)

(12.9)

(12.10),

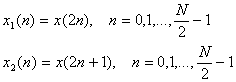
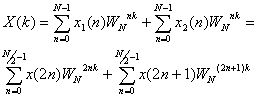
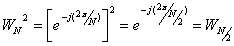
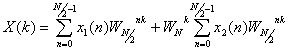
где X ₁ ( k ) и X ₂ ( k ) – N /2-отсчетные ДПФ сигналов x ₁ ( n ) и x ₂ ( n ) соответственно.

(12.11),

(12.12).

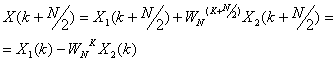
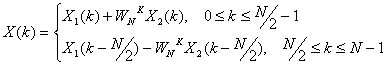
На рис.12.1 представлена последовательность операций при выполнении восьмиточечного ДПФ с использованием двух четырехточечных ДПФ.

Источник

Быстрое преобразование Фурье

Быстрое преобразование Фурье — один из самых важных алгоритмов XX века, если не самый важный.

Оно применяется, как можно догадаться, для вычисления преобразований Фурье, которые в свою очередь используются для обработки звука, электромагнитных волн, задач оптики, сжатия данных, физического моделирования и прочих сложных математических и физических задач.

В этой статье же мы подойдем немного с другой стороны и рассмотрим алгоритм быстрого преобразования Фурье в контексте задачи умножения чисел и многочленов, часто встречающейся в олимпиадах.

Умножение через интерполяцию

Но что, если бы мы могли вычислять значения в точках и делать интерполяцию быстрее? Выясняется, что это можно сделать, если рассматривать не произвольные точки, а только специальные — а именно, комплексные корни из единицы.

Корни из единицы

На комплексной плоскости эти числа располагаются на единичном круге на равном расстоянии друг от друга:

Все 9 комплексных корней степени 9 из единицы

Дискретное преобразование Фурье

Дискретным преобразованием Фурье собственно и называется вычисление значений многочлена в комплексных корнях из единицы:

Утверждение. Обратное ДПФ можно вычислить по формуле

$$ W^ <-1>= \dfrac 1 n \begin w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^ <-1>& w^ <-2>& w^ <-3>& \dots & w^ <1>\\ w^0 & w^ <-2>& w^ <-4>& w^ <-6>& \dots & w^ <2>\\ w^0 & w^ <-3>& w^ <-6>& w^ <-9>& \dots & w^ <3>\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^ <1>& w^ <2>& w^ <3>& \dots & w^ <-1>\end $$

Алгоритм

Напомним, что мы изначально хотели перемножать многочлены следующим алгоритмом:

В общем случае быстро посчитать интерполяцию и даже просто посчитать значения в точках нельзя, но для корней единицы — можно. Если научиться быстро считать значения в корнях и интерполировать (прямое и обратное преобразование Фурье), но мы сможем решить исходную задачу.

Схема Кули-Тьюки

Реализация

Приведём код, вычисляющий БПФ по схеме Кули-Тьюки:

При изначальном запуске следует дополнить массив до степени двойки:

Как обсуждалось ранее, обратное преобразование Фурье удобно выразить через прямое:

Оптимизированная версия

Попробуем избавиться от аллокаций вообще. Сейчас они происходят, потому что мы каждый раз разбиваем массив на два. Что произойдет, если вместо того, чтобы создавать новые массивы, просто сдвинуть все четные элементы в левую половину, а нечетные — в правую, и запуститься рекурсивно от половин?

Действительно, первой итерации все четные элементы (с нижним битом, равным нулю) будут записаны в первую половину (в позицию с верхним битом, равным нулю), а для нечетных наоборот. Дальше, все элементы со вторым самым младшим битом равным нулю будут внутри своих половин записаны в меньшую половину (со вторым самым старшим битом, равным нулю), и так далее.

Если мы знаем, где окажется каждый элемент, то давайте тогда даже не будем делать какие-либо перестановки внутри рекурсии, а просто выполним их один раз в самом начале, а в рекурсивной функции будем просто запускаться от половин.

У алгоритма довольно неплохая численная стабильность, однако в олимпиадных задачах часто требуется считать какой-нибудь большой целочисленный ответ, либо посчитать его по модулю. От этой проблемы однако можно избавиться.

Number-theoretic transform

Источник

Понимание алгоритма БПФ

Здравствуйте, друзья. Уже завтра стартует курс «Алгоритмы для разработчиков», а у нас остался один неопубликованный перевод. Собственно исправляемся и делимся с вами материалом. Поехали.

Быстрое преобразование Фурье (БПФ — англ. FFT) является одним из важнейших алгоритмов обработки сигналов и анализа данных. Я пользовался им годами, не имея формальных знаний в области компьютерных наук. Но на этой неделе мне пришло в голову, что я никогда не задавался вопросом, как БПФ так быстро вычисляет дискретное преобразование Фурье. Я стряхнул пыль со старой книги по алгоритмам, открыл ее, и с удовольствием прочитал об обманчиво простой вычислительной уловке, которую Дж. В. Кули и Джон Тьюки описали в своей классической работе 1965 года, посвященной этой теме.

Цель этого поста — окунуться в алгоритм БПФ Кули-Тьюки, объясняя симметрии, которые к нему приводят, и показать несколько простых реализаций на Python, применяющих теорию на практике. Я надеюсь, что это исследование даст специалистам по анализу данных, таким как я, более полную картину того, что происходит под капотом используемых нами алгоритмов.

Дискретное преобразование Фурье

БПФ — это быстрый алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за . ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:

Прямое дискретное преобразование Фурье (ДПФ):

Обратное дискретное преобразование Фурье (ОДПФ):

Преобразование из xn → Xk является переводом из конфигурационного пространства в пространство частотное и может быть очень полезным как для исследования спектра мощности сигнала, так и для преобразования определенных задач для более эффективного вычисления. Некоторые примеры этого в действии вы можете найти в главе 10 нашей будущей книги по астрономии и статистике, где также можно найти изображения и исходный код на Python. Пример использования БПФ для упрощения интегрирования сложных в противном случае дифференциальных уравнений смотрите в моем посте «Решение уравнения Шредингера в Python».

Из-за важности БПФ (далее может быть использовано равносильное FFT — Fast Fourier Transform) во многих областях Python содержит множество стандартных инструментов и оболочек для его вычисления. И NumPy, и SciPy имеют оболочки из чрезвычайно хорошо протестированной библиотеки FFTPACK, которые находятся в подмодулях numpy.fft и scipy.fftpack соответственно. Самый быстрый БПФ, о котором я знаю, находится в пакете FFTW, который также доступен в Python через пакет PyFFTW.

На данный момент, однако, давайте оставим эти реализации в стороне и зададимся вопросом, как мы можем вычислить БПФ в Python с нуля.

Вычисление дискретного преобразования Фурье

Для простоты мы будем касаться только прямого преобразования, поскольку обратное преобразование может быть реализовано очень похожим образом. Взглянув на приведенное выше выражение ДПФ (DFT), мы видим, что это не более чем прямолинейная линейная операция: умножение матрицы на вектор

с матрицей М, заданной

Имея это в виду, мы можем вычислить ДПФ с использованием простого умножения матрицы следующим образом:

Мы можем перепроверить результат, сравнив его со встроенной в numpy БПФ-функцией:

Просто чтобы подтвердить медлительность нашего алгоритма, мы можем сравнить время выполнения этих двух подходов:

Мы более чем в 1000 раз медленнее, что и следовало ожидать для такой упрощенной реализации. Но это не самое худшее. Для входного вектора длины N алгоритм БПФ масштабируется как , в то время как наш медленный алгоритм масштабируется как . Это означает, что для элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!

Так как же БПФ добивается такого ускорения? Ответ заключается в использовании симметрии.

Симметрии в дискретном преобразовании Фурье

Одним из наиболее важных инструментов в построении алгоритмов является использование симметрий задачи. Если вы можете аналитически показать, что одна часть проблемы просто связана с другой, вы можете вычислить подрезультат только один раз и сэкономить эти вычислительные затраты. Кули и Тьюки использовали именно этот подход при получении БПФ.
Мы начнем с вопроса о значении . Из нашего выражения выше:

где мы использовали тождество exp [2π i n] = 1, которое выполняется для любого целого числа n.

Последняя строка хорошо показывает свойство симметрии ДПФ:

для любого целого числа i. Как мы увидим ниже, эту симметрию можно использовать для гораздо более быстрого вычисления ДПФ.

ДПФ в БПФ: использование симметрии

Кули и Тьюки показали, что можно разделить вычисления БПФ на две меньшие части. Из определения ДПФ имеем:

Мы разделили одно дискретное преобразование Фурье на два слагаемых, которые сами по себе очень похожи на меньшие дискретные преобразования Фурье, одно на значения с нечетным номером и одно на значения с четным номером. Однако до сих пор мы не сохранили никаких вычислительных циклов. Каждый член состоит из (N / 2) ∗ N вычислений, всего .

Хитрость заключается в использовании симметрии в каждом из этих условий. Поскольку диапазон k равен 0≤k True

Сопоставим этот алгоритм с нашей медленной версией:
-In [6]:

Наш расчет быстрее чем прямая версия на порядок! Более того, наш рекурсивный алгоритм асимптотически : мы реализовали быстрое преобразование Фурье.

Обратите внимание, что мы все еще не приблизились к скорости встроенного алгоритма FFT в numpy, и этого следовало ожидать. Алгоритм FFTPACK, стоящий за fft numpy, — это реализация на Фортране, которая получила годы доработок и оптимизаций. Кроме того, наше решение NumPy включает в себя как рекурсию стека Python, так и выделение множества временных массивов, что увеличивает время вычислений.

Хорошая стратегия для ускорения кода при работе с Python / NumPy — по возможности векторизовать повторяющиеся вычисления. Это мы можем сделать — в процессе удалять наши рекурсивные вызовы функций, что сделает наш Python FFT еще более эффективным.

Обратите внимание, что в вышеупомянутой рекурсивной реализации FFT на самом низком уровне рекурсии мы выполняем N / 32 идентичных матрично-векторных произведений. Эффективность нашего алгоритма выиграет, если одновременно вычислить эти матрично-векторные произведения как единое матрично-матричное произведение. На каждом последующем уровне рекурсии мы также выполняем повторяющиеся операции, которые можно векторизовать. NumPy отлично справляется с такой операцией, и мы можем использовать этот факт для создания этой векторизованной версии быстрого преобразования Фурье:

Хотя алгоритм немного более непрозрачен, это просто перестановка операций, используемых в рекурсивной версии, с одним исключением: мы используем симметрию в вычислении коэффициентов и строим только половину массива. Опять же, мы подтверждаем, что наша функция дает правильный результат:

Поскольку наши алгоритмы становятся намного более эффективными, мы можем использовать больший массив для сравнения времени, оставляя DFT_slow :
In [9]:

Мы улучшили нашу реализацию еще на порядок! Сейчас мы находимся на расстоянии примерно в 10 раз от эталона FFTPACK, используя всего пару десятков строк чистого Python + NumPy. Хотя это все еще не соответствует в вычислительном отношении, с точки зрения читаемости версия Python намного превосходит исходный код FFTPACK, который вы можете просмотреть здесь.

Итак, как FFTPACK достигает этого последнего ускорения? Ну, в основном, это просто вопрос детальной бухгалтерии. FFTPACK тратит много времени на повторное использование любых промежуточных вычислений, которые можно использовать повторно. Наша клочковатая версия все еще включает в себя избыток выделения памяти и копирования; на низкоуровневом языке, таком как Fortran, легче контролировать и минимизировать использование памяти. Кроме того, алгоритм Кули-Тьюки можно расширить, чтобы использовать разбиения размером, отличным от 2 (то, что мы здесь реализовали, известно как БПФ Кули-Тьюки радикса по основе 2). Также могут быть использованы другие более сложные алгоритмы БПФ, в том числе принципиально отличные подходы, основанные на сверточных данных (см., Например, алгоритм Блюштейна и алгоритм Рейдера). Комбинация вышеупомянутых расширений и методов может привести к очень быстрым БПФ даже на массивах, размер которых не является степенью двойки.

Хотя функции на чистом Python, вероятно, бесполезны на практике, я надеюсь, что они преподнесли некоторую интуицию в том, что происходит на фоне анализа данных на основе FFT. Как специалисты по данным, мы можем справиться с реализацией «черного ящика» фундаментальных инструментов, созданных нашими более алгоритмически настроенными коллегами, но я твердо убежден, что чем больше у нас понимания о алгоритмах низкого уровня, которые мы применяем к нашим данным, тем лучшими практиками мы будем.

Этот пост был полностью написан в блокноте IPython. Полный блокнот можно скачать здесь или посмотреть статически здесь.

Многие могут заметить, что материал далеко не новый, но, как нам кажется, вполне актуальный. В общем пишите была ли статья полезной. Ждём ваши комментарии.

Источник